一、试除法求约数
主要思想:由于当n/a=b时,a和b都是n的约数,即约数总是成对出现,可以在一次循环中同时找到i和n/i两个约数,只需要循环n/i次就能找到所有约数。
例题:求一个数的所有约数,并将它们按大小排序。
vector<int> get_divisors(int n){
vector<int> res;
for(int i=1;i<=n/i;i++){//只循环n/i次
if(n%i==0){//找到约数
res.push_back(i);
if(n/i!=i) res.push_back(n/i);//存入与i成对的那个约数
}
}
sort(res.begin(),res.end());//排序
return res;
}二、约数个数
主要思想:将数n分解成 ![]() ,数n的所有约数个数即为
,数n的所有约数个数即为的所有组合个数,可以用公式
……
求得。而分解过程即为在求一个数的所有质因子(详见【算法基础14】)算法上稍加改动,在存储质因子的同时存储该质因子的幂。
例题:给出由n个数,求它们的乘积的约数个数。
#include<iostream>
#include<algorithm>
#include<vector>
#include<unordered_map>
using namespace std;
typedef long long LL;
int main(){
int n;
cin>>n;
unordered_map<int,int> primes;//用哈希图存储质因子和它对应的幂
while(n--){
int x;
cin>>x;
for(int i=2;i<=x/i;i++){//求质因子
while(x%i==0){
x/=i;
primes[i]++;//该p对应的a++
}
}
if(x>1) primes[x]++;//处理大于x/i的那个质因子
}
LL res=1;
for(auto prime:primes){
res=res*(prime.second+1);//代入公式计算
}
cout<<res<<endl;
return 0;
}三、约数的和
主要思想:由![]() ,约数之和即为
,约数之和即为的组合个数的和,可以j将约数之和分解成
。
例题:给出由n个数,求它们的乘积的约数之和。
#include<iostream>
#include<algorithm>
#include<vector>
#include<unordered_map>
using namespace std;
typedef long long LL;
int main(){
int n;
cin>>n;
unordered_map<int,int> primes;
while(n--){
int x;
cin>>x;
for(int i=2;i<=x/i;i++){//分解
while(x%i==0){
x/=i;
primes[i]++;
}
}
if(x>1) primes[x]++;
}
LL rsum=1;
for(auto prime:primes){
int p=prime.first,a=prime.second;//pi和ai
LL t=1;
while(a--) t=t*p+1;//循环a次后,得p0+p1+...+p6
sum=sum*t;
}
cout<<sum<<endl;
return 0;
}四、辗转相除法(欧几里得算法)求最大公约数
主要思想:求a和b的最大公约数可以转化为求b和a%b的最大公约数,不断递归转化到求a和0的最大公约数,则答案为a。
例题:给出两个数,求它们的最大公约数。
int gcd(int a,int b){
return b?gcd(b,a%b):a;//如果b不为0,则返回gcd(b,a%b),否则返回a
}五、扩展欧几里得算法
主要思想:由裴蜀定理(对于任意正整数a,b,一定存在非零整数x,y,使得ax+by=a和b的最大公约数。)求a和b的构造系数x,y。
推导过程:

代码实现:
int exgcd(int a,int b,int &x,int &y){
if(!b){
x=1,y=0;//b=0时,a*1+0=a
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;//由推导更新系数
return d;
}
应用:求解同余方程。同余方程可以转化为裴蜀定理的形式,只要b是a和m的最大公约数的倍数,则同余方程一定有解,代入扩展欧几里得算法,x*(b/d)%m即为同余方程的解。
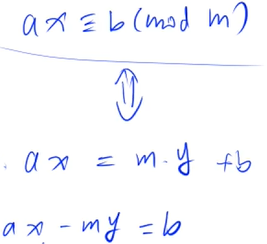
























 4639
4639

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








