众智科学：友谊悖论验证

万象穷究

已于 2022-10-29 10:50:21 修改

阅读量1.3k

点赞数 1

分类专栏：众智科学文章标签： c++ 学习

于 2022-10-29 10:45:37 首次发布

本文链接：https://blog.csdn.net/qq_52629381/article/details/127583895

版权

众智科学专栏收录该内容

3 篇文章

订阅专栏

实验内容：

输入：任意图的邻接矩阵（考察随机图和社会网络两种图，模拟生成）u

输出：符合友谊悖论的节点占比

相关定义：友谊悖论：是一种社会现象, 指大多数人认为, 自己的朋友比自己拥有更多的朋友

实验分析：

把友谊悖论的概念抽象到社会网络无向图G（V，E）中，其中V为图中的节点集，表示社交网络中的人；E为图中的边集，表示社交网络中的人际关系。两个人i与j是朋友当且仅当i，j∈V且(i，j)∈E, 即在图G中节点i和节点j之间存在边。定义d(v)为节点的度，即与它相连的节点个数，对应着表示一个人的朋友个数。

若图G中存在一个节点v满足友谊悖论，那么他的朋友的朋友比他自身的朋友要多。即d(v)比与它相邻节点的平均度数要小。

用数学公式表示为： $d(v)<\frac{\sum u\epsilon Vd(u)1E(u,v))}{d(v)}$ 。

其中，这里 $1E\left (u,v \right )$ 指示函数： $1A(x)=\left\{\begin{matrix} 1 &x\epsilon A \\ 0& else \end{matrix}\right.$

根据以上思路可以找到网络中满足友谊悖论的节点，再与网络中的总节点数相除，即可得到图中满足友谊悖论的节点比例R。

随机网络理论类似于社会网络结构，我们可以通过构建和刻画真正随机的网络来模拟社会的随机性。在实验过程中，生成多个随机网络并计算网络中满足友谊悖论的节点比例R，通过实验结果证明友谊悖论。

代码实现以及分析：

1.首先定义一个无向图类adjacencyWGraph:

属性：

方法：

adjacencyWGraph(int nV = 0, T theNoEdge = 0):构造方法，对属性进行初始化

void eraseEdge(int i, int j)：删除无向图的边(i,j)

void insertEdge(int v1, int v2, int weight)：插入边（v1,v2）

int degree(int theVertex) const:返回theVertex顶点的度数

bool existsEdge(int i, int j) const:判断(i,j)边是否已存在于无向图中

int* getEdges(int i)：返回与顶点i邻接的节点数组，即返回i点的朋友们

注：若输入了不在范围内的节点参数，则会报“非法插入”的错误

2.定义生成随机网络的方法：

思路：

1.图中有n个节点

2.选择一对节点，产生一个0-1之间的随机数。如果该随机数小于p，则这对节点之间放一条连接；否则，该节点对保持不连接。

3. 对所有N(N-1)/2个节点对重复步骤2。

通过随机网络的生成，会得到一个有n人，并且人与人之间成为朋友的概率为p的社会网络。

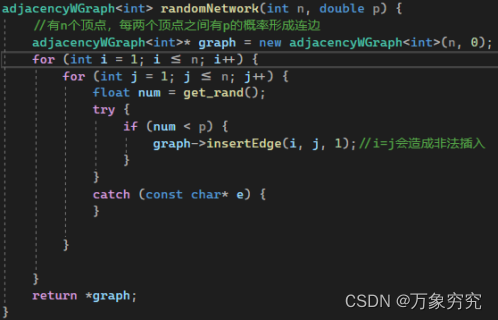
在以上生成随机网络的方法中，get_rand()是生成一个0-1的随机数的方法，思路如下：生成一个0-N的随机数，然后对其处以N+1，则可以得到0与1之间的浮点型随机数。N可以确定产生的精度。比如需要2位小数，则N=99,需要3位小数，则N=999。

代码如下：

3.定义计算在随机网络图graph中满足友谊悖论比例的函数：float R(adjacencyWGraph<int> graph)

思路如下：遍历图中所有节点，并通过无向图中定义的getEdges（i）的方法获得当前遍历节点i的朋友数组。计算出所有朋友的总度数再除以i的朋友总数获得i的朋友的平均朋友数avgdgree，接着用i的朋友数（即i的度数）与avgdgree比较，若dgree（i）<avgdgree即i点满足朋友悖论。遍历图中所有节点可得到满足悖论的节点总数，进而得到图中满足悖论的节点比例R。