暑假算法训练day2

原创于 2022-06-25 00:30:47 发布 · 250 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #位运算 #数据结构 #贪心算法 #构造算法

C++ 同时被 3 个专栏收录

221 篇文章

订阅专栏

算法

115 篇文章

订阅专栏

codeforces

42 篇文章

订阅专栏

本文讨论了两个不同问题：Alice和Bob在CoinRows游戏中如何最大化Bob的得分，以及如何构建Co-growingSequence以满足特定条件。前者通过枚举策略找到最优路径来限制Bob得分；后者关注字典序最小的序列生成，确保XOR操作后的数字满足特定规律。

C. Coin Rows

Alice 和 Bob 在一个 $\times m$ 的矩形上玩游戏，矩形的每一个格子上都有一个数 $a_{i,j}$
Alice 和 Bob 一开始站在左上角格子 (1,1) 上，每个人都只能向下或者向右移动，直到移动到终点 (2,m) 上，经过一个格子时会取走格子上的数，赢得相应的得分
Alice 首先开始移动，Bob 不能取走 Alice 已经取走的数
Alice 期望最小化 Bob 的得分，Bob 则希望最大化自己的得分
请输出 Bob 的最大得分
思路：
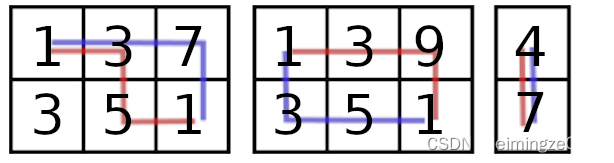
在这里插入图片描述
枚举每一列作为Alice向下走的那一步，那么Bob的得分只能是右上角和左下角Alice并未走过的分数，对每个Alice向下走的 $i$ ，求出Bob两种方式 $m a x$ ,再对所有 $m a x$ 求 $m i n$

#include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
const int N=1e5+10;
int a[3][N];
int s[3][N];
void solve()
{
	cin>>n;
	for(int i=1;i<=2;i++)
		for(int j=1;j<=n;j++)
			cin>>a[i][j];
	for(int i=1;i<=2;i++)
	{
		for(int j=1;j<=n;j++)
		{
			s[i][j]=s[i][j-1]+a[i][j];
		}
	}
	int res=ll_INF;
	for(int i=1;i<=n;i++)
	{
		int maxv=max(s[1][n]-s[1][i],s[2][i-1]);
		res=min(res,maxv);
	}
	cout<<res<<endl;
}
signed main()
{
    io;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}

D. Co-growing Sequence

题目描述：

思路：
字典序最小，那么 $b_1=0$ ，对于一个满足题意的数组，二进制下所有 $a_{i-1}XORb_{i-1}$ 中的 $1$ ， $a_{i}XORb_{i}$ 也得有，那么 $b_i$ 就是把没有补齐的 $1$ 补齐

#include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
const int N=2e5+10;
int a[N];
int b[N];
void solve()
{
	cin>>n;
	int now;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=2;i<=n;i++)
	{
		int t=a[i];
		now=a[i]|a[i-1];
		b[i]=now-t;
		a[i]^=b[i];
	}
	for(int i=1;i<=n;i++)cout<<b[i]<<' ';
	cout<<endl;
}
signed main()
{
    io;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}