回溯算法及其剪枝操作

1.回溯算法简介

在我们解决实际问题的时候，经常会遇到一种情况。即是我们现在面临很多种选择，我们需要先从中选择一个选项，然后基于这个选项又会派生出很多新的选项，接着重复这种操作，直到到达最终状态。

举一个经典的例子：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

这个问题又被称为n皇后问题。在构想具体的实现方法之前不如让我们现在棋盘上摆摆看。

由于8×8棋盘的情况过于复杂，所以笔者在这里使用4×4的棋盘来举例。

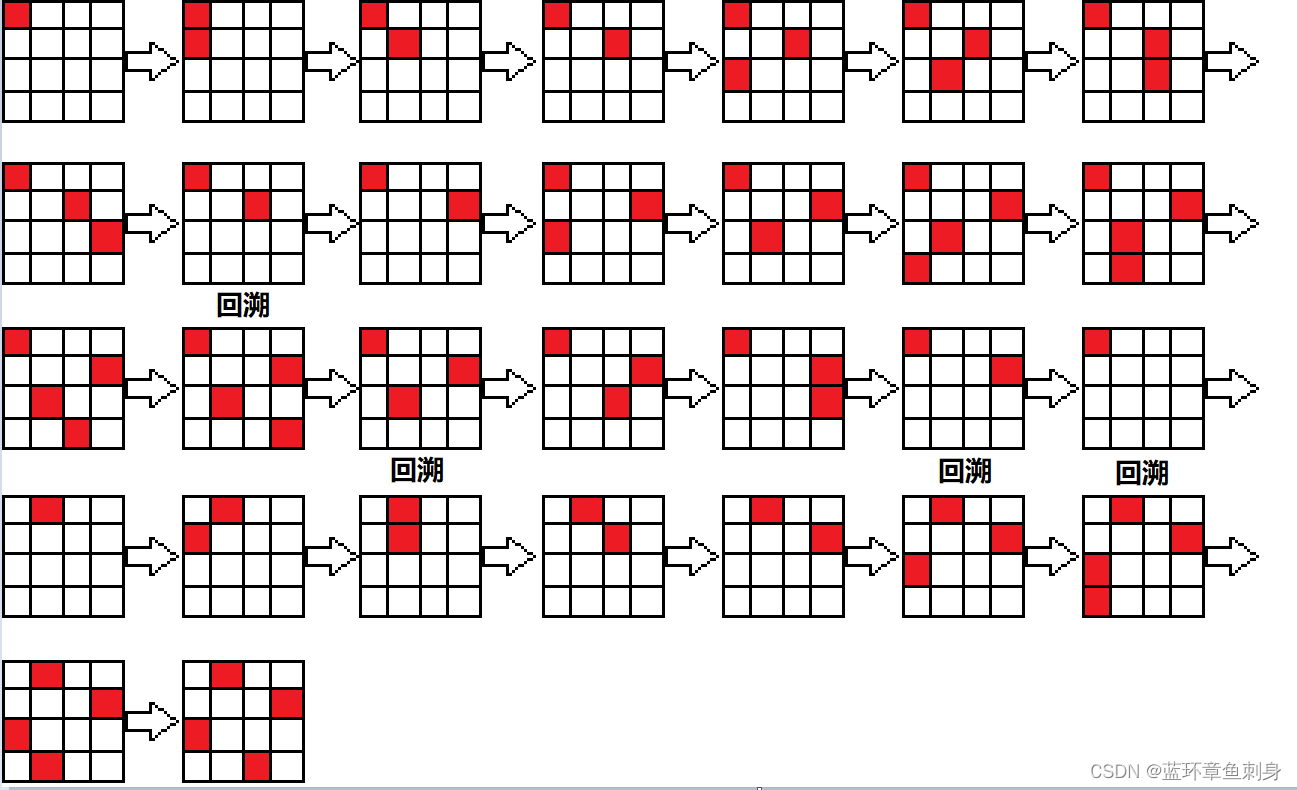
以下是对图中所做操作的文字描述：

在本例中，我们首先开始对第一行开始选位置，我们首先选择第一列。

接着我们开始对第二行的位置进行选择，由规则可知第一列与第二列并不符合要求。所以我们先选择第三列。

于是我们开始选择第三行了，通过对每一列的情况判断后我们发现没有一种情况能够满足我们的要求，于是我们决定将第二行的棋子拿起来，去寻找其他适合的位置。

接着我们选择放在第四列，并循环执行上述操作。

最后直到出现满足题目要求的情况时，我们便找到了一种符合要求的解法，如图最后的情况所示。

接着我们要继续循环下去，直至将棋盘上所有可能得摆法全部判断完，即可回答n皇后问题了。

上述操作中提到的把皇后棋子拿起来去寻找其他放置位置的操作被称为回溯，而基于以上思想实现的算法就被称之为回溯算法。

所以回溯算法的本质其实是一种暴力搜索算法，但是有些问题能够使用暴力搜索的方式解决就已经皆大欢喜了（笑）。所以为了简化我们的代码，我们可以使用递归函数的方式。接下来笔者将使用三个例题来讲解回溯算法的逻辑与具体使用。

 2.组合问题

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

首先先让我们来回忆一下排列与组合的定义。

排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

所以在考虑本题的时候，我们的考虑顺序应该是：

假设第一个元素取1，那么第二个元素可以依次取2、3、4。也就是[1,2],[1,3],[1,4]三种情况。

现在第二个元素没有新元素可取了，我们进行回溯。第一个元素取2，那么第二个元素可以依次取3、4（因为我们之前取过[1,2]的组合了，所以这里不能重复取1）。那么应该增加[2,3][2,4]两种情况。

同上，我们再进行一次回溯。并且增加[3,4]这种情况。

我们最后进行一次回溯，但是我们会发现当第一个元素取4的时候，第二个元素没有元素可以取。现在所以的情况都已经被我们遍历完了，所以我们得出了结果：满足条件的组合有[1,2],[1,3],[1,4],[2,3][2,4],[3,4]。

那么算法我们已经明确了，所以我们要怎样编写回溯算法的代码呢？

首先，我们可以把我们整个回溯的部分想象成一个树形结构，如下图所示。

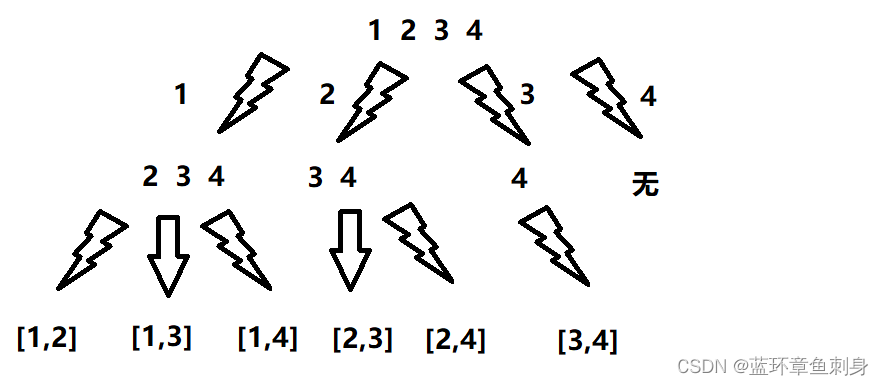
 在每一个树的分支处都可以想象成一次递归，而每次得出结果后都可以想象成一次回溯。由此，我们便对如何进行代码实现拥有了一个较为清楚的认识。

代码实现如下所示：

int* path;
int pathTop;
int** ans;
int ansTop;

void backtracking(int n,int k,int startIndex)
{
    //当path中元素个数为k个时，我们需要将path数组放入ans二维数组中
    if(k == pathTop)
    {
        //path数组为我们动态申请，若直接将其地址放入二维数组，
        //path数组中的值会随着我们回溯而逐渐变化
        //因此创建新的数组存储path中的值
        int* temp = (int*)malloc(sizeof(int) * k);
        int i = 0;
        for(i;i < k;i++)
        {
            temp[i] = path[i];
        }
        ans[ansTop++] = temp;
        return;
    }
    int j;
    for(j = startIndex;j <= n;j++)
    {
        //将当前结点放入path数组
        path[pathTop++] = j;
        //进行递归
        backtracking(n,k,j+1);
        //进行回溯，弹出数组最上层结点
        pathTop--;
    }
}

int** combine(int n, int k, int* returnSize, int** returnColumnSizes)
{
    //path数组用来存放可能的结果
    path = (int *)malloc(sizeof(int) * k);
    //ans二维数组用来存放符合条件的结果数的集合
    ans =(int **)malloc(sizeof(int*) * 10240); //指针数组
    pathTop = ansTop = 0;

    //回溯算法
    backtracking(n,k,1);
    //最后的返回大小为ans数组大小
    *returnSize = ansTop;
    //returnColumnSizes数组存储ans二维数组对应下标中一维数组的长度（都为k）
    *returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
    for(int i = 0;i < ansTop;i++)
    {
        (*returnColumnSizes)[i] = k;
    }
    free(path);

    return ans;
}

在此，笔者将继续对以上代码中的一些细节进行一些文字补充：

首先，path数组可以想象成一个用来暂时保存可能结果的栈。而ans指针数组用来存放结果。

Backtracking函数的三个参数分别为题目中给出的n和k，第三个参数表示当前这次递归应该把哪个数字放进path数组中。

而backtracking函数的终止条件为k==pathTop，即为递归的次数等于k。而下面的for循环则是遍历所有的可能性。在每次遍历的过程中，先将可能的元素进栈，然后继续递归。等递归返回后，进行退栈（这里其实就是回溯），将path数组恢复到递归之前的状态，再次进行下一次遍历。

由此我们便得出了所有可能得结果，并且保存在ans指针数组里面返回。

在这里，笔者将完全模拟一次递归调用的过程用来帮助还不太熟悉递归操作的读者更好的理解。在下文中，backtracking函数的第一次调用会使用红色，第二次调用使用紫色，第三次调用使用蓝色

首先我们的主调函数调用backtracking(n,k,1)。

此时的pathTop为0，递归继续。进入for循环，j=1，将1放入path数组的0号下标（1入栈），接着递归调用backtracking(n,k,2)。

此时pathTop为1，递归继续。进入for循环，j=2，将2放入path数组的1号下标，接着调用backtracking(n,k,3)。

此时pathTop为2，递归结束。将[1,2]放入ans数组，递归返回。

此时继续j=2循环中剩下的部分，进行退栈操作，将下标1（j=2）弹出栈，并且进行下次循环。此时j=3，将3放入path数组的1号下标，接着调用backtracking(n,k,4)。

此时pathTop为2，递归结束。将[1,3]放入ans数组，递归返回。

此时继续j=3循环中剩下的部分，进行退栈操作，将下标1（j=3）弹出栈，并且进行下次循环。此时j=4，将4放入path数组的1号下标，接着调用backtracking(n,k,5)。

此时pathTop为2，递归结束。将[1,4]放入ans数组，递归返回。

此时for循环结束，本次递归调用返回。

此时继续j=1循环中剩下的部分，进行退栈操作，将下标0（j=1）弹出栈，并且进行下次循环。此时j=2，将2放入path数组的0号下标，接着调用backtracking(n,k,2)。

此时pathTop为1，递归继续。进入for循环，j=3，将3放入path数组的1号下标，接着调用backtracking(n,k,4)。

此时pathTop为2，递归结束。将[2,3]放入ans数组，递归返回。

接下来将继续以上的调用过程，重复的过程笔者将不再赘述，直至所有的结果遍历结束，ans数组中存放的即是我们想要的所有结果。

组合问题的剪枝操作

当我们充分理解了以上的回溯算法时，我们会发现我们可能会进行一些无效操作，比如说当我们第一次调用backtracking时，for循环中j=4的情况，此时剩下的元素个数已经不能满足组成一个长度为2的数组了，所以这种遍历情况就会增大我们的时间开销。

为了避免这种情况，所以我们要进行剪枝操作。当我们把以上的递归调用过程全部想象成一棵树的时候，避免对这种情况的遍历就好像把树的树枝剪掉，这就是“剪枝”名字的由来。

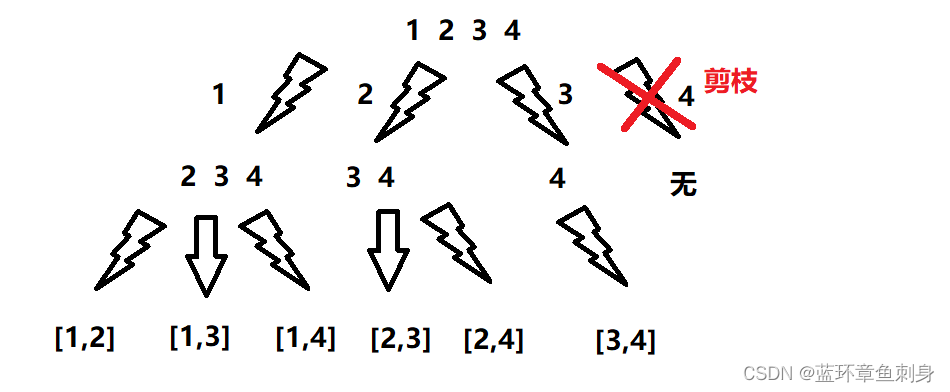
 对于本题的情况，我们只需要在for循环的判断条件中将"j <= n"修改为“j <= n - (k - pathTop) + 1”。

k - pathTop + 1的值为当前数组中还能容纳的元素个数（+ 1是因为数组下标从0开始）。所以通过这种判断就可以避免第一次循环中出现j =4的情况，从而提高了代码巡行的效率。

其实，我们在最开始编写代码的时候已经下意识地使用了剪枝的思想。因为当我们在第一次遍历的时候已经把不符合组合的情况排除出去了，这其实本身也是一种剪枝操作。被剪掉的树枝就是下图中红色方框中的数枝。

 至此，组合问题的回溯算法以及本算法的剪枝操作便全部介绍完了。

3.全排列问题

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

 由排列的性质我们可以得知，在全排列中每一个元素都要出现一次。

所以我们可以借用一个新数组help来存放每个元素是否出现过。若该元素没有出现过，help数组对应位置置0，反之置1。

由此我们就可以通过回溯help数组的形式来解决全排列的问题。

具体实现代码如下

int * path;
int pathTop;
int ** ans;
int ansTop;
int *help;

backtracking(int * nums,int numsSize)
{
    if(pathTop == numsSize)
    {
        int * temp = (int *)malloc(sizeof(int) * numsSize);
        for(int i = 0;i < numsSize;i++)
        {
            temp[i] = path[i];
        }
        ans[ansTop++] = temp;
        return;
    }
    for(int i = 0;i < numsSize;i++)
    {
        if(help[i] == 0)
        {
            path[pathTop++] = nums[i];
            help[i] = 1;
            backtracking(nums,numsSize);
            help[i] = 0;
            pathTop--;
        }
    }
}

int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes)
{
    path = (int *)malloc(sizeof(int) * numsSize);
    ans = (int **)malloc(sizeof(int **) * 10240);
    help = (int *)malloc(sizeof(int) * numsSize);
    pathTop = ansTop = 0;
    for(int i = 0;i < numsSize;i++)
    {
        help[i] = 0;
    }
   

    backtracking(nums,numsSize);
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
    for(int i = 0;i < ansTop;i++)
    {
        (*returnColumnSizes)[i] = numsSize;
    }

    free(path);
    free(help);
    return ans;
}

其实回溯算法的代码基本都是一个模板，在理解了组合问题之后相信各位读者也能够较为轻松地理解全排列的代码了。

笔者依然在这里模拟一次递归调用的过程来辅助一些理解困难的读者。

在下文中，backtracking函数的第一次调用会使用红色，第二次调用使用紫色，第三次调用使用蓝色，第四次调用使用绿色。

首先我们的主调函数调用backtracking。

此时的pathTop为0，递归继续。进入for循环，i=0，此时help[0]为0,path[0]置为1，同时把help[0]的值置为脏位（置为1），接着递归调用backtracking。

此时pathTop为1，递归继续。进入for循环，i=0，此时help[0]为1，循环结束。进入下次循环，i=1，help[1]=0，path[1]置为2，同时把help[1]的值置为脏位，接着调用backtracking。

此时pathTop为2，递归继续。进入for循环，i=0与i=1的情况下，此时help[i]为1，循环结束。进入下次循环，i=2，help[2]=0，path[2]置为3，同时把help[2]的值置为脏位，接着调用backtracking。

此时pathTop为3，递归结束。将[1,2,3]放入ans数组，递归返回。

此时继续i=2循环中剩下的部分，将help[2]回溯为0，并且进行退栈操作，将path[2]弹出栈，循环结束。

此时继续i=1循环中剩下的部分，将help[1]回溯为0，并且进行退栈操作，将path[1]弹出栈，循环结束。进入下次循环，i=2，help[2]=0，path[2]置为3，同时把help[2]的值置为脏位，接着调用backtracking。

此时pathTop为2，递归继续。进入for循环，i=0的情况下，此时help[0]为1，循环结束。进入下次循环，i=1，help[1]=0，path[2]置为2，同时把help[1]的值置为脏位，接着调用backtracking。

此时pathTop为3，递归结束。将[1,3,2]放入ans数组，递归返回。

此时继续i=1循环中剩下的部分，将help[1]回溯为0，并且进行退栈操作，将path[2]弹出栈，循环结束。进入下次循环，i=2，help[2]=1，循环结束。

此时继续i=2循环中剩下的部分，将help[2]回溯为0，并且进行退栈操作，将path[1]弹出栈，循环结束。

此时继续i=0循环中剩下的部分，将help[0]回溯为0，并且进行退栈操作，将path[0]弹出栈，循环结束。进入下次循环，i=1，此时help[1]为0，path[0]置为2，同时把help[1]的值置为脏位，接着调用backtracking。

此时pathTop为1，递归继续。进入for循环，i=0，help[0]=0，path[1]置为1，同时把help[0]的值置为脏位，接着调用backtracking。

此时pathTop为2，递归继续。进入for循环，i=0与i=1的情况下，此时help[i]为1，循环结束。进入下次循环，i=2，help[2]=0，path[2]置为3，同时把help[2]的值置为脏位，接着调用backtracking。

此时pathTop为3，递归结束。将[2,1,3]放入ans数组，递归返回。

接下来将继续以上的调用过程，重复的过程笔者将不再赘述，直至所有的结果遍历结束，ans数组中存放的即是我们想要的所有结果。

4.n皇后问题

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

n皇后问题的枚举思路在上文已做过完整介绍，此处不再重复。

n皇后问题的解决思路和上述两题类似，依然是基于递归与回溯。但是我们另需一个isValid函数来判断该中情况是否满足n皇后的条件并完成剪枝。

具体代码如下所示：

char ***ans;
char **path;
int ansTop, pathTop;
//将path中元素复制到ans中
void copyPath(int n) {
    char **tempPath = (char**)malloc(sizeof(char*) * pathTop);
    int i;
    for(i = 0; i < pathTop; ++i) {
        tempPath[i] = (char*)malloc(sizeof(char) * n + 1);
        int j;
        for(j = 0; j < n; ++j)
            tempPath[i][j] = path[i][j];
        tempPath[i][j] = '\0';

    }
    ans[ansTop++] = tempPath;
}

//判断当前位置是否有效（是否不被其它皇后影响）
int isValid(int x, int y, int n) {
    int i, j;
    //检查同一行以及同一列是否有效
    for(i = 0; i < n; ++i) {
        if(path[y][i] == 'Q' || path[i][x] == 'Q')
            return 0;
    }
    //下面两个for循环检查斜角45度是否有效
    i = y - 1;
    j = x - 1;
    while(i >= 0 && j >= 0) {
        if(path[i][j] == 'Q')
            return 0;
        --i, --j;
    }

    i = y + 1;
    j = x + 1;
    while(i < n && j < n) {
        if(path[i][j] == 'Q')
            return 0;
        ++i, ++j;
    }

    //下面两个for循环检查135度是否有效
    i = y - 1;
    j = x + 1;
    while(i >= 0 && j < n) {
        if(path[i][j] == 'Q')
            return 0;
        --i, ++j;
    }

    i = y + 1;
    j = x -1;
    while(j >= 0 && i < n) {
        if(path[i][j] == 'Q')
            return 0;
        ++i, --j;
    }
    return 1;
}

void backTracking(int n, int depth) {
    //若path中有四个元素，将其拷贝到ans中。从当前层返回
    if(pathTop == n) {
        copyPath(n);
        return;
    }

    //遍历横向棋盘
    int i;
    for(i = 0; i < n; ++i) {
        //若当前位置有效
        if(isValid(i, depth, n)) {
            //在当前位置放置皇后
            path[depth][i] = 'Q';
            //path中元素数量+1
            ++pathTop;

            backTracking(n, depth + 1);
            //进行回溯
            path[depth][i] = '.';
            //path中元素数量-1
            --pathTop;
        }
    }
}

//初始化存储char*数组path，将path中所有元素设为'.'
void initPath(int n) {
    int i, j;
    for(i = 0; i < n; i++) {
        //为path中每个char*开辟空间
        path[i] = (char*)malloc(sizeof(char) * n + 1);
        //将path中所有字符设为'.'
        for(j = 0; j < n; j++)
            path[i][j] = '.';
        //在每个字符串结尾加入'\0'
        path[i][j] = '\0';
    }
}

char *** solveNQueens(int n, int* returnSize, int** returnColumnSizes){
    //初始化辅助变量
    ans = (char***)malloc(sizeof(char**) * 400);
    path = (char**)malloc(sizeof(char*) * n);
    ansTop = pathTop = 0;

    //初始化path数组
    initPath(n);
    backTracking(n, 0);

    //设置返回数组大小
    *returnSize = ansTop;
    int i; 
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    for(i = 0; i < ansTop; ++i) {
        (*returnColumnSizes)[i] = n;
    }
    return ans;
}

5.总结

由上面三道例题我们可以得出一个结论：所有的回溯都是基于递归实现的。所以在使用递归函数解决问题的时候就可以想一想是不是可以使用回溯法解决问题。

回溯法是一种暴力搜索的方法，时间复杂度较高。但是我们可以使用剪枝的方法来适当降低时间开销，对于如何编写剪枝条件也就成了如何优化回溯算法性能的关键。

在此附上回溯算法的模版：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

最后，感谢@代码随想录的文章以及视频教程对笔者学习回溯算法起到了很大的帮助，在此附上本文的参考链接：

文章：代码随想录

视频课：带你学透回溯算法（理论篇）| 回溯法精讲！_哔哩哔哩_bilibili

同名文章发表于微信苏嵌教育公众号：回溯算法及其剪枝操作 (qq.com)