Leetcode刷题Python之1547.切棍子的最小成本-CSDN博客

本文链接：https://blog.csdn.net/qq_53086905/article/details/143692818

提示：使用动态规划的方法。

文章目录

一、题目描述
二、解题思路
三、代码实现
- 代码解析
总结

一、题目描述

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：
在这里插入图片描述
给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割，也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。
返回切棍子的最小总成本。

示例一：
在这里插入图片描述

输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

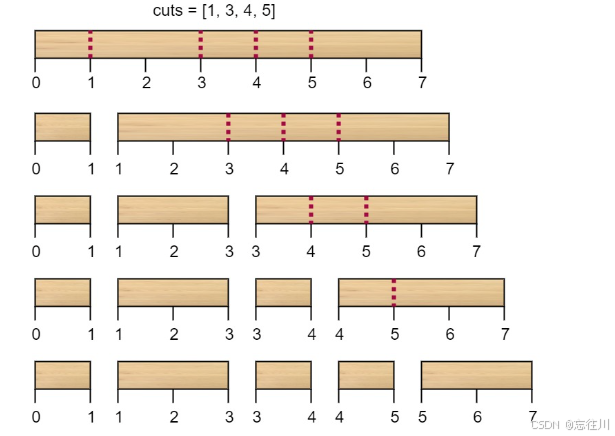
在这里插入图片描述
第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例二：

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

二、解题思路

这种优化类的问题很适合使用动态规划。下面我们逐步分析这个问题的动态规划解法。
第一步：重新定义 cuts 数组
在开始计算之前，为了简化问题，我们先将木棍的左右端点 0 和 n 也加入到 cuts 数组中，然后对 cuts 数组排序。这样，cuts 数组变为一个包含所有切割点和边界的有序数组。

例如，对于 n = 7, cuts = [1, 3, 4, 5]，我们可以将 cuts 转化为 [0, 1, 3, 4, 5, 7]。通过这种方式，我们可以更方便地计算木棍每段的长度。

第二步：构建 DP 状态转移表
1.定义 DP 状态：设 dp[i][j] 表示在切割点 cuts[i] 和 cuts[j] 之间切割的最小成本。

2.状态转移方程：
在 cuts[i] 和 cuts[j] 之间选择一个切割点 cuts[k]，我们将区间分为 [cuts[i], cuts[k]] 和 [cuts[k], cuts[j]] 两部分。
切割的成本是当前区间的长度 cuts[j] - cuts[i] 加上将左右两部分递归切割的最小成本 dp[i][k] 和 dp[k][j]。
综合得出状态转移方程：
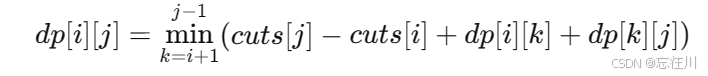
在这里插入图片描述
3.初始化：当 j - i < 2 时，即当区间长度小于 2 时，不需要切割，dp[i][j] = 0。

4.填表顺序：由于 dp[i][j] 依赖于更小的区间结果，我们采用自底向上、先短后长的顺序填表。

三、代码实现

代码如下：

class Solution(object):
    def minCost(self, n, cuts):
        """
        :type n: int
        :type cuts: List[int]
        :rtype: int
        """
        # 将 0 和 n 也加到 cuts 数组中，并排序
        cuts = sorted(cuts + [0, n])
        m = len(cuts)
        
        # 初始化 DP 表
        dp = [[0] * m for _ in range(m)]
        
        # 计算最小切割成本
        for length in range(2, m):  # 区间长度从2开始
            for i in range(m - length):
                j = i + length
                dp[i][j] = float('inf')
                
                # 尝试在区间内选择切割点 k
                for k in range(i + 1, j):
                    cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]
                    dp[i][j] = min(dp[i][j], cost)
        
        # 最终结果是从 0 到 n 的最小切割成本
        return dp[0][m - 1]