区间操作：线段树，珂朵莉树，树状数组

胃口很大的一条小蛇仔

已于 2022-05-11 18:24:37 修改

阅读量534

点赞数

分类专栏：数据结构文章标签：数据结构

于 2022-05-05 21:48:00 首次发布

本文链接：https://blog.csdn.net/qq_53133234/article/details/124593044

版权

数据结构专栏收录该内容

1 篇文章 0 订阅

订阅专栏

一般来说，区间的操作都可以用for循环来完成，但是当数据足够大时，在规定的时间内就极有可能超时，所以利用这三种数据结构，可以极大地减少时间复杂度。

一.线段树

1.简介：

线段树上的每个节点都维护一个区间。根维护的是整个区间，子节点维护的是父节点区间二等分后的其中一个子区间

2.功能：

区间修改，区间查询（区间求和，求区间最大值，求区间最小值）

有个大小为5的数组a=[10,11,12,13,14] ，将其转化为线段树，如图所示

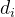${d_{i}}^{}$ 保存的是区间上所有数的和

d1所管辖的区间是[1,5]即a1,a2,a3,a4,a5，d1所保存的是a1+a2+a3+a4+a5即60

${d_{i}}^{}$ 的左儿子节点是 ${d_{2i}}^{}$ ，右儿子节点是 ${d_{2i+1}}^{}$

${d_{i}}^{}$ 表示的区间是[s,t]，那么 ${d_{i}}^{}$ 的左儿子节点表示的区间是[s， $\frac{s+t}{2}$ ]，右儿子节点表示的区间是[ $\frac{s+t}{2}+1$ ，t]

构建线段树：

int a[] = {10,11,12,13,14};
//如果数组有n个数需要转换为线段树，那么数组的长度设为4*n
int d[5*4];
void build(int s,int t,int p){
	//对[s,t]区间建立线段树,p为当前结点的编号 
	if(s == t){//到达叶子节点，赋值 
		d[p] = a[s];
		return;
	} 
	int m = s + ((t-s)>>1);
	//递归对左右区间建树 
	build(s,m,p * 2);
	build(m + 1,t,p * 2 + 1);
	d[p] = d[p * 2] + d[p * 2 + 1];
}

区间查询：

仍然以最开始的图为例，如果要查询区间[1,5]的和，那直接获取d[1]的值（60）即可。

如果要查询的区间为[3,5]，此时就不能直接获取区间的值，但是[3,5]可以拆成[3,3]和[4,5]，可以通过合并这两个区间的答案来求得这个区间的答案。

一般地，如果要查询的区间是 [l,r]，则可以将其拆成最多为多个极大的区间，合并这些区间即可求出[l,r]的答案。

代码：

int getsum(int l,int r,int s,int t,int p){
	//[l,r]为查询区间，[s,t]为当前节点包含的区间，p为当前节点的编号
	if (l <= s && t <= r){//当前区间为询问区间的子集 
		return d[p];
	} 
	int m = s + ((t-s)>>1),sum = 0;
	if(l <= m){//如果左儿子代表的区间[l,m]与询问区间有交集，则递归查询左儿子 
		sum += getsum(l,r,s,m,p*2);
	}
	if(r > m){//如果右儿子代表的区间[m+1,t]与查询区间有交集，则递归查询右儿子 
		sum += getsum(l,r,m+1,t,p*2+1);
	}
	return sum;
}

代码解析：

假设l = 3，r = 5，s = 1，t = 5，上面的代码是如何运转的呢？

首先判断[1,5]并不是[3,5]的子集，往下走，将当前区间的范围缩小，缩小为[1,3]和[4,5]两个区间

[1,3]区间与[3,5]区间有交集，递归查询，此时s = 1，t = 3

[1,3]不是[3,5]的子集，与上同理，当前区间缩小为[1,2]和[3,3]两个区间

[3,3]是[3,5]的子集，返回节点5的值，[1,2]继续往下走，到最后不会返回任何东西。

区间修改与懒散标记：

为什么要引入懒散标记？懒散标记在什么时候有用？

试想，如果我们在操作的时候，首先进行区间修改，修改了800次，然后再进行一次查询。这样，如果我们每次都将整个线段树的数据进行更新，实际上是非常慢的，如果我们能用一段空间，来记录修改数据，只有在使用的时候，一次性更新，就非常的方便。这样我们就引入了懒散标记。如果修改一次查询一次，修改一次查询一次，那就完全没有不要使用懒散标记，不仅耗费了空间还耗费了时间。

【懒散标记】：暂时不修改子节点的信息。先更新所有父节点的信息并在父节点这记录修改数据，等到下次访问子节点时再利用标记修改子节点的信息，使查询结果依旧准确

总之，就是不使用的时候就一直积累着，在使用的时候再统一更新。

例：我们要给区间[3,5]中的每个数都加上5，根据上面的分析，我们知道它可以分解为两个极大区间[3,3]和[4,5](分别对应节点3和节点5)

我们直接在这两个节点上进行修改，并给他们打上标记

3号节点的两个子节点不更新，等到我们要查询这两个子节点的信息时，标记下放，再给他们加上

现在，我们要查询区间[4,4]的各数字和

我们通过递归找到[4,5]区间，发现该区间上存在懒散标记。这时候就到标记下放的时间了。我们将该区间的两个子区间的信息更新，并清除该区间上的标记。

这里我们设懒散标记数组为t，如果t[p](p为当前结点的编号)存在值，就说明我在使用这个结点，而这个时候我就要下放更新数据了。

//更新积累的值 
void push_down(int s,int t,int p){
	int m = s + ((t - s) >> 1);
	if(t[p]){//如果当前节点的懒散标记非空，那么更新下面的子节点
		d[p * 2] += t[p] * (m - s + 1);
		d[p * 2 + 1] += t[p] * (t - m);
		//将标记下传给子节点（儿子接力父亲） 
		t[p * 2] += t[p];
		t[p * 2 + 1] += t[p];
		//清空当前节点的标记 
		t[p] = 0; 
	}
}

接下来给出在存在标记的情况下，区间修改和查询操作的参考实现。

区间修改（区间加/减上某个值）：

void update(int l,int r,int c,int s,int t,int p){
	//[l,r]为修改区间，c为变化量，[s,t]为当前节点的区间，p为当前节点的编号 
	if(l <= s && t <= r){
		//如果找到了目标区间，修改节点的值并打上懒散标记 
		d[p] += (t - s + 1) * c;
        t[p] += c; 
		return;
	}
    push_down(s,t,p);
	int m = s + ((t - s) >> 1);
	if(l <= m){
		update(l,r,c,s,m,p*2);
	}
	if(r > m){
		update(l,r,c,m+1,t,p*2+1);
	}
	d[p] = d[p*2] + d[p*2+1];
}

区间求和：

int getsum(int l,int r,int s,int t,int p){
	//[l,r]为查询区间，[s,t]为当前节点包含的区间，p为当前节点的编号
	if (l <= s && t <= r){//当前区间为询问区间的子集 
		return d[p];
	} 
	push_down(s,t,p);
	int m = s + ((t-s)>>1),sum = 0;
	if(l <= m){//如果左儿子代表的区间[l,m]与询问区间有交集，则递归查询左儿子 
		sum += getsum(l,r,s,m,p * 2);
	}
	if(r > m){//如果右儿子代表的区间[m+1,t]与查询区间有交集，则递归查询右儿子 
		sum += getsum(l,r,m + 1,t,p * 2 + 1);
	}
	return sum;
}

当区间修改为某一个值而不是修改某一个值：

void update(int l,int r,int c,int s,int t,int p){
	//[l,r]为修改区间，c为变化量，[s,t]为当前节点的区间，p为当前节点的编号 
	if(l <= s && t <= r){
		//如果找到了目标区间，修改节点的值并打上懒散标记 
		d[p] = (t - s + 1) * c,t[p] = c; 
		return;
	}
    push_down(s,t,p);
	int m = s + ((t - s) >> 1);
	if(l <= m){
		update(l,r,c,s,m,p*2);
	}
	if(r > m){
		update(l,r,c,m+1,t,p*2+1);
	}
	d[p] = d[p*2] + d[p*2+1];
} 

int getsum(int l,int r,int s,int t,int p){
	//[l,r]为查询区间，[s,t]为当前节点包含的区间，p为当前节点的编号
	if (l <= s && t <= r){//当前区间为询问区间的子集 
		return d[p];
	} 
    push_down(s,t,p);
	int m = s + ((t-s)>>1),sum = 0;
	if(l <= m){//如果左儿子代表的区间[l,m]与询问区间有交集，则递归查询左儿子 
		sum += getsum(l,r,s,m,p * 2);
	}
	if(r > m){//如果右儿子代表的区间[m+1,t]与查询区间有交集，则递归查询右儿子 
		sum += getsum(l,r,m + 1,t,p * 2 + 1);
	}
	return sum;
}

那如果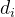 ${d_{i}}^{}$ 保存的是区间的最值，又是怎么操作的呢？

void build(int s,int t,int p){
	//对[s,t]区间建立线段树，当前根的编号为p 
	if(s == t){
		d[p] = a[s];
		return;
	} 
	int m = s + ((t-s)>>1);
	//递归对左右区间建树 
	build(s,m,p*2),build(m+1,t,p*2+1);
    //根据左右儿子的值，选择两个当中大的那一个，更新自己（依次向上更新）
	d[p] = std::max(d[p * 2],d[p * 2 + 1]);
} 

void update(int l,int r,int c,int s,int t,int p){
	//[l,r]为修改区间，c为变化量，[s,t]为当前节点的区间，p为当前节点的编号 
	if(l <= s && t <= r){
		//如果找到了目标区间，修改节点的值并打上懒散标记 
		d[p] = (t - s + 1) * c;
        t[p] = c; 
		return;
	}
    push_down(s,t,p);
	int m = s + ((t - s) >> 1);
	if(l <= m){
		update(l,r,c,s,m,p*2);
	}
	if(r > m){
		update(l,r,c,m+1,t,p*2+1);
	}
 	d[p] = std::max(d[p * 2],d[p * 2 + 1]);
}

int query(int l,int r,int s,int t,int p){
	if(l <= s && t <= r){
		return d[p];
	}
	push_down(s,t,p);
	int m = s + ((t - s) >> 1),ans = 0;
	if(s <= m){
		ans = std::max(ans,query(l,r,s,m,p * 2));
	}
	if(r < m){
		ans = std::max(ans,query(l,r,m + 1,t,p * 2 + 1));
	}
	return ans;
}

二.珂朵莉树

1.简介

通过set存放若干个用结构体表示的区间，每个区间的元素都是相同的。

2.功能

只要是涉及区间赋值操作的题，都可以用珂朵莉树处理任何关于区间信息的询问。

注意：（对区间必须要有赋值操作才能用珂朵莉树）！！！

构造：

struct node{
	int l,r;//区间的左右边界
	mutable bool v;//区间内的数值的类型 
	node(int L,int R = -1,bool V = false):l(L),r(R),v(V) {}
	inline bool operator<(const node& o) const{
		return l < o.l;
	}
};

为了方便，我们使用宏定义：#define IT set<node>::iterator

核心操作：split（）分解函数

从set中的所有区间中找到pos所在区间[l,r]，拆成两个区间，一个是[l,pos)，另一个是[pos,r]

主要目的是：使pos作为一个区间的开头，并返回这个区间的迭代器函数

步骤：

查找set中第一个>=pos的结点，如果找到的结点的左边界刚好是pos，则直接返回指向该节点的迭代器，如果不是，说明pos包含在前一个结点所在的区间，此时便删除pos所在的结点，然后以pos为分界点，将此结点分裂成两个结点分别插入set中，并返回后一个结点的迭代器。

IT split(int pos){
	//二分查找pos所在的区间 
	IT it = s.lower_bound(node(pos)); 
	if(it != s.end() && it->l == pos){
		//如果找到了pos所在的区间，并且区间的左边界刚好是pos，直接返回 
		return it;
	}
	--it;//如果没找到，则说明他在前面的区间 
	int L = it->l,R = it->r,V = it->v;
	s.erase(it);//先删除[L,R) 
	s.insert(node(L,pos-1,V));//插入[L,pos)
	return s.insert(node(pos,R,V)).first;//插入[pos,R)并返回地址 
}

另一个核心操作：assign（）合并函数

将值相同的区间合并成一个结点存入set

主要目的是：将一个区间[l,r]全部设定为某个值

步骤:

获取l的迭代器itl，和r的迭代器itr，删除从itl到itr的全部元素，再插入一个新的结点Node{l,r,v}

void assign(int l,int r,bool v){
	IT itr = split(r+1),itl = split(l);
	s.erase(itl,itr);
	s.insert(node(l,r,v));
}

注意：在分裂区间的时候一定要先右后左！！！

其他操作：

通用方法是先split出itr，再split出itl，然后直接暴力扫描这段区间内的所有结点，执行需要的操作。

例：求区间和

int queint querySum(int l,int r){
	int res = 0;
	IT itr = split(r+1),itl = split(l);
	for(IT it = itl;it != itr; ++it){//it就代表一个区间 
		res += (it->r - it->l + 1) * it->v;
	}
	return res;
}

三.树状数组

1.简介

树状数组天生用来维护数组的前缀和，从而快速求得某一区间的和，并支持对元素的值进行修改，记住，所有的区间求值都可以转化成用sum[m]-sum[n-1]来表示

树状数组的工作原理：

上面的黑色的8个方块就表示数组a。红色的8个方块就代表数组c

c[1] = a[1]

c[2] = a[1]+a[2]

c[3] = a[3]

c[4] = a[1]+a[2]+a[3]+a[4]

c[5] = a[5]

c[6] = a[5]+a[6]

c[7] = a[7]

c[8] = a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]

c就相当于a的上级，每个c组的成员都管理着不同数量的a组成员

那么问题来了，我们怎么知道ci管理的是数组a中的哪个区间呢？

这时我们引入一个函数：lowbit()

int lowbit(int x){
	return x&(-x);//-x = ~x+1(每位取反末尾加1)
}

举例：

c[6] = a[5]+a[6]

${(6)_{10}}^{}$ = ${(110)_{2}}^{}$ ，第一个‘1’对应的十进制是2，所以它要存储2个元素

c[8] = a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]

${(8)_{10}}^{}$ = ${(1000)_{2}}^{}$ ，第一个‘1’对应的十进制为8，所以它要存储8个元素

单点修改&区间查询：

单点修改：

操作：将 ${a_{x}}^{}$ 加上k，只需要更新 ${a_{x}}^{}$ 的所有上级

void update(int x,int k){
	while(x <= n){
		c[x] += k;
		x += lowbit(x);
	}
}

代码说明：

x = 6，k = 1

c[6] = 1

x = 8

c[8] = 1

x = 9（x > n）结束循环

前缀求和：

void getSum(int x){//a1+a2+……+ax
	int ans = 0;
	while(x >= 1){
		ans += c[x];
		x -= lowbit(x);
	}
	return ans;
}

代码说明：

x = 6

ans += c[6] // c[6] = a[6]+a[5]

x = 4

ans += c[4] // c[4] = c[1]+c[2]+c[3]+c[4]

x = 0 （x < 1）结束循环

区间查询：

int sum = getSum(m) - getSum(n-1); //区间[n,m]上值的和等于sum[m]-sum[n-1]

区间修改&单点查询

为了化简时间复杂度，我们将区间修好变成单点修改，这就需要引入差分的概念。

差分：

a是原数组，b是差分数组

//根据定义可知
b[i] = a[i] - a[i-1];

b[1] = a[1];
b[2] = a[2] - a[1];
b[3] = a[3] - a[2];
...
b[i] = a[i] - a[i-1];

//转化一下，求数组b的前缀和,根据上面公式可得
b[1]+b[2]+b[3]+...+b[i]
= a[1]+(a[2]-a[1])+(a[3]-a[2])+...+(a[i]-a[i-1])
= a[i]

//由此可知，原序列为差分序列的前缀和序列，即 ${a_{i}}^{} = \sum_{j=1}^{i}{b_{i}}^{}$

例如：

a = [1,2,3,5,6,9]

b = [1,1,1,2,1,3]

如果我们把[2,5]区间内的值都加上2，则变成

a = [1,4,5,7,8,9]

b = [1,3,1,2,1,1]

我们发现，当区间[x,y]中的值改变，除了b[x]和b[y+1]之外其余在区间内的差值是不变的。利用这个性质对b建立树状数组(也就是不再对原数组a建立树状数组，改成利用a的差分数组b来建立树状数组)。这样我们就将要更新一个区间的值变成只需要更新两个点

for(int i = 1;i <= n;i++){
	cin >> a[i];
	update(i,a[i]-a[i-1]);//在输入a数组的时候就将其改为差分数组 
}
//修改b[x]和b[y+1] 
update(x,k);
update(y+1,-k);
//查询ai
int a = getSum(i);

区间修改&区间查询

我们还是利用差分求r的前缀和

$\sum_{i=1}^{r}{a_{i}}^{} = \sum_{i=1}^{r}\sum_{j=1}^{i}{b_{i}}^{}$

a[1]+a[2]+a[3]+……+a[r]

=b[1] + (b[1]+b[2]) +…… + (b[1]+b[2]+……+b[r])

=r*b[1] + (r-1)*b[2] +……+b[r]

=r*(b[1]+b[2]+……+b[r]) - (0*b[1]+1*b[2]+2*b[3]+……+(n-1)*b[n])

上式就变成了： $\sum_{i=1}^{r} {a_{i}}^{} = r*\sum_{j=1}^{r}{b_{i}}^{} - \sum_{j=1}^{r}{(i-1)*b_{i}}^{}$

需要维护两个树状数组sum1[i] = b[i]，sum2[i] = (i-1)*b[i]

int a[MAXN];
int sum1[MAXN],sum2[MAXN];
void update(int i,int k){
	int x = i;
	while(i <= n){
		sum1[i] += k;
		sum2[i] += (x-1) * k;
		i += lowbit(i);
	}
}
int getSum(int i){
	int ans = 0,x = i;
	while(i >= 1){
		ans += x * sum1[i] - sum2[i];
		i -= lowbit(i);
	}
	return ans;
}

int main(){
	cin >> n;
	for(int i = 1;i <= n;i++){
		cin >> a[i];
		update(i,a[i]-a[i-1]);
	}
	update(x,k);
	update(y+1,-k);
	//[x,y]的区间和 
	int sum = getSum(y) - getSum(x-1);
	return 0;
}