线段树（简单实现高效区间操作）

以“前缀和”及“差分”作为引入

——问题A——
假设现在有长度为$n$的序列$a$，和$m$个问题，
每一个问题包含一个区间的左端点和右端点，要求得出这个区间段所有元素的总和。
（其中$n<=1e6,m<=1e6$）

解决思路：
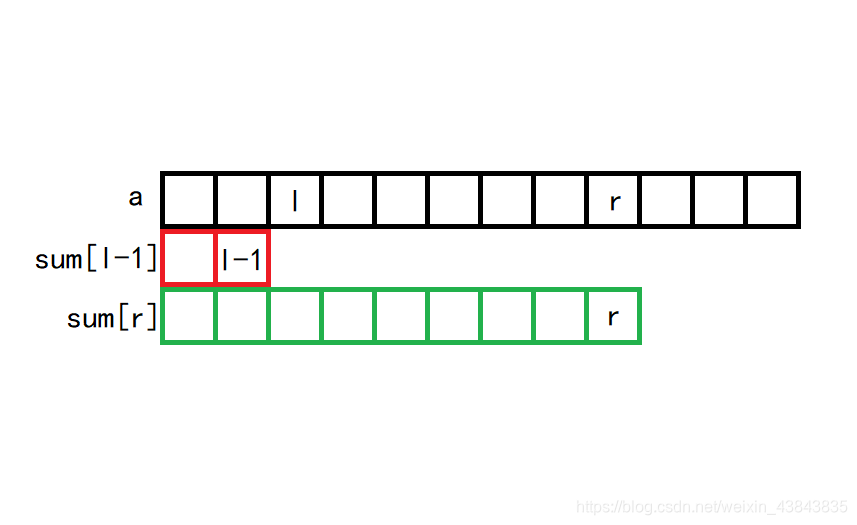
显然对于每一个提问都进行一次遍历累加必定会超时，最坏可达到$1e6\ast 1e6$。假设区间左端点为$l$，右端点为$r$，如果我们已经知道前$l-1$项的和$sum[l-1]$以及前$r$项的和$sum[r]$，那么答案即为$sum[r]-sum[l-1]$，这样的查询区间和操作的时间复杂度即为$O(1)$。完成这一前置操作也十分简单，在读入数据时，就可以利用递推式$sum[i]=sum[i-1]+a[i]$，得出从第$1$项到第$i$项的和。这样的思想及其方法称为 前缀和。

——问题B——
假设现在有长度为$n$的序列$a$，和$m$个问题，
每个问题给出一个区间的左端点和右端点，和一个$d$，表示对这个区间的所有元素都加上$d$。
$m$个问题结束后，输出这个序列。
（其中$n<=1e6,m<=1e6$）

解决思路：
暴力是万能的，超时是显然的。面对这个数据量，千万不能每次都老老实实的对每一个区间元素都加上$d$。其实可以借助“导数”的知识轻松处理，对于一段要修改的区间，在区间头$l$的位置放入一个标记$d$，表示从这里开始每个元素加上$d$；同时，在区间尾$r+1$的位置放入一个标记$-d$，表示从这里开始后面的元素不用加$d$了。这样的标记是可以叠加以及交叉的，当把$2m$个标记都打完后，最后从左到右依次遍历序列中每个元素，对于$i$，修改为$a[i]+=su{m}_d[i]$。这样，区间修改的时间复杂度即为$O(1)$，这样的区间修改方法称为 差分。

——问题C——
假设现在有长度为$n$的序列$a$，和$m$个问题，问题有两种：
1.给出一个区间的左端点和右端点，和一个$d$，表示对这个区间的所有元素都加上$d$。
2.给出一个区间的左端点和右端点，输出当前这段区间所有元素的总和。
（其中$n<=1e6,m<=1e6$）

解决思路：
介绍了上面的前缀和以及差分，不难发现，这两者是互不相容的操作，无法同时满足$O(1)$的查询区间和以及$O(1)$时间的区间修改。无论选择上面的哪种策略，都只能快速解决其中一个问题，而另一个问题仍然需要近乎暴力的手法解决，最终仍然会面临超时的风险。那么是否有一种兼顾快速查询与快速修改的方法，较为折中的方法呢？答案是肯定的，而且很容易想到，这个高效的而且折中的方法一定会与二分($logn$)有关，它就是基于完美二叉树(Perfect Binary Tree) 实现的线段树。

线段树的概念及其对区间问题的处理

线段是是擅长处理区间的数据结构，基于完美二叉树实现，区间操作可以在$O(logn)$时间内完成，对于这棵树中的每一个结点，要么是叶子，要么是一颗有两个子结点的树。其结构如下：

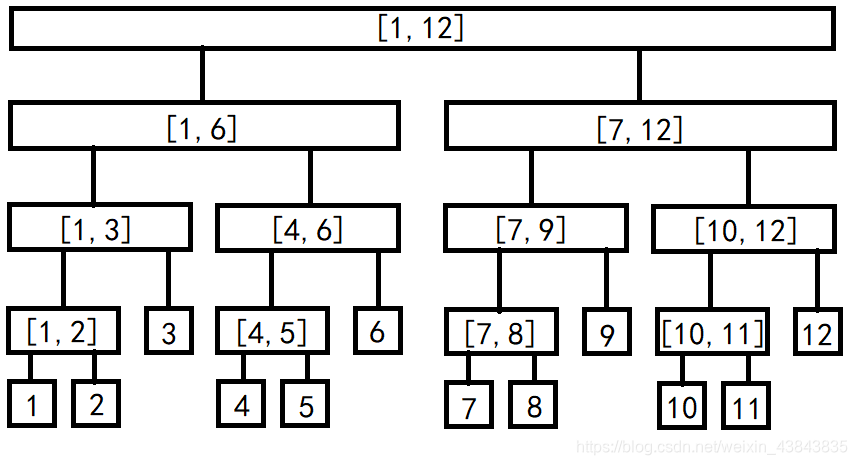
算法的本质就是用时间换空间，或用空间换时间。存储这样一棵线段树，对于长度为$n$的序列，需要至少$2n$的存储空间。通常情况下，为了防止操作时指针溢出，往往要开$4n$的存储空间。

——线段树的建立——
线段树可以用一个简单的一位数组实现，假设父节点为$i$，它的两个子结点分别存储在$2i$和$2i+1$的位置。对于一棵线段树，它的底层是原序列，上面的父节点可以根据题目需要填入合适的值。比如，我们可以用父节点存储它所指向区间的所有元素和，亦或是该区间的最小、最大元素。建立这些信息时，并不需要额外操作，在建立线段树时，即可一边回溯一边完成写入。

//常用父节点性质 
int pushup_sum(int p)//父节点存储区间元素和 
{
	return tree[p]=tree[p<<1]+tree[p<<1|1];
	//p为父节点，p<<1为左儿子，p<<1|1为右儿子 
} 
int pushup_min(int p)//父节点存储区间最小值 
{
	return tree[p]=min(tree[p<<1],tree[p<<1|1]);
} 
int pushup_max(int p)//父节点存储区间最大值 
{
	return tree[p]=max(tree[p<<1],tree[p<<1|1]);
}

线段树的建立基于递归的思想，自上而下的把区间划分成单个元素，再自下而上的逐步回溯写入父节点的性质。

//线段树的建立
void build_tree(int p,int l,int r)
{
	//递归到底层，该节点为叶节点，赋值，开始回溯
	if(l==r) 
	{
		tree[p]=a[l];
		return;
	}
	
	//二分递归，建立二叉树;
	int mid=(l+r)>>1;
	build_tree(p<<1,l,mid);
	build_tree(p<<1|1,mid+1,r);
	
	//依据需要的性质写入父节点，上面提供了三种常用的性质 
	pushup_sum(p); 
} 

——区间问题1——
查询区间$[l,r]$中所有元素的和。

根据线段树的结构，我们还是使用递归分块的思路自下而上逐步组成我们需要的元素和。

//查询区间和 
int RMQ_sum(int lq,int rq,int l,int r,int p)
{
	int ans=0;
	//如果问题区间完全包含此时判断的区间[l,r] 
	if( lq<=l && r<=rq)
		return tree[p];
		
	//如果问题区间无法包含现在区间，比较问题区间与区间中点的关系，递归查询 
	int mid=(l+r)>>1;
	if(lq<=mid)
		ans+=RMQ_sum(lq,rq,l,mid,p<<1);
	if(rq>mid)
		ans+=RMQ_sum(lq,rq,mid+1,r,p<<1|1);
	return ans;
}

——区间问题2——
查询区间$[l,r]$中的最小/最大元素。

与上面的问题大同小异，修改一下回溯是更新条件即可。

//查询区间最大值或最小值 
int RMQ_min(int lq,int rq,int l,int r,int p)
//void RMQ_max(int lq,int rq,int l,int r,int p)
{

	int ans=0xffffff;
	//int ans=-0xffffff;
	
	//如果问题区间完全包含此时判断的区间[l,r] 
	if( lq<=l && r<=rq)
		return tree[p];
		
	//如果问题区间无法包含现在区间，比较问题区间与区间中点的关系，递归查询 
	int mid=(l+r)>>1;
	if(lq<=mid)
		ans=min(ans,RMQ_min(lq,rq,l,mid,p<<1));
		//ans=max(ans,RMQ_max(lq,rq,l,mid,p<<1));
	if(rq>mid)
		ans=min(ans,RMQ_min(lq,rq,mid+1,r,p<<1|1));
		//ans=max(ans,RMQ_max(lq,rq,mid+1,r,p<<1|1));
	return ans;
}

——线段树中元素值的修改——
假设此时要对$[l,r]$中的所有元素都加上一个$d$，也只要利用父节点，一步一步向下传导即可。

//朴素的更新方法_sum或min 
void update_sum(int lq,int rq,int l,int r,int p,int d)
//   update_min(int lq,int rq,int l,int r,int p,int d) 
{
	//当前区间超出查询范围，则不做修改 
	if(rq<l || lq>r)
		return;
		
	//精确的找到单个元素，进行修改 
	if(lq<=l&&r<=rq&&l==r)
	{
		tree[p]+=d;
		return;
	}
	
	//向下递归找到区间内元素，并更新 
	int mid=(l+r)>>1;
	update_sum(lq,rq,l,mid,p<<1,d);
	update_sum(lq,rq,mid+1,r,p<<1|1,d);
	
	//回溯更新父节点信息 
	pushup_sum(p);
	//pushup_min(p);
}

通过这段代码可以看出，每次修改元素的值，都需要精确地找到这个元素，找到一个元素并修改花费$O(logn)$的时间，修改区间又需要对所有元素查询并修改一遍，最终复杂度为$O(nlogn)$，这样的效率甚至还不如对数组进行简单的遍历操作，完全无法体现线段树的高效性。实际上，也没有必要精确找到所有元素，线段树的更新思想是区间整体修改的思想，对于一段连续的区间，只要在合适的深度进行整体操作即可。

线段树的精髓——O(logn)的区间修改操作

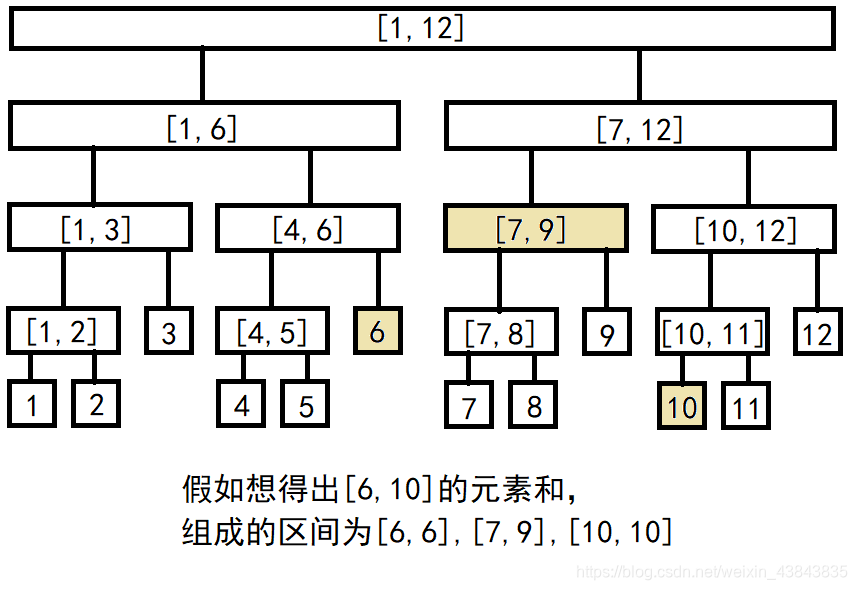
不妨参考之前区间求和的思路，假设要得出$[6,10]$的区间和，可以拆分为三个部分$[6,6]$、$[7,9]$、$[10,10]$，同样地，如果要对区间进行整体修改，也可以拆分成这三个部分。如果我们这时候维护的是区间最小值，父节点下的元素都加上$d$，等价于父节点也加上$d$，然后利用回溯，更新根节点；如果维护的是区间元素和，父节点点下元素加上$d$，等价于父节点加上$d\ast (r-l+1)$。这样的修改操作的复杂度约等于之前查询区间和或区间最小值的$O(logn)$（还会带一点常数）。

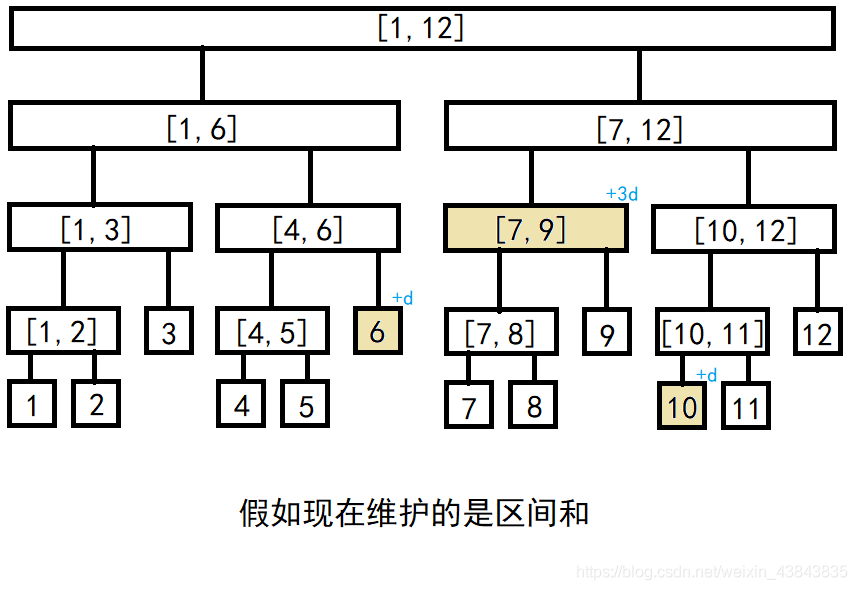
这样操作虽然快，同时却面临另一个问题，如果现在有两段交叉区间要进行修改，利用上面的不完全更新法，两区间重叠元素会出错。




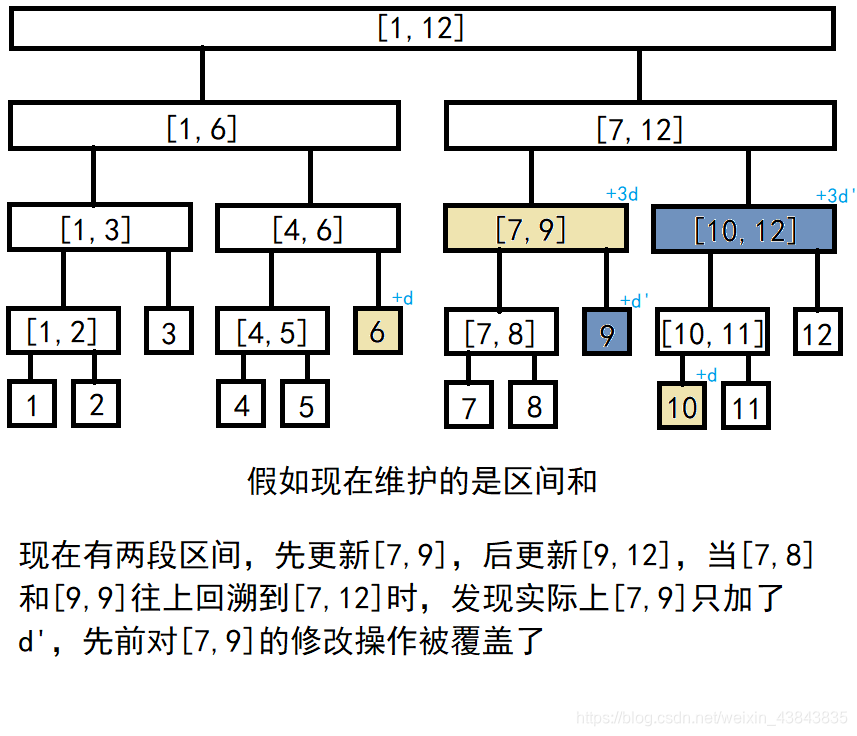
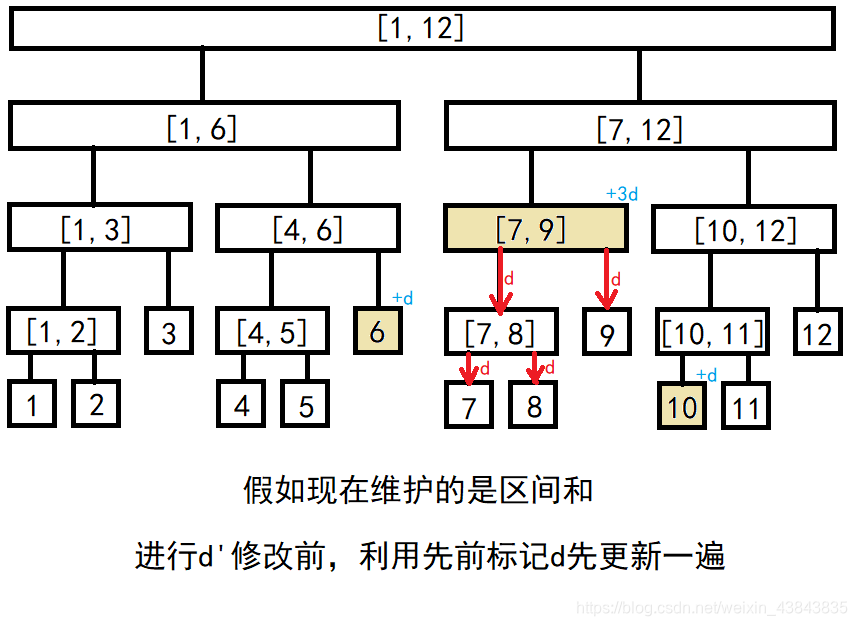
——lazytag——
线段树分块递归的好处就在于可以带着修改值$d$不断往树的底层走，在每次区间修改时，不妨留下一个值为$d$的标记，如果下一次这个区间需要往更深层挖掘，那就带着先前的标记$d$更新完它下面的全部元素，再用$d^{\prime }$更新本次需要的元素。为了实现这一想法，我们引入一个新数组$lazytag$，它的空间大小等于线段树的大小。

//区间整体修改
void rev(int p,int l,int r,int d)
{
	lazytag[p]+=d;
	tree[p]+=d*(r-l+1);
}
//向下传导lazytag
void pushdown(int p,int l,int r)
{
	int mid=(l+r)>>1;
	rev(p<<1,l,mid,lazytag[p]);
	rev(p<<1|1,mid+1,r,lazytag[p]);
	lazytag[p]=0;
	//注意此时父节点的标记已经被撤除，因为已经被传给两个儿子了 
} 
//更新
void update(int lq,int rq,int l,int r,int p,int d)
{
	if(lq>r || rq<l)
		return;
	if(lq<=l&&r<=rq)
	{
		tree[p]+=d*(r-l+1);
		lazytag[p]+=d;
		return;
	}
	
	pushdown(p,l,r);
	//先往下传导标记，再递归查找 
	 
	int mid=(l+r)>>1;
	update(lq,rq,l,mid,p<<1,d);
	update(lq,rq,mid+1,r,p<<1|1,d);
	
	pushup_sum(p);
	//标记传导完后，回溯就不会出错了 
} 

同时，为了使区间查询也不至于出错，同时也要加上向下传导标记的操作

//引入lazytag后，区间查询也需要作出一定修改
int RMQ_sum(int lq,int rq,int l,int r,int p)
{
	int ans=0;
	if(lq<=l&&r<=rq)
		return tree[p];
	int mid=(l+r)>>1;
	pushdown(p,l,r);
	if(lq<=mid)
		ans+=RMQ_sum(lq,rq,l,mid,p<<1);
	if(rq>mid) 
		ans+=RMQ_sum(lq,rq,mid+1,r,p<<1|1);
	return ans; 
} 

线段树模板（区间和）

以引言中的问题C为例

#include<iostream>
using namespace std;
int a[1000006];
int tree[4*1000006];
int lazytag[4*1000006];
int n,m;
inline void build_tree(int p,int l,int r)
{
	if(l==r)
	{
		tree[p]=a[l];
		return;
	}
	int mid=(l+r)>>1;
	build_tree(p<<1,l,mid);
	build_tree(p<<1|1,mid+1,r);
	tree[p]=tree[p<<1]+tree[p<<1|1];
}
inline void rev(int p,int l,int r,int d)
{
	lazytag[p]+=d;
	tree[p]+=d*(r-l+1);
}
inline void update(int lq,int rq,int l,int r,int p,int d)
{
	if(lq<=l&&r<=rq)
	{
		lazytag[p]+=d;
		tree[p]+=d*(r-l+1);
		return; 
	}
	int mid=(l+r)>>1;
	rev(p<<1,l,mid,lazytag[p]);
	rev(p<<1|1,mid+1,r,lazytag[p]);
	lazytag[p]=0;
	if(lq<=mid) update(lq,rq,l,mid,p<<1,d);
	if(rq>mid)  update(lq,rq,mid+1,r,p<<1|1,d);
	tree[p]=tree[p<<1]+tree[p<<1|1];
}
inline int RMQ_sum(int lq,int rq,int l,int r,int p)
{
	int ans=0;
	if(lq<=l&&r<=rq) return tree[p];
	int mid=(l+r)>>1;
	rev(p<<1,l,mid,lazytag[p]);
	rev(p<<1|1,mid+1,r,lazytag[p]);
	lazytag[p]=0;
	if(lq<=mid) ans+=RMQ_sum(lq,rq,l,mid,p<<1);
	if(rq>mid)  ans+=RMQ_sum(lq,rq,mid+1,r,p<<1|1);
	return ans;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;++i)
		cin>>a[i];
	build_tree(1,1,n);
	while(m--)
	{
		int num;
		cin>>num;
		if(num==1)
		{
			int lq,rq,d;
			cin>>lq>>rq>>d;
			update(lq,rq,1,n,1,d);
		}
		if(num==2)
		{
			int lq,rq;
			cin>>lq>>rq;
			cout<<RMQ_sum(lq,rq,1,n,1)<<endl;
		}
	}
	return 0;
}