【笔记】数据结构与算法 python-01-时间复杂度与空间复杂度

时间复杂度：

        用来估计算法运行时间的式子（单位），无法具体计算具体的时间，只能估算大概的时间复杂度。

         如何表示时间复杂度？

        通过O()表示，称为大O记法。

        O(1)

#################
print("Hello world?")
#################
a += b
#################
print("Hello world?")
print("Hello world?")
print("Hello world?")

        上述代码（用#隔开，是三段代码）的时间复杂度均为O(1)，可以理解为是一个基本单位，因为是一个量级的时间，通过一个O(1)估计。

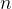        O()与O()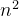

#######################
for i in range(n):
    print("Hello world?")
#######################
for i in range(n):
    for j in range(n):
        print("Hello world?")
#######################
for i in range(n):
    print("Hello world?")
    for j in range(n):
        print("Hello world?")

        上述代码中，第一段时间复杂度表示为O()，因为进行了n次循环，可以理解为这个量级远大于O(1)。当进行两次循环时，时间复杂度表示为O()，三层四层循环的话依次进行加权平方。注意：第三段代码的时间复杂度仍为O()，因为O(1)远小于O()，可以忽略。

        O()

while n >1:
    print('n')
    n = n // 2

        上述代码在运行过程中，数值会减半，因此不可等同于普通的循环时间复杂度。类比于对数函数，我们可以直观的看到，当n=64时，进行了6次循环。所以对于这种减半的情况，我们记时间复杂度为O()其中2可省略。

        如何简单快速判断算法的复杂度？

1. 确定问题的规模n；
2. 循环减半的过程；
3. 循环嵌套的层数；

        常见的时间复杂度排序

        对于后三个更加复杂的时间服再度问题，可以分解为前几种更优解，于是不在此讨论。

空间复杂度：

        用来估计算法内存占用大小的式子，通常我们会用空间换时间即尽可能的减少时间复杂度，提高运行速度。

        与时间复杂度的表示方法一样，也采用O()表示，

1. 常数空间复杂度，对于使用的变量个数可以记为： O(1) 
2. 线性空间复杂度，当使用了长度为n的一维列表时： O(n) 
3. 平方空间复杂度，当使用了m行n列的二维列表时： O(mn)
4. 对数空间复杂度，通常出现在递归算法中，随着输入规模呈对数增加： O(logn)
5. 线性对数空间复杂度，通常在一些高效的排序算法中，随着输入规模与对数乘积增加：O(nlogn)