【MATLAB学习笔记】数值方法——多维阻尼牛顿法（求极小值）

Infww

已于 2023-11-25 20:18:41 修改

阅读量1.3k

点赞数 18

分类专栏： MATLAB学习笔记文章标签： matlab 学习笔记算法

于 2023-11-25 20:12:07 首次发布

本文链接：https://blog.csdn.net/qq_53350487/article/details/134613762

版权

MATLAB学习笔记专栏收录该内容

13 篇文章 7 订阅

订阅专栏

前言

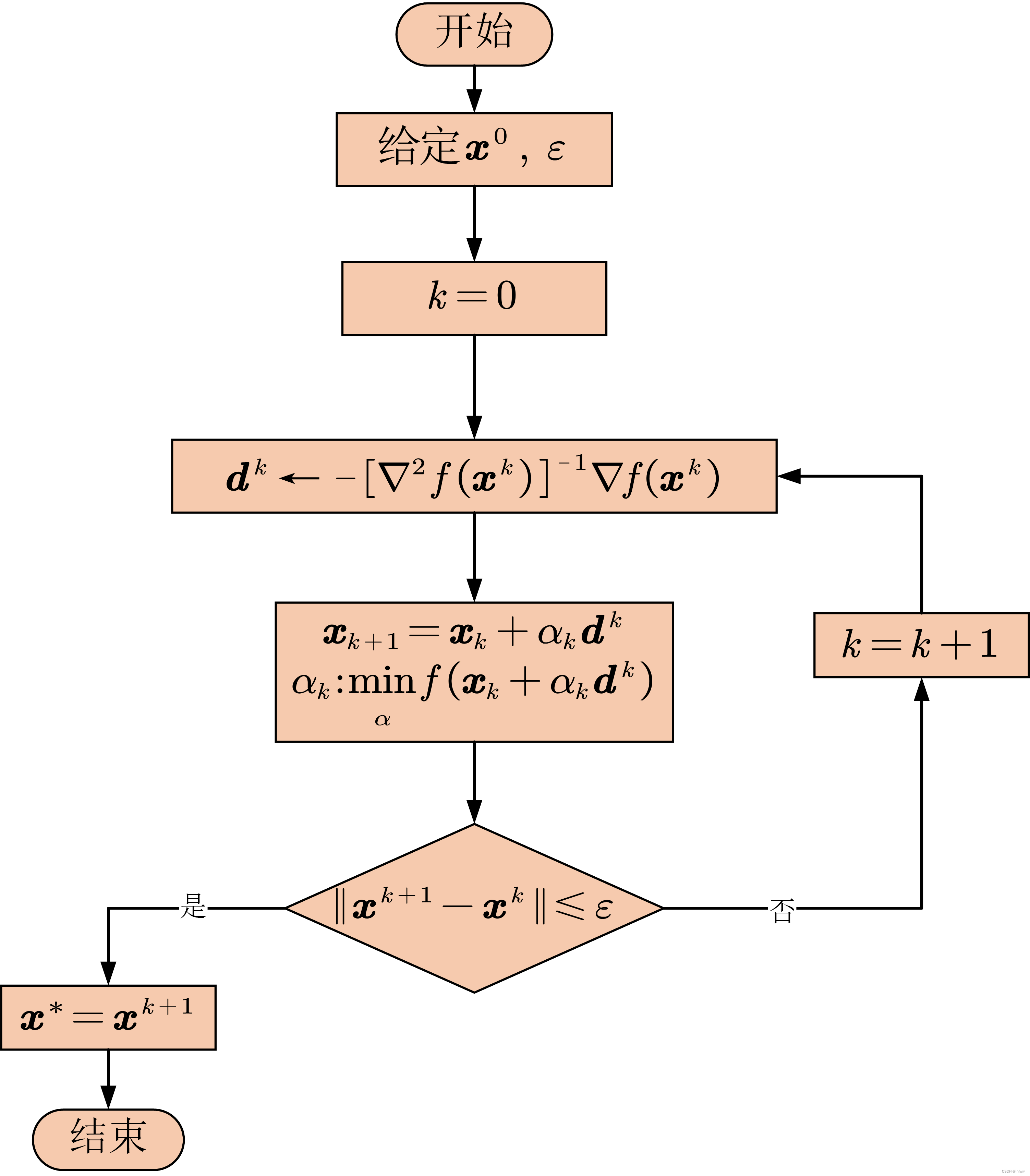
阻尼牛顿法（Damped Newton’s method）是一种求解非线性优化问题的数值方法，用于求解函数的极小值。其步骤如下：

具体步骤如下：

初始化：选择初始点 $\boldsymbol{x^0}$ ，以及允许误差 $\varepsilon$ 。
计算梯度：计算函数 $f(\boldsymbol x^k)$ 的梯度 $\nabla f(\boldsymbol x^k)$ 和Hessian矩阵 $H_f(\boldsymbol{x^0})$ 。
求解线性方程：解线性方程 $H_f(\boldsymbol{x^0})\boldsymbol d^k$ =- $\nabla f(\boldsymbol x^k)$ ，其中 $\boldsymbol d^k$ 是搜索方向。
更新参数：更新参数 $\boldsymbol{x}^{k+1}=\boldsymbol{x}^{k}+\alpha^k\boldsymbol d^k$ ，其中 $\alpha^k$ 为最优迭代步长，满足 $\underset{\alpha}{\min}f\left( \boldsymbol{x}^{k}+\alpha \boldsymbol{d}^k \right)$ 。
判断收敛：如果 $\left\| \boldsymbol{x}^{k+1}-\boldsymbol{x}^k \right\| \leqslant \varepsilon$ 则停止迭代，否则令 $k = k + 1$ ，返回步骤2。
结果输出：输出最优解 $\boldsymbol{x}^*=\boldsymbol{x}^{k+1}$ 。

算法流程图

在这里插入图片描述

算法代码

下面代码以二维为例：

function [x_min, f_min] = NewtonMethod_Damping(f,x0,eps,N)
    if nargin<2, x0 = [0,0]; end
    if nargin<3, eps=1e-4; end
    if nargin<4, N=100; end
    syms x1 x2 a
    f_fun = matlabFunction(f);

    k = 0;
    fprintf('阻尼牛顿法迭代开始(采用牛顿法进行一维搜索步长alpha):\n')
    fprintf('函数f(x) = %s迭代开始:\n',f)
    while true
        k = k  + 1;
        hs = hessian(f);    % 海塞矩阵
        hs_x0 = double(subs(hs,[x1,x2],x0));

        df = [diff(f,1,x1),diff(f,1,x2)];   % 梯度
        df_x0 = subs(df,[x1,x2],x0);
        dk = double(vpa(df_x0))/hs_x0;
        x = x0 - a * dk;
        
        % 求迭代步长
        fa = f_fun(x(1),x(2));
        a_value = Newton_minValue(fa);  % 使用一维牛顿法求解最优迭代步长
        x = subs(x,a,a_value);

        fprintf('k=%2.d, x_k=[%7.4f, %7.4f]^T, x_k+1=[%7.4f, %7.4f]^T, alpha=%7.4f\n',...
            k,x0(1),x0(2),x(1),x(2),a_value);

        if norm(abs(x -x0),2) < eps
            x_min = x;
            f_min = f_fun(x(1),x(2));

            fprintf(['已收敛!\nk=%2.d, x_k=[%7.4f, %7.4f]^T, x_min=x_k+1=[%7.4f, %7.4f]^T,' ...
                ' f_min=%8.4f\n'],k,x0(1),x0(2),x(1),x(2),f_min);
            break
        end

        if k > N
            x_min = x;
            f_min = f_fun(x(1),x(2));
            fprintf('超过最大迭代次数%N, 请调整容许误差或者最大迭代次数!\n',N)
            break
        end
        x0 = x;
    end

end

对于求解最优迭代步长，采用了一维牛顿法进行求解，具体可以看这篇文章。下面也给出一维牛顿法的程序代码：

function [x_star,f_star] = Newton_minValue(f_sym,x0,eps,N)
    % f_sym为所求函数, 符号函数
    % x0为初始点，默认为0
    % eps为允许误差, 默认为1e-4
    % N为最大迭代次数, 默认为500
    if nargin < 2, x0 = 0; end
    if nargin < 3, eps = 1e-4; end
    if nargin < 4, N = 1000; end

    f = matlabFunction(f_sym);
    df = matlabFunction(diff(f_sym));
    ddf = matlabFunction(diff(f_sym,2));
    
    k = 0;
%     fprintf('函数f=%s迭代开始:\n',f_sym)
    while true
        k = k + 1;

        x1 = x0 - df(x0)/(ddf(x0));
%         fprintf('k=%2.d, x0=%.4f, df=%9.4f, ddf=%9.4f, x1=%.4f\n',k,x0,df(x0),ddf(x0),x1)
        if norm(abs(x1-x0),'fro')<eps
%             fprintf('已收敛!结果如下：\nk=%2.d, x0=%.4f, x1=%.4f, f=%.4f',k,x0,x1,f(x1));
            x_star = x1;
            f_star = f(x_star);
            break
        end

        if k > N
            x_star = x1;
            f_star = f(x_star);
            fprintf('已经超出最大迭代次数%d!\n',N)
            break
        end
        x0 = x1;
    end

end

测试

测试函数如下：

syms x1 x2
f = (x1 - 2).^4 + (x1 - 2*x2).^2;

解析解

% 解析解
eqns = [diff(f,1,x1),diff(f,1,x2)];
[x1_min_true, x2_min_true] = solve(eqns,[x1,x2]);
x1_min_true = double(x1_min_true);
x2_min_true = double(x2_min_true);

x1_min_true	x2_min_true
2.0000	1.0000

算法解

eps = 1e-4;
x0 = [1,0];
[x_min_D, f_min_D] = NewtonMethod_Damping(f,x0,eps);

迭代过程如下：

阻尼牛顿法迭代开始(采用牛顿法进行一维搜索步长alpha):
函数f(x) = (x1 - 2*x2)^2 + (x1 - 2)^4迭代开始:
k= 1, x_k=[ 1.0000,  0.0000]^T, x_k+1=[ 1.3850,  0.7700]^T, alpha= 1.1551
k= 2, x_k=[ 1.3850,  0.7700]^T, x_k+1=[ 1.6921,  0.8074]^T, alpha= 1.4979
k= 3, x_k=[ 1.6921,  0.8074]^T, x_k+1=[ 1.8165,  0.9165]^T, alpha= 1.2127
k= 4, x_k=[ 1.8165,  0.9165]^T, x_k+1=[ 1.9030,  0.9481]^T, alpha= 1.4140
k= 5, x_k=[ 1.9030,  0.9481]^T, x_k+1=[ 1.9435,  0.9726]^T, alpha= 1.2524
k= 6, x_k=[ 1.9435,  0.9726]^T, x_k+1=[ 1.9693,  0.9843]^T, alpha= 1.3701
k= 7, x_k=[ 1.9693,  0.9843]^T, x_k+1=[ 1.9824,  0.9913]^T, alpha= 1.2778
k= 8, x_k=[ 1.9824,  0.9913]^T, x_k+1=[ 1.9903,  0.9951]^T, alpha= 1.3462
k= 9, x_k=[ 1.9903,  0.9951]^T, x_k+1=[ 1.9945,  0.9972]^T, alpha= 1.2932
k=10, x_k=[ 1.9945,  0.9972]^T, x_k+1=[ 1.9969,  0.9985]^T, alpha= 1.3329
k=11, x_k=[ 1.9969,  0.9985]^T, x_k+1=[ 1.9983,  0.9991]^T, alpha= 1.3024
k=12, x_k=[ 1.9983,  0.9991]^T, x_k+1=[ 1.9990,  0.9995]^T, alpha= 1.3254
k=13, x_k=[ 1.9990,  0.9995]^T, x_k+1=[ 1.9995,  0.9997]^T, alpha= 1.3078
k=14, x_k=[ 1.9995,  0.9997]^T, x_k+1=[ 1.9997,  0.9998]^T, alpha= 1.3211
k=15, x_k=[ 1.9997,  0.9998]^T, x_k+1=[ 1.9998,  0.9999]^T, alpha= 1.3110
k=16, x_k=[ 1.9998,  0.9999]^T, x_k+1=[ 1.9999,  1.0000]^T, alpha= 1.3187
已收敛!
k=16, x_k=[ 1.9998,  0.9999]^T, x_min=x_k+1=[ 1.9999,  1.0000]^T, f_min=  0.0000

总代码

clc;clear;close all
%% 
syms x1 x2
f = (x1 - 2).^4 + (x1 - 2*x2).^2;
eqns = [diff(f,1,x1),diff(f,1,x2)];
[x1_min_true, x2_min_true] = solve(eqns,[x1,x2]);
x1_min_true = double(x1_min_true);
x2_min_true = double(x2_min_true);

eps = 1e-4;
x0 = [1,0];
[x_min_D, f_min_D] = NewtonMethod_Damping(f,x0,eps);

function [x_min, f_min] = NewtonMethod_Damping(f,x0,eps,N)
    if nargin<2, x0 = [0,0]; end
    if nargin<3, eps=1e-4; end
    if nargin<4, N=100; end
    syms x1 x2 a
    f_fun = matlabFunction(f);

    k = 0;
    fprintf('阻尼牛顿法迭代开始(采用牛顿法进行一维搜索步长alpha):\n')
    fprintf('函数f(x) = %s迭代开始:\n',f)
    while true
        k = k  + 1;
        hs = hessian(f);    % 海塞矩阵
        hs_x0 = double(subs(hs,[x1,x2],x0));

        df = [diff(f,1,x1),diff(f,1,x2)];   % 梯度
        df_x0 = subs(df,[x1,x2],x0);
        dk = double(vpa(df_x0))/hs_x0;
        x = x0 - a * dk;
        
        % 求迭代步长
        fa = f_fun(x(1),x(2));
        a_value = Newton_minValue(fa);  % 使用一维牛顿法求解最优迭代步长
        x = subs(x,a,a_value);

        fprintf('k=%2.d, x_k=[%7.4f, %7.4f]^T, x_k+1=[%7.4f, %7.4f]^T, alpha=%7.4f\n',...
            k,x0(1),x0(2),x(1),x(2),a_value);

        if norm(abs(x -x0),2) < eps
            x_min = x;
            f_min = f_fun(x(1),x(2));

            fprintf(['已收敛!\nk=%2.d, x_k=[%7.4f, %7.4f]^T, x_min=x_k+1=[%7.4f, %7.4f]^T,' ...
                ' f_min=%8.4f\n'],k,x0(1),x0(2),x(1),x(2),f_min);
            break
        end

        if k > N
            x_min = x;
            f_min = f_fun(x(1),x(2));
            fprintf('超过最大迭代次数%N, 请调整容许误差或者最大迭代次数!\n',N)
            break
        end
        x0 = x;
    end

end

function [x_star,f_star] = Newton_minValue(f_sym,x0,eps,N)
    % f_sym为所求函数, 符号函数
    % x0为初始点，默认为0
    % eps为允许误差, 默认为1e-4
    % N为最大迭代次数, 默认为500
    if nargin < 2, x0 = 0; end
    if nargin < 3, eps = 1e-4; end
    if nargin < 4, N = 1000; end

    f = matlabFunction(f_sym);
    df = matlabFunction(diff(f_sym));
    ddf = matlabFunction(diff(f_sym,2));
    
    k = 0;
%     fprintf('函数f=%s迭代开始:\n',f_sym)
    while true
        k = k + 1;

        x1 = x0 - df(x0)/(ddf(x0));
%         fprintf('k=%2.d, x0=%.4f, df=%9.4f, ddf=%9.4f, x1=%.4f\n',k,x0,df(x0),ddf(x0),x1)
        if norm(abs(x1-x0),'fro')<eps
%             fprintf('已收敛!结果如下：\nk=%2.d, x0=%.4f, x1=%.4f, f=%.4f',k,x0,x1,f(x1));
            x_star = x1;
            f_star = f(x_star);
            break
        end

        if k > N
            x_star = x1;
            f_star = f(x_star);
            fprintf('已经超出最大迭代次数%d!\n',N)
            break
        end
        x0 = x1;
    end

end