边缘提取（三维重建知识）

1、边缘提取的作用是什么

上图当中有一个用线条组成的图像，通过这些线条我们就可以很好的理解这张图像，但是现实生活中很多图像都不是线条组成的，还有其他很多因素，那么仅仅通过线条就能理解图像的话，就可以把线条提取出来，帮助我们理解图像，这就是进行边缘提取的目的。所谓的边缘就是与周围点相差比较大的点，或者叫做不连续的点，或者叫做图像信号突变的点。

2、边的类型

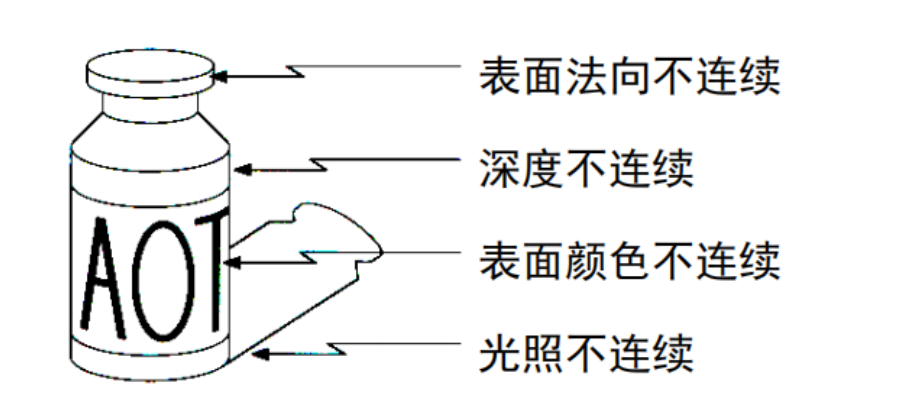
可以看到上图一共有四种常见边的类型。第一种边是面相交形成（面不连续）的边。第二种是深度信息不连续而造成的边，例如瓶子在像平面成像的时候就会造成深度信息不连续的边，也就是瓶子的边缘。第三种是瓶子上的一些信息，如字母造成的边。第四种是影子（光线不连续）造成的边。那么为什么要区分边的类型，因为执行不同任务时需要掌握不同的边缘信息。例如机器人抓东西，就需要知道这个东西的面相交的边和深度信息不连续的边。如果是要识别语义信息，就需要知道字母造成的边。还有如果要知道物体的位置，就要识别影子造成的边。

3、边缘如何提取

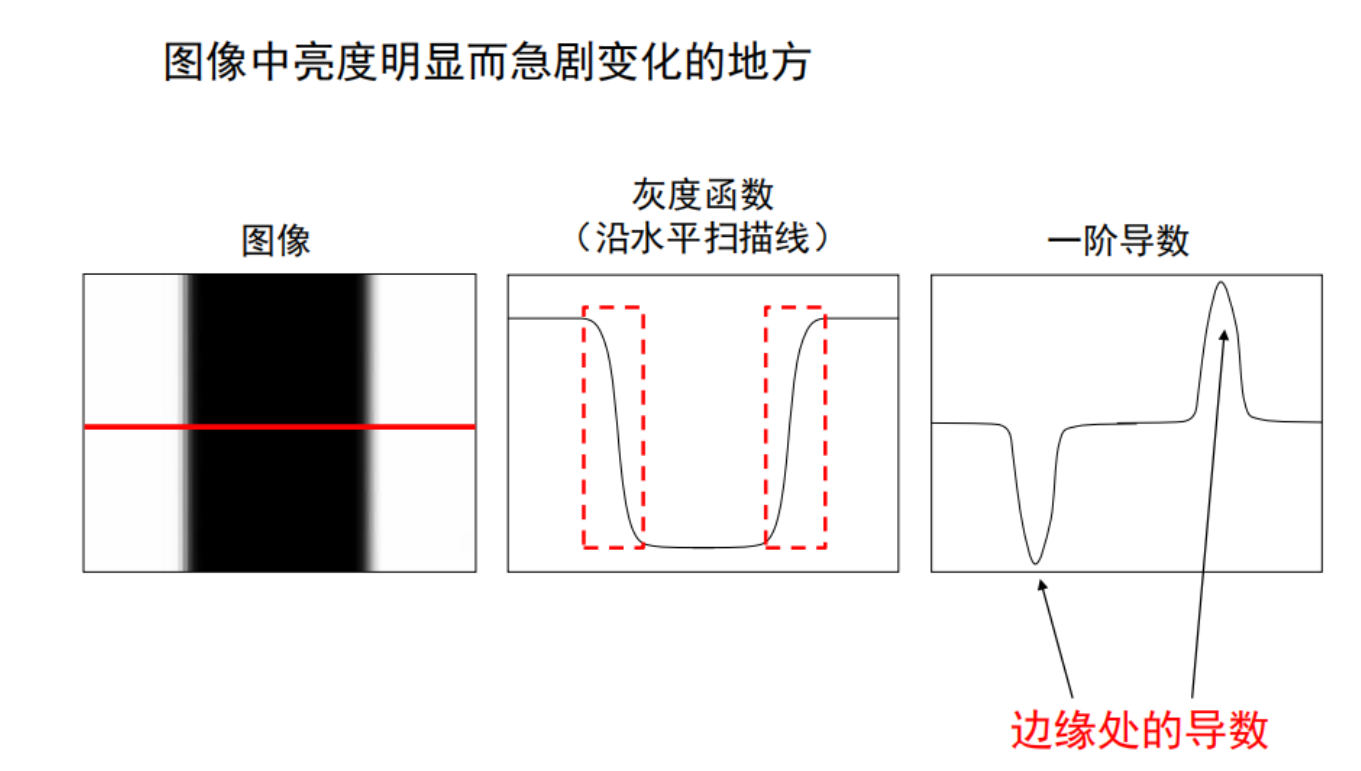
根据上图可以看到两条边是黑白分离的那里，红色的线是指图像上这一行上的信号变化，右边是它信号变化的图，可以看出是先白后黑，突然变化的两点就是边缘线上面的点，如何求这两点，是对对应的函数进行求导然后取极值点，极值点就是这个突然变化的点。

那么上面所说的导数求极限中的导数如何求。上图的第一行是f（x，y）对于x求导数的一个定义，但是这里对于求极限不太友好，干脆定为1。近似符号

直接不要了。可以看到第二行实际上就是我图像上右边的一个点f（x+1，y）减去我自己f（x，y），这被定义为图像里面的求导方式。那么这就可以利用卷积来做，即定义一个卷积核

套在对应的点上就是这样一个效果。

那么得出一个结论，卷积还可以用来求导数。

上图中哪张图是利用对x求导卷积核进行卷积后的图像。

上图已经给出了答案，左边是对x求导卷积的效果，左边是对y求导卷积的效果。因为对x求导，就会使图片横向差异很大的地方进行保留，对y求导，就会使图片竖向差异很大的地方进行保留。

上述通过函数导数推导的图像导数得到的卷积

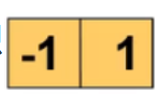
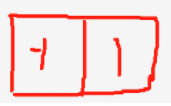
，是我们自己定义的，那么基于这个图像导数得到的卷积还有很多种。如上图，第一个Prewitt，它也是根据图像导数得到边缘提取卷积，它的意义在于，不对本身要验证是不是边缘点的点进行处理，而是对旁边两侧的点进行处理，也就是右边一侧的值减去左边一侧的值，如果差异很大的话，就说明位于中间的点极可能是一个边缘点。第二个是Sober，它可以分解为两个向量相乘（1，2，1）（-1，0，1）T，其中前一个是高斯卷积，后面是边缘提取卷积，也就是Sober在进行边缘提取的时候，要先利用高斯滤波进行一个平滑处理之后，在进行边缘提取，因此Sober对于噪声点没有那么敏感。最后是Roberts，它是验证位于斜线（斜对角）上的点是不是边缘点，如Mx验证的就是

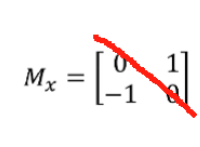
135°的斜线上的点，考察这条斜线两侧的点的值差异大不大；My验证的就是

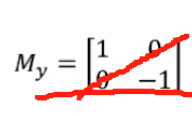
45°的斜线上的点，考察这条斜线两侧的点的值差异大不大。值得注意的是测试模板（边缘卷积）考虑的方向一定是与边缘线垂直的方向。

4、梯度

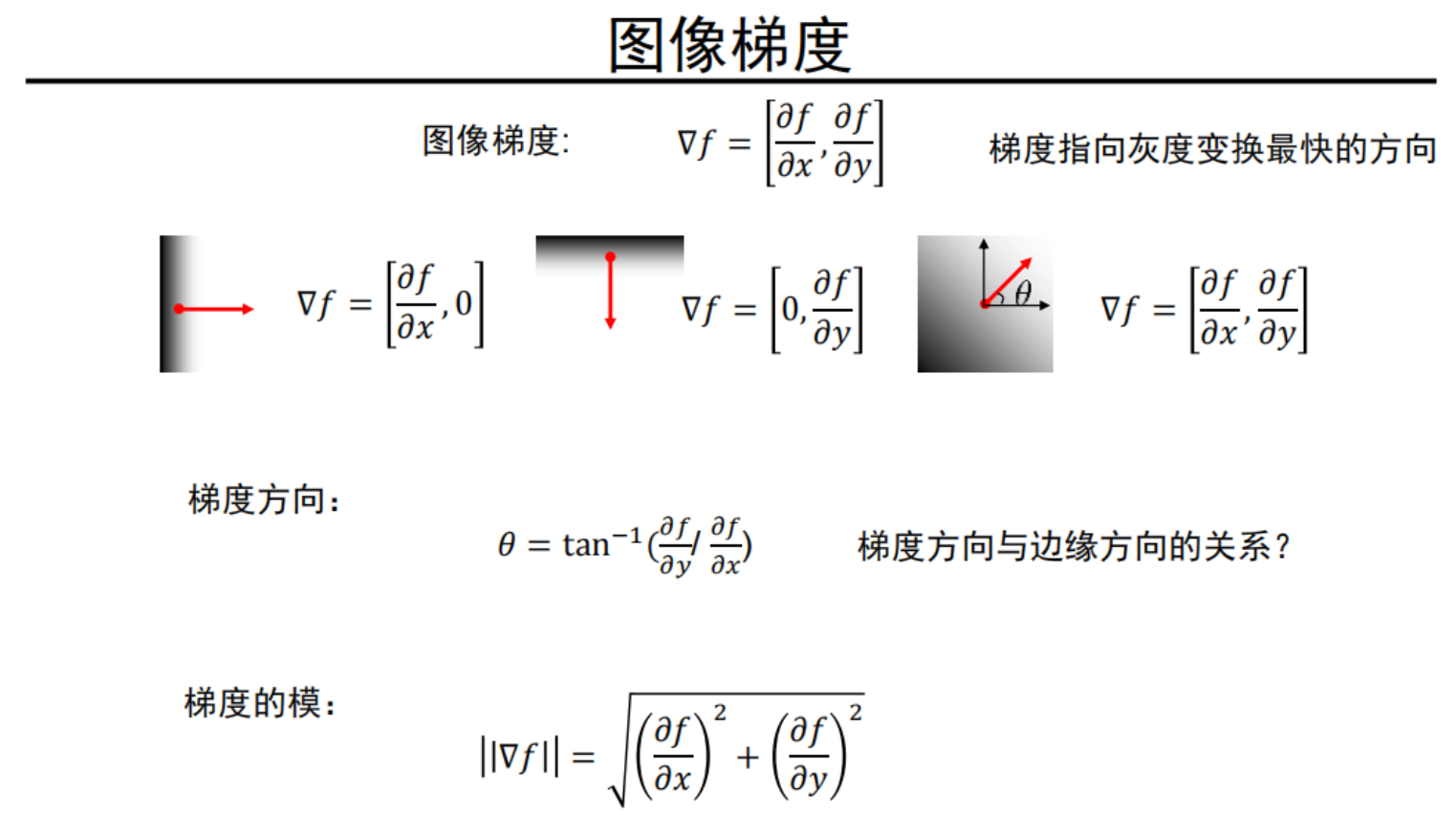
图片的梯度是指对图片上的一个点的x、y方向分别求导，求导结果组成的向量就是梯度值

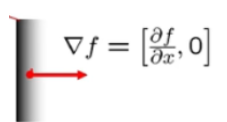
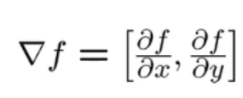的梯度值中x方向有值，而y方向没得，其原因是y方向没有边缘点。

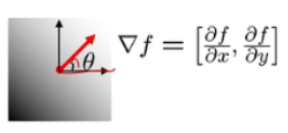
的梯度值，x、y方向都有值，因为x、y方向都有边缘点，梯度方向与x方向的夹角θ的值为

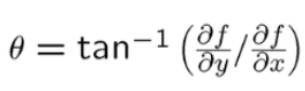
。值得注意的是梯度的方向是指这个点周围信号变化最大的方向，另外梯度方向和边是垂直的关系。最后还有一个公式

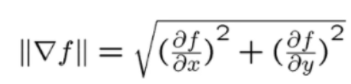
叫做梯度幅值，它的值越大表明这个点是边缘点的可能性越大。

上图分别表示的是原图、x方向求导卷积的效果、y方向求导卷积的效果、幅值图。最后一张图幅值图就是我们一个提取轮廓比较清晰的图了，它是前两个图平方求和取根号的结果，即

。

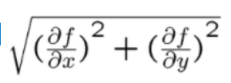5、噪声对于边缘提取的影响

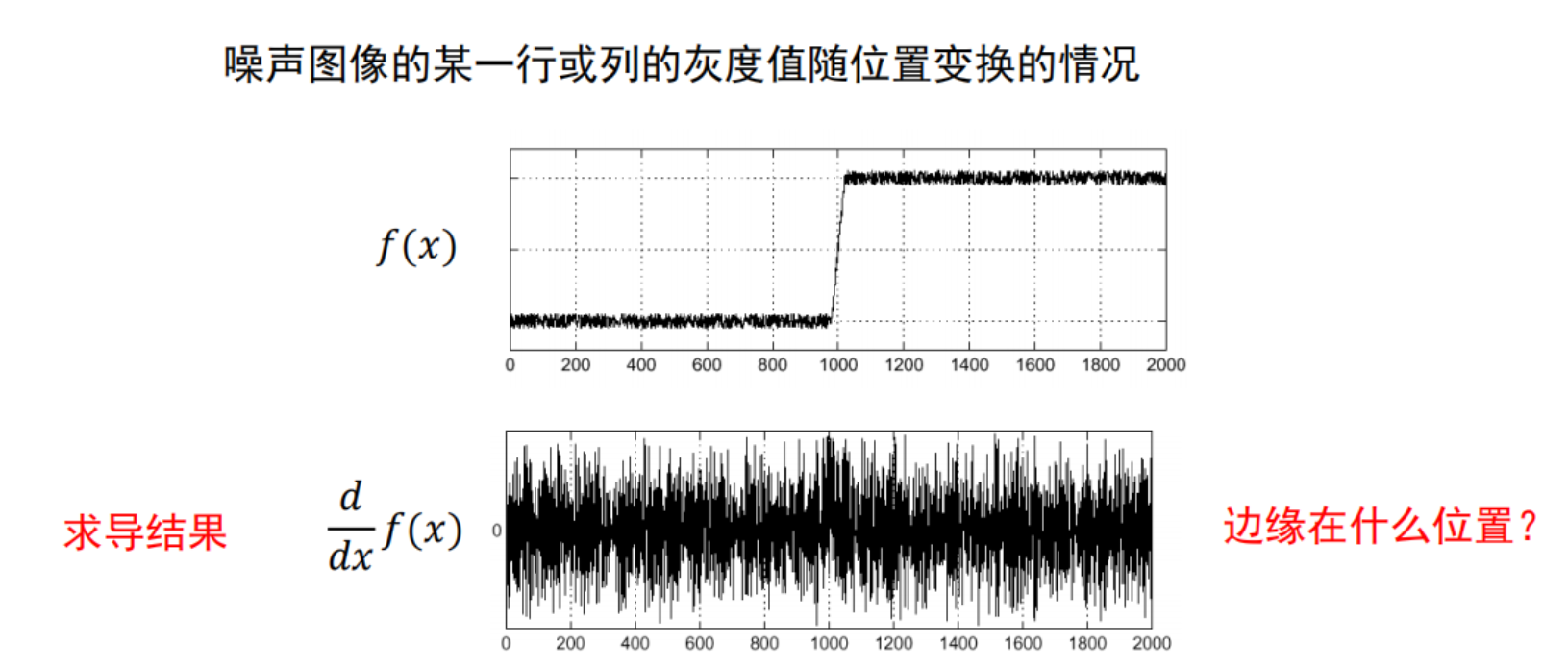
使用刚刚提及的边缘提取器（Prewitt、Roberts、Sober）对现实中的图片进行边缘提取。现实中图片的信号如上图，可以很明显的看出哪里是边缘，但同时现实中的图像中有很多的噪声点，信号并不是一条光滑的线，因此如果直接用边缘提取器对其进行求导，可以看到结果如上图，从这个梯度中是很难找到极大值和极小值，也就是边缘点非常难提取。

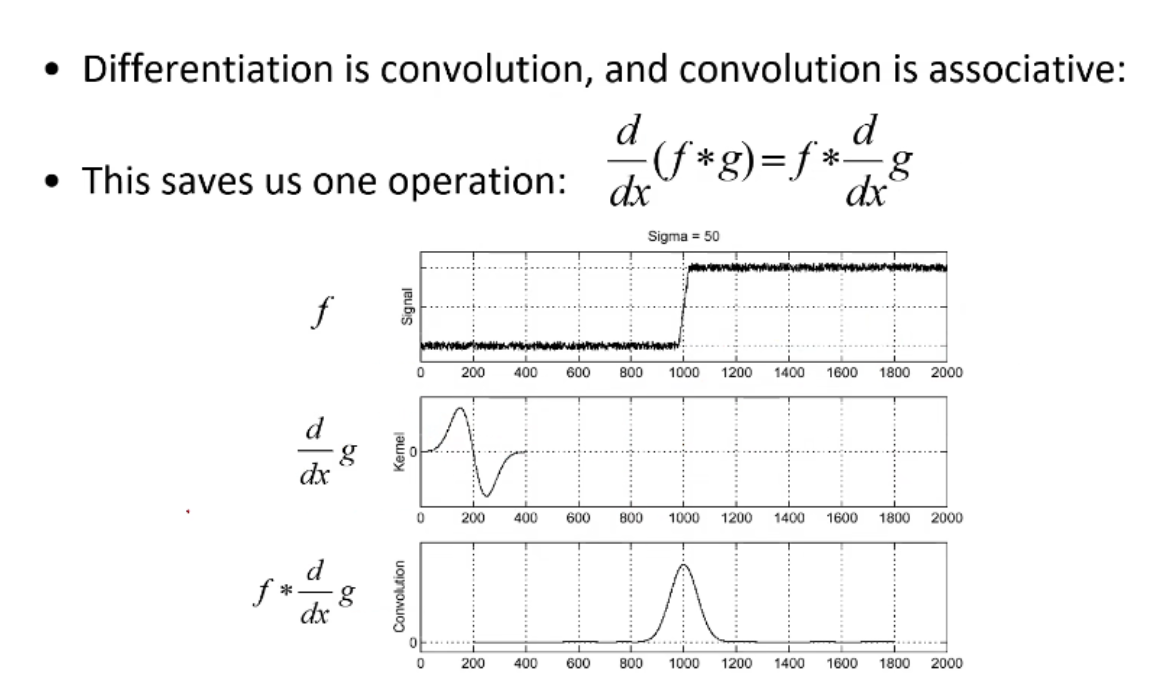
针对于现实图像有很多噪声点的问题，首先要对图像进行处理，也就是先用一个平滑滤波器（高斯、中值）进行滤波，如上图就是采用了一个高斯滤波器进行滤波，滤波后的结果看得出来明显减少了很多的噪声点，信号变得很光滑，在对此结果进行边缘提取卷积的求导操作，可以看到极值点（边缘点）很明显。所以在对真实图像进行边缘提取的时候最好是先进行平滑，在进行边缘提取，这样带来的代价就是非常耗时，因为连续进行了两次卷积，而卷积是很费时的。

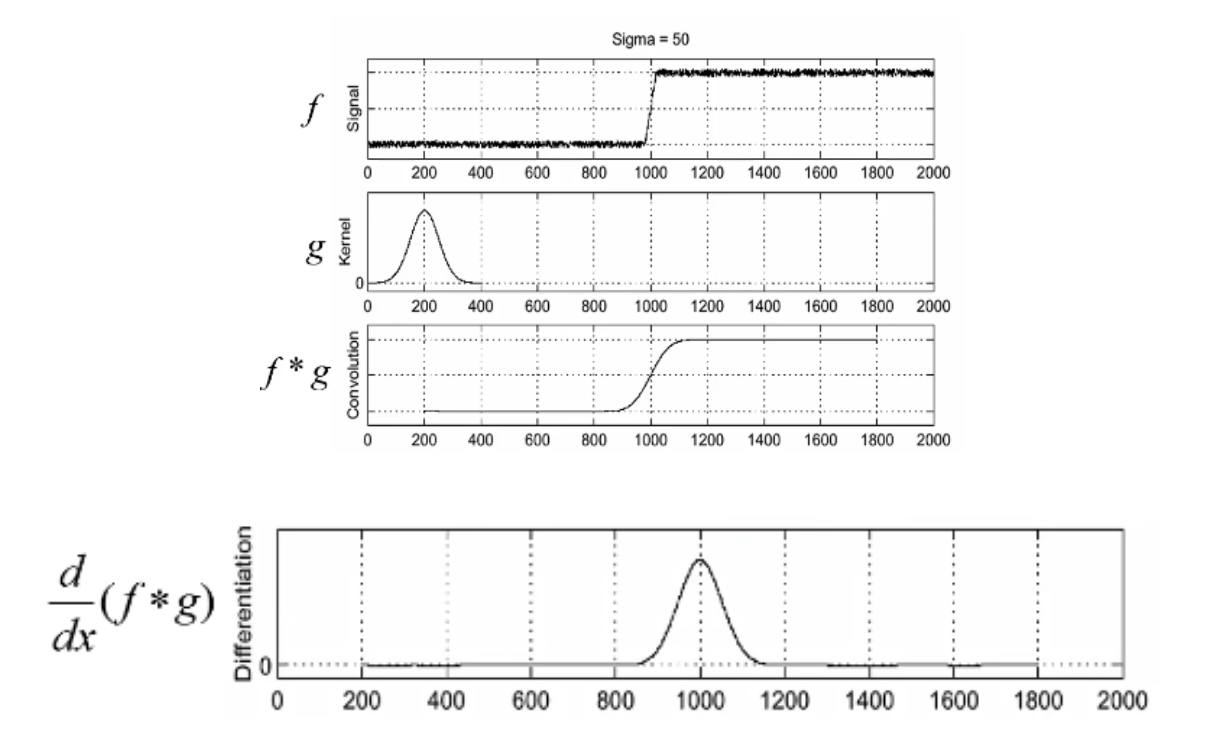
那么针对于上述的时间问题，可不可以把高斯卷积和边缘卷积结合一下，最终只让图片卷积一次，这样就比较节约时间了。上图可以看到

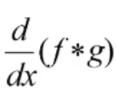
，其中f*g表示先将图片进行高斯滤波，然后再用d/dx求导进行边缘卷积。那么卷积有交换律，就可以将上述式子转换为

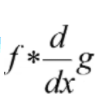
，先算*后面一部分（卷积的结合律），也就是对于高斯卷积进行求导，这个式子

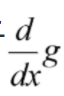
也叫做高斯卷积的一阶导或者是高斯卷积偏导，然后在将图片利用高斯一阶导的模板进行卷积，图片只卷积一次这样会快很多，因为

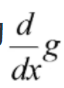
很小，g高斯卷积就是一个模板，对他求导很快就可以完成。

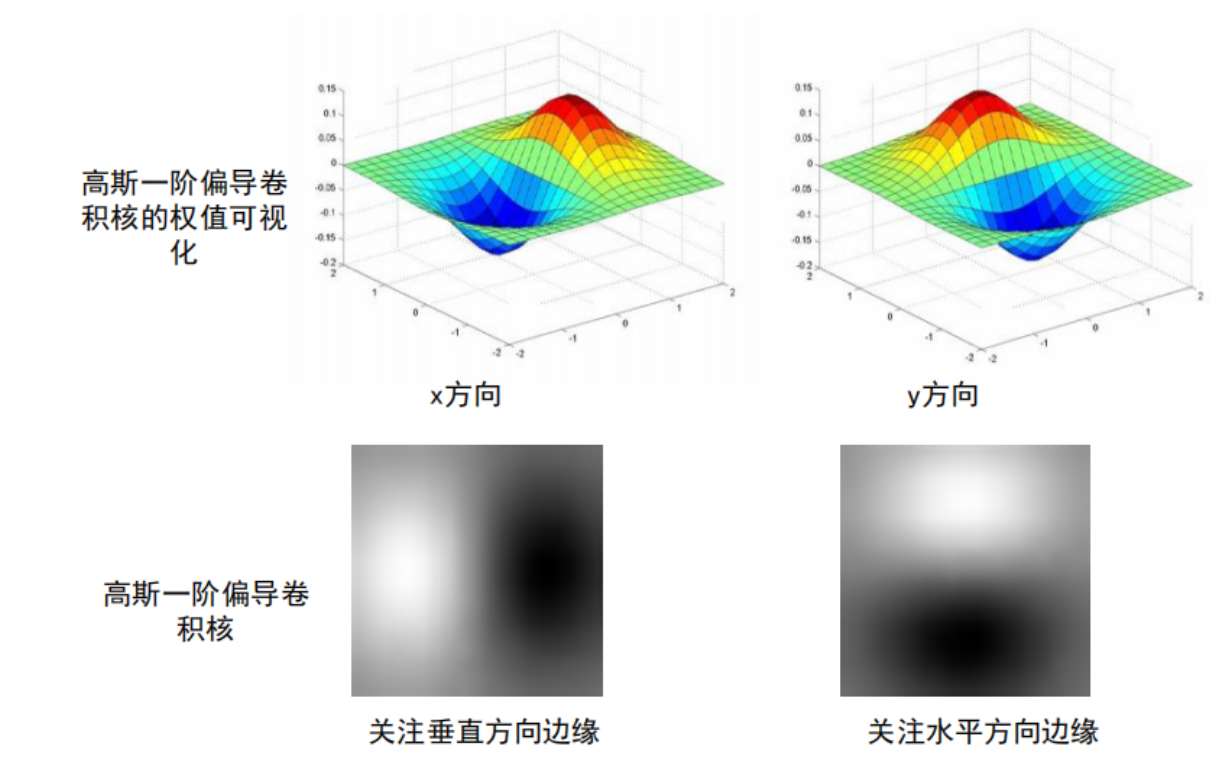
上图是高斯卷积一阶导的三维表示，左边是高斯卷积对于x方向的偏导，右边是高斯卷积对于y方向的偏导。那么对于这个偏导数来说，它是不可分离的（分离意思是能够分开为两个独立的乘法），因为求偏导后的式子，会加上一个x或者y变量。上图中的下边部分是高斯卷积一阶导的二维表示，越白的地方，权重值越高，越黑的的方，权重值越低（负值）。右图对应的是对x求偏导（竖状纹理增强），右图对应的是对y求偏导（横状纹理增强）。

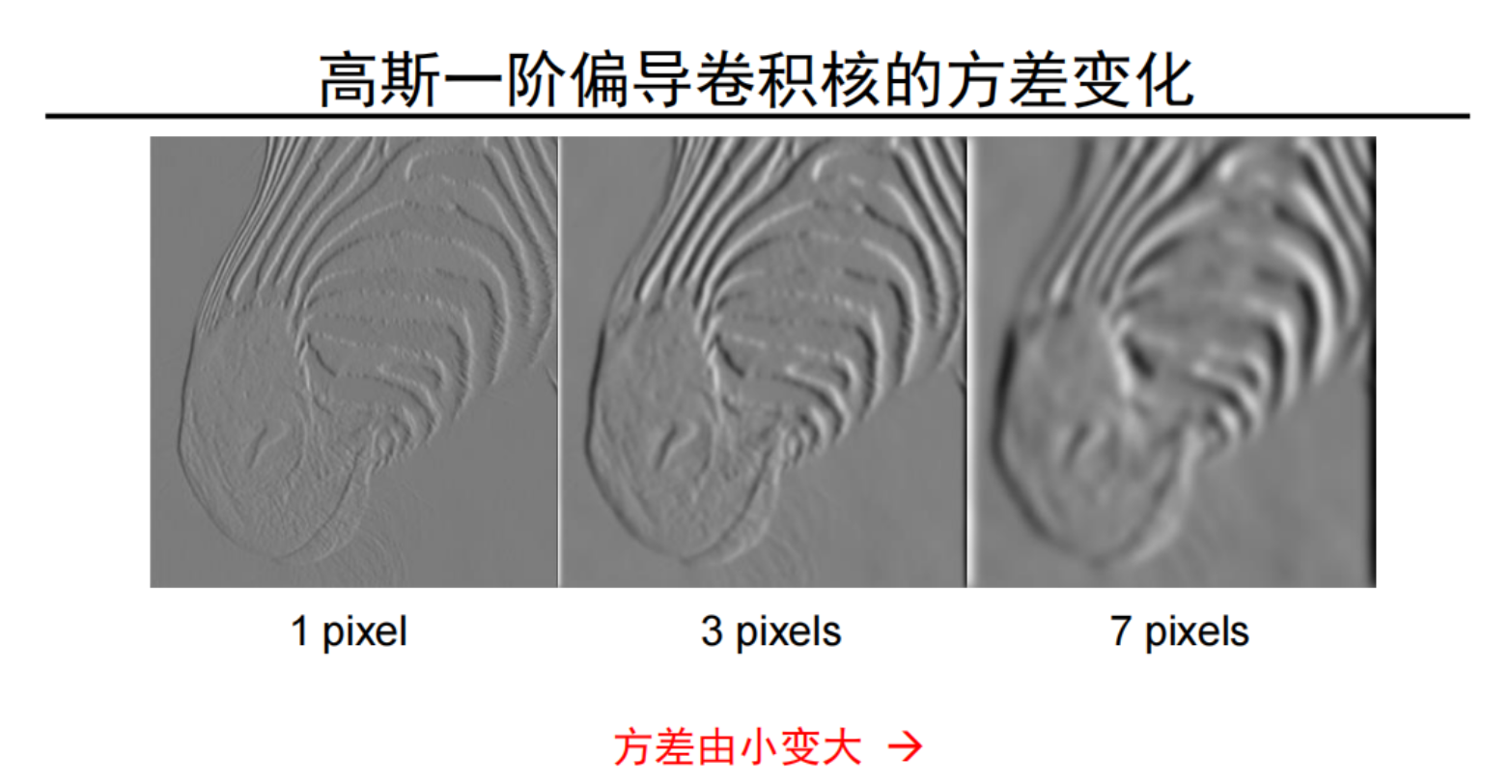
将高斯卷积一阶导应用在一张图像上，之后就可以得到这张图象去噪后的边提取结果。上面是设置高斯卷积一阶导不同的方差值的效果，可以看到方差值越大，提取的边缘信息越模糊。在高斯卷积公式中有两个参数：窗宽和方差值，那么高斯卷积一阶导也有这两个参数，从上节课中了解到这两个参数只要知道了其中一个就可以推算出另一个（一般如果给定了，那么卷积核的大小就是（3+1）x（3+1）），因此这里只改变了高斯卷积一阶导的一个参数。这个可以按照任务的需要进行调整 ，比如我们做的人脸识别任务，这个值就可以调小一点，因为鼻子眼睛嘴巴这些细节的特征是需要识别出来的，但是如果是目标检测任务，我们只需要物体的一个轮廓，太多的细节反而对我们的结果造成影响，这时候就将值就可以调大一点。

6、高斯（平滑）滤波器与高斯一阶导滤波器的对比

首先看到高斯（平滑）滤波器。第一它的目的是去除图片的高频信号，也就是去噪。第二它没有负值（从卷积部分高斯（平滑）滤波器的图像可知）。第三它的加权求和的值为1（从卷积部分它的计算过程可知）。其次是高斯一阶导滤波器。第一它的目的是提取图像的边缘信息。第二它有负值（从高斯一阶导滤波器的图像可以看出）。第三它的加权求和的值为0，如果加权求和不为0，将高斯一阶导滤波器作用在一张白纸上面的时候，那么这张白纸也会有边。第四它的值越大，表明这个点越可能是边缘点，也可能是噪声点（虽然高斯一阶导滤波器具有去噪的功能，但是也不排除是噪声点的可能性）。

7、Canny算法（Canny边缘提取器）

7.1 幅值临界值

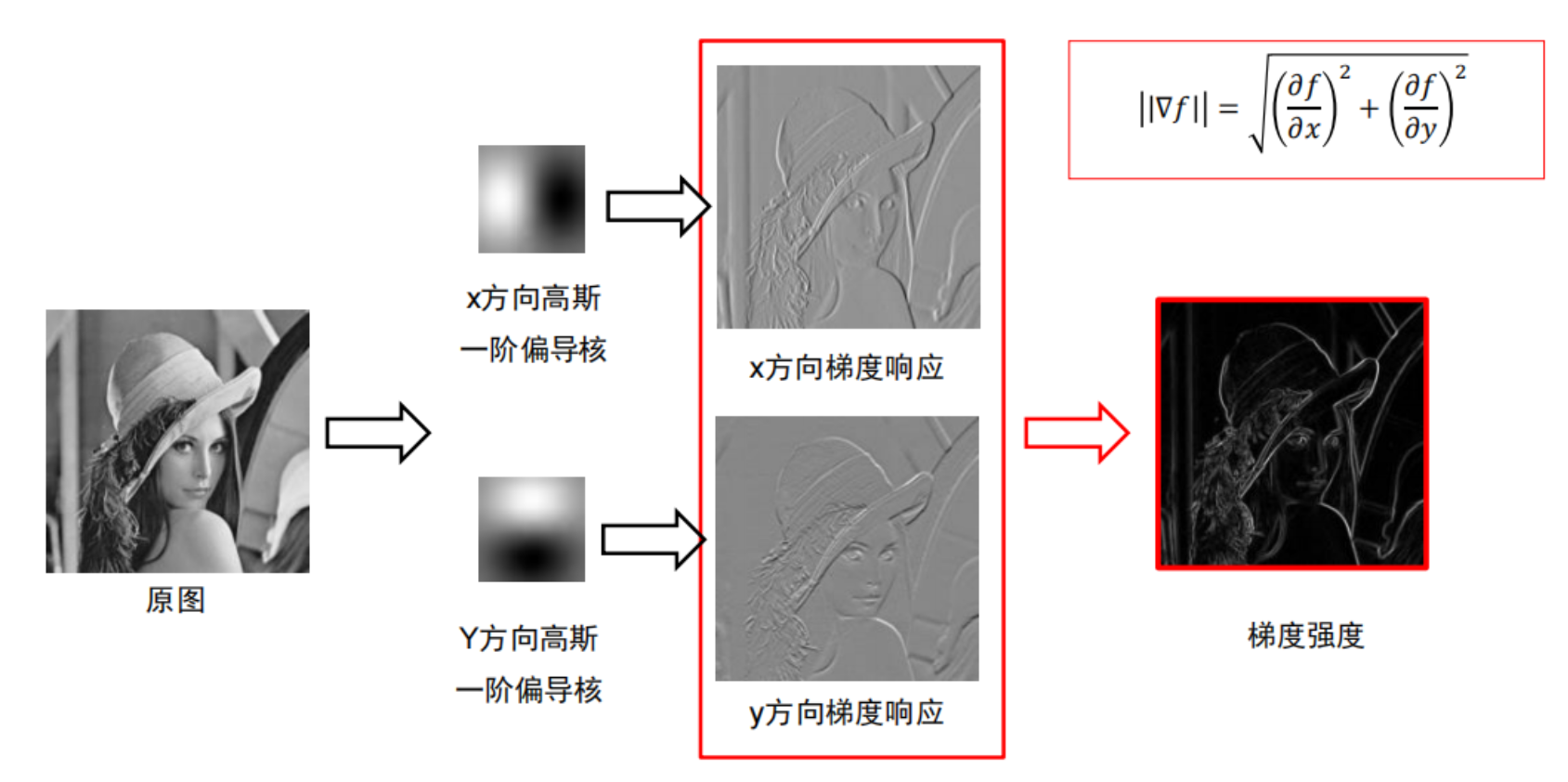
Canny算法的提出到今天已经几十年了，但是仍然是最为经典的边缘提取算法。接下来将对其做介绍。首先看到上面的第一张图，使用高斯一阶导滤波器对于原始图像进行x和y方向的滤波，然后利用公式

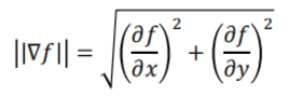
，求取图像的幅值（其中的偏导不是对图像信号求偏导，而是高斯一阶导

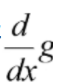
得到图像的一个大概轮廓。

我们知道幅值越大，那么这个点就越可能是边缘点，那么幅值也需要一个临界值，比如低于30的幅值就不被认为是边缘点（可能为噪声点），因此可以定义一个幅值的临界值，对图像进行第二次去噪（第一次是利用高斯一阶导滤波器进行求偏导），上图就是进行第二次去噪的效果图。

7.2 非极大值抑制

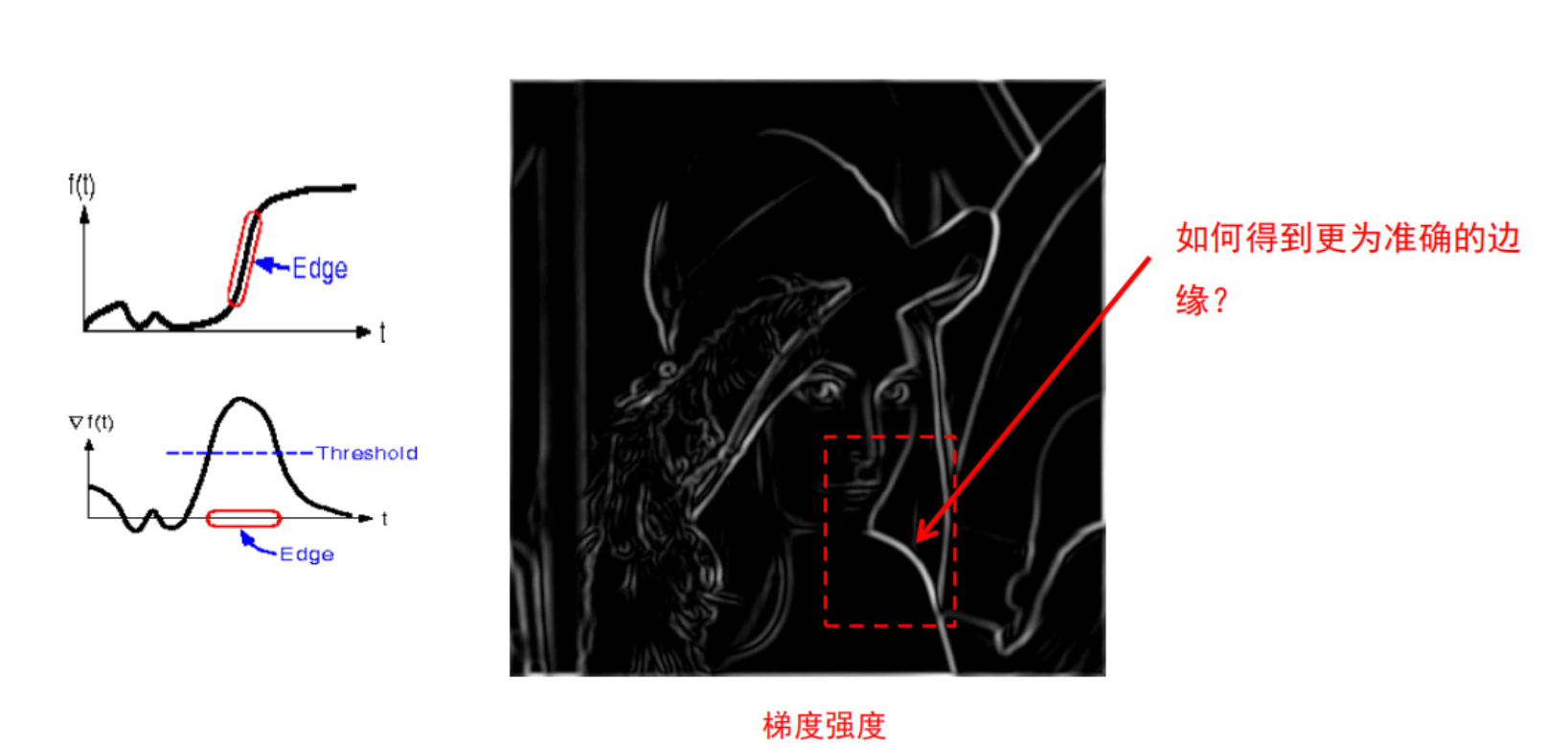
但是从最终边缘提取的效果图中可以看出红框部分的线条特别粗，但是我们真正需要提取的边缘是希望比较细的。造成这样的原因可以看到左图，第一个是图像信号的变化曲线，可以看到边缘部分是缓慢上升的。第二个图是图像信号的幅值图，定义一个临界值，也就是蓝色虚线，可以看出在虚线上面的一部分都被认为是边缘部分，它对应的横坐标t值比较大，因此会造成最后提取的边缘线条比较粗。造成这样的原因就是因为图像的边缘信号都是缓慢上升的，而不是垂直上升，就算是垂直上升，被高斯一阶导滤波器平滑后，也会变成缓慢上升。

为了解决边缘信号缓慢上升造成的提取的边缘线条过粗的缺点，提出了非极大值抑制的方法。看到上图也就是取边缘粗线条上每个边缘点的梯度方向（与边缘线垂直的方向），找到距离该边缘点的一个像素的两个邻居，比较这三个点的幅值值，看我们取的这个边缘点的幅值是不是最大，如果是最大，那么我就是真正的边缘点，其他两个邻居就没有存在的必要了；如果不是最大，说明我们取的这个点就不是真正的边缘点，就把这个点去掉。但是我们取一个点的两个邻居点的时候，是取的梯度方向距离一个像素的两个点，这两个邻居点就有可能没在正好的像素点上，这时候就需要找它相邻的四个点，对四个点的幅值进行加权求和得到邻居点的幅值，进而在进行非极大值抑制的操作。上图的最右边就是经过非极大值抑制后的效果可以看出线条明显细了很多。

7.3 双门限（双阈值）方法

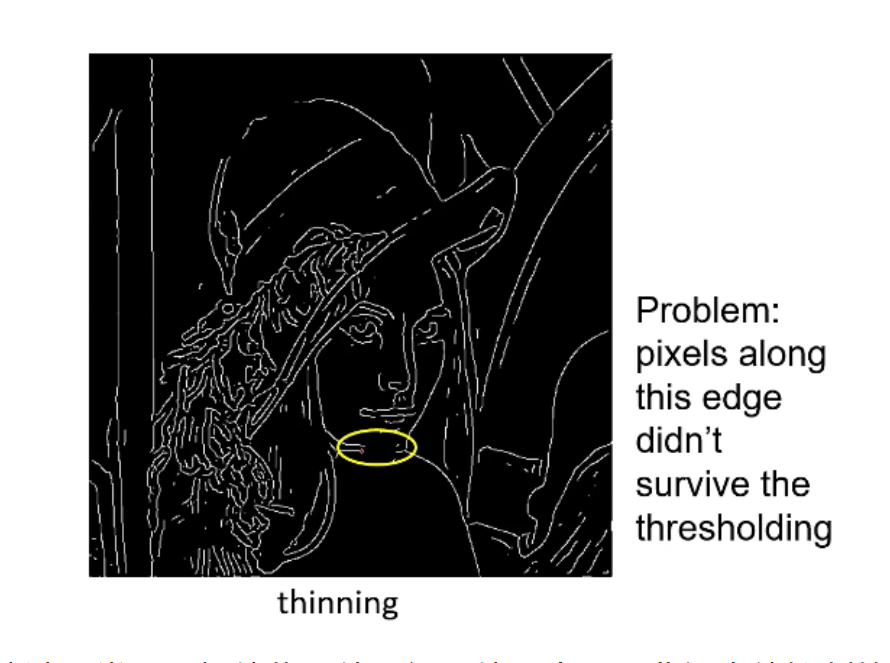
上图是经过了高斯一阶导滤波器卷积、幅值临界值（门限值）去噪和非极大值抑制的最终效果。可以最终效果还是有问题，也就是这张图象中黄框里的线条没有了。这就是因为在设置幅值门限值的时候，门限值设置得过高，导致一些边缘线条也被舍去。

上图就是门限值设置过低，导致最终的效果图多了很多的噪声边。

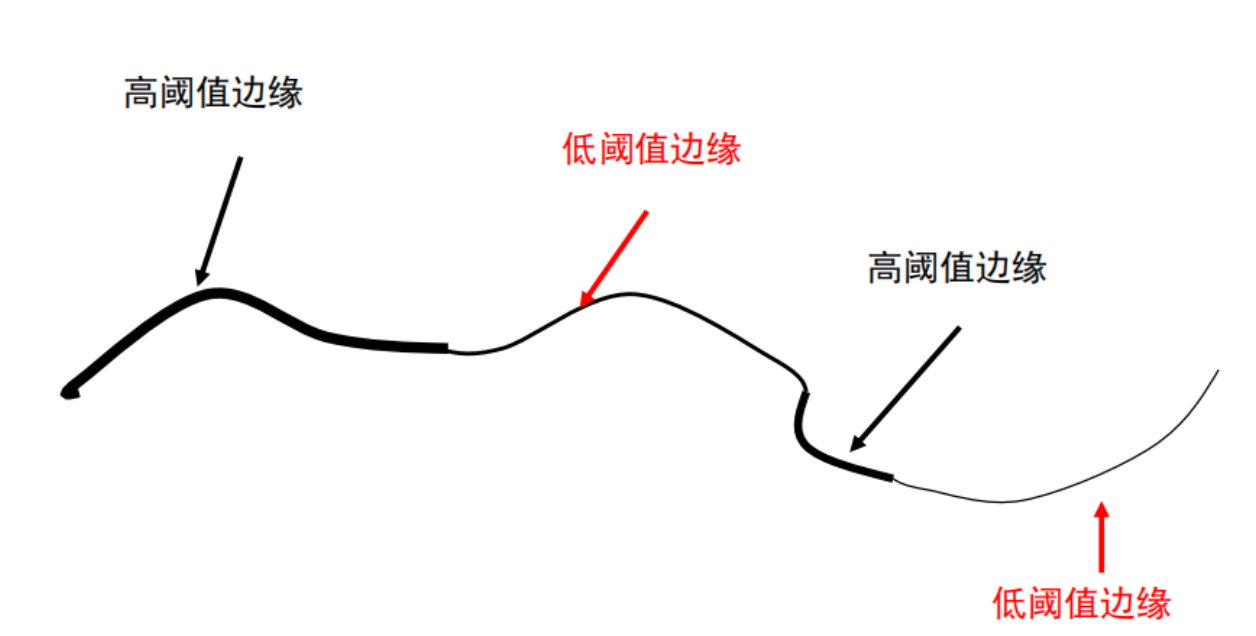
针对于幅值门限值设定的问题，Canny算法又提出了双阈值（门限值）的方法。也就是设定两个门限值，首先设定一个高门限值，将具有鲁棒性的边先提取出来，在设定一个低门限值，只有高于这个低门限值的边才会被提取，但是这必定会引入噪声边，那么这里就做了一个规定，就是必须是与高门限值边缘和低门限值边缘相连的那些边才能被留下来，这样就增加了最后提取边缘的鲁棒性。

上图是门限过高，门限过低，以及双门限的一个效果图。可以看到高门限过滤掉了一些有用的边，低门限加入了很多的噪声边，只有双门限的效果最好，首先通过高门限留下鲁棒性比较好的边，再利用低门限获取与鲁棒性比较好的边有关联的边。

7.4 Canny边缘检测器步骤总结

值得注意的是高斯一阶导滤波器做的事情只是告诉我们这个点是不是边缘点，或者是边缘点的可能性，并不会告诉我们真正的边缘点在哪里，也就是一个粗工序，得到的结果里面的边比较粗糙，并且可能有很多的噪声边。那么Canny算法做的事情，就是进一步细化边缘提取这一工序，会告诉我们准确的边在哪里，提出了两个比较重要的概念：非极大值抑制和双门限。