基于分治法的循环日程表算法

 问题描述：

1. 设有n=2k个运动员要进行羽毛球循环赛，现要设计一 个满足以下要求的比赛日程表：
2. 每个选手必须与其它n-1个选手各赛一次；
3. 每个选手一天只能比赛一次；
4. 循环赛一共需要进行n-1天。

需要注意的是：

• 由于n=2k，显然n为偶数。

采用分治策略求解的分析：

• 将所有的选手分为两半，n个选手的比赛日程表就可通 过为n/2个选手设计的比赛日程表来决定。
• 递归进行分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单

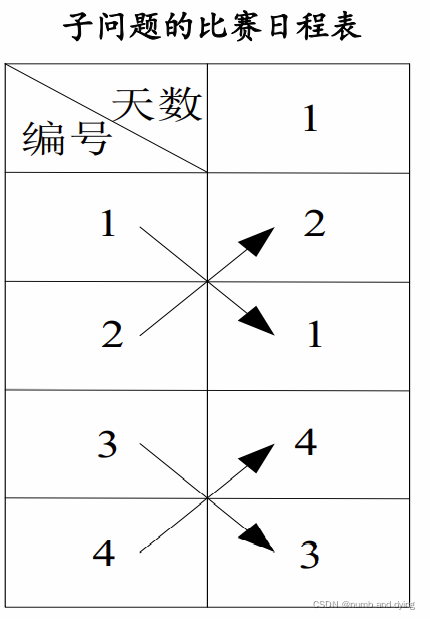
n=2^1个选手的比赛日程表的制定：

n=2^2个选手的比赛日程表的制定：

 

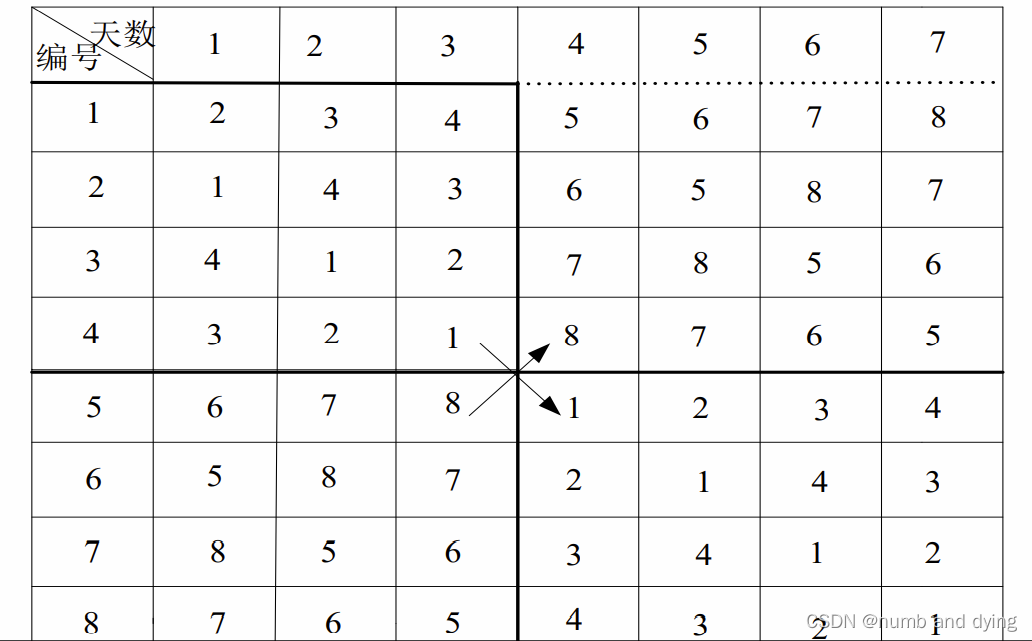
n=2^3个选手的比赛日程表的制定：

n=2^3个选手的比赛日程表：

 算法实现：

#include <iostream>
using namespace std;

void table( int k , int** a) {
	int n = 2;
	a[0][0] = 1; a[0][1] = 2;
	a[1][0] = 2; a[1][1] = 1;

	for (int t = 1; t < k; t++) {
		int temp = n;
		n *= 2;

		for (int i = temp; i < n; i++)  // 填写左下角元素
			for (int j = 0; j < temp; j++)
				a[i][j] = a[i - temp][j] + temp;  // 左下角元素和左上角元素的对应关系

		for (int i = 0; i < temp; i++)  // 填写右上角元素
			for (int j = temp; j < n; j++)
				a[i][j] = a[i + temp][j-temp];  // 右上角元素和左下角元素的对应关系

		for (int i = temp; i < n; i++)  // 填写右下角元素
			for (int j = temp; j < n; j++)
				a[i][j] = a[i - temp][j-temp];  // 右下角元素和左上角元素的对应关系
	}
}

int hanglie(int k) {
	int n = 1;
	for (int i = 1; i <= k; i++) {
		n *= 2;
	}
	return n;
}

int main() {

	cout << "开始执行了" << endl;
	int  k = 4;
	int n = hanglie(k);
	int** arr = new int* [n];
	for (int i = 0; i < n; i++) {
		arr[i] = new int[n];
		for (int j = 0; j < n; j++) {
			arr[i][j] = 0;
		}
	}
	cout << "开始进入函数了" << endl;
	table(k, arr);
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cout << arr[i][j] <<  " ";
		}
		cout << endl;
	}
	cout << "程序执行完了" << endl;

	return 0;
}

算法分析：

时间复杂度：