目录
一、图的定义和术语
- 图：顶点和边组成的多对多线性关系
- 完全图：图中每个顶点和剩余的 n-1个顶点直接相连，其中无向图最大边数n*(n-1)/2，有向图最大边数n*(n-1)
- 连通图：一条线把所有顶点连接起来，其中无向图和有向图最小边数n-1
- 出度和入度：无向图只有度（与该点相连的边数），有向图的出度（箭头指出去）、入度（箭头指向自己）
- 回路：第一个顶点和最后一个顶点相同
- 简单回路：回路的儿子
二、图的存储结构
1.邻接矩阵表示法
简单说：用二维数组存储图，横纵坐标表示顶点，数组的值为0表示不连通，1表示连通。
特点：
- 无向图对称，可压缩，压缩后存储空间为n*(n+1)/2
- 有向图不对称，存储空间为n*n
- 邻接矩阵适合无向稠密图
- 对于带有权值的无向网，把1改为距离，0改为无穷大，表示不可通行
- 时间复杂度O(n*n+n*e) , n为顶点的数目，e为边的数目
代码实现：
typedef struct
{
VertexType vexs[MAX_VERTEX_NUM]; // 顶点向量
ArcNode arcs [MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵
int vexnum,arcnum; // 图的当前顶点数和弧(边)数
}AdjMatrix; //邻接矩阵存储的图
2.邻接表表示法
为表中的每一个结点都建立一个单链表，其中单链表后面链接的元素为此结点到别的结点，如下图：
上图把a b c d e 作为表头结点，分别编号1~5，a能到达b和d，所以后面加上4 2，具体实现和单链表类似，向下的三角代表无别的结点了。
代码实现：
#define MAX_VERTEX_NUM 20 // 最大顶点个数
typedef struct ArcNode{
int adjvex; //该弧所指向顶点的位置
struct ArcNode *nextarc; //指示下一条边或弧的指针
OtherInfo info; // 与该弧相关的信息
} ArcNode;
typedef struct VertexNode {
VertexData data; //顶点信息
ArcNode *firstarc; //指向第一条依附该顶点的弧的指针
} VertexNode;
typedef struct{
VertexNode vertex[MAX_VERTEX_NUM]; // 邻接表 int vexnum, arcnum; // 图的当前顶点数和弧(边)数 GraphKind kind; // 图的种类标志} AdjList; //邻接表存储的图
- 有向图的逆邻接表取反就行了，比如1->2，取反就是2->1
- 邻接表适合有向稀疏图
- 时间复杂度O(n+e)
三、图的遍历
1.广度优先搜索BFS
就上图而言，广度遍历就是队列的熟练应用。首先，把与1相连的2 3存入队列，2出队，把和2相连的4 5存入队列，3出队，把和3相连的6 7存入队列，4出队，把和4相连的8存入队列，接下来5 6 7 8出队，没有和他们相连的，队列为空，遍历结束。出队的顺序，就是广度优先搜索的序列。
上面这个，按照队列方法可以自己试着写一下.
演示动态图：
编码实现：
void BFSTraverse(Graph G,Status(*Visit)(int v)){
//按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组visited。
for(v = 0;v<G.vexnum;++v) visited[v] = FALSE;
InitQueue(Q); //置空的辅助队列Q
for(v = 0; v<G.vexnum; ++v)
if(!Visited[v]){ //v尚未访问
visited[v] = TRUE; Visit(v);
EnQueue(Q,v); //v入队列
while(!QueueEmpty(Q)){
DeQueue(Q,u); //队头元素出队并置为u
for(w = FirstAdjVex(G,u); w>=0; w=NextAdjVex(G,u,w))
if(!Visited[w]){ //w为u的尚未访问的邻接顶点
Visited[w] = TRUE; Visit(w);
EnQueue(Q,W);
} //if
} //while
} //if
} //BFSTraverse
- 相当于树的层次遍历
- 时间复杂度对于邻接表O(n+e)，邻接矩阵O(n*n)
2.深度优先搜索DFS
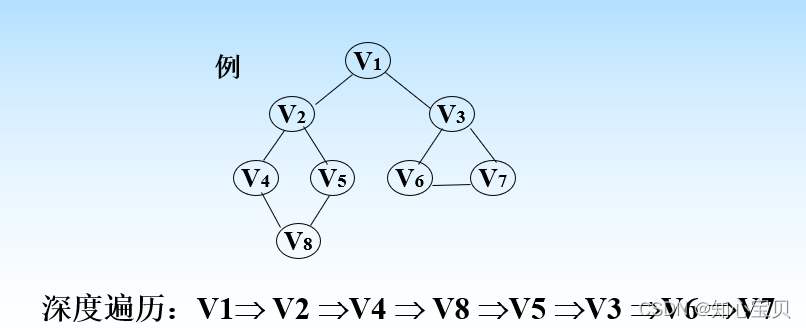
对于上面的图片，深度优先遍历貌似一条道走到黑，撞到墙会回头的算法。从1开始，->2->4->8->5 ，之后发现5只能到2，然而2却走过了，所以慢慢往回退，退到8 4 2都没有发现其它的路径。当退到1时发现1->3没有访问过，于是1->3->6->7直到所有的结点被访问完成。
演示视频：
编码实现：
Boolean visited[MAX]; //访问标志数组
Status(*VisitFunc)(int v); //函数变量
void DFSTraverse(Graph G,Status(*Visit)(int v)){
//对图G作深度优先遍历
VisitFunc = Visit; //使用全局变量VisitFunc，使DFS不必设函数指针参数
for(v = 0;v<G.vexnum;++v) visited[v] = FALSE; //访问标志数组初始化
for(v = 0;v<G.vexnum;++v)
if(!visited[v]) DFS(G,v); //对尚未访问的顶点调用DFS
} // 类似算法 7.3
void DFS(Graph G,int v){
//从第v个顶点出发递归地深度优先遍历图G。
visited[v] = TRUE; VisitFunc(v); //访问第v个顶点
for(w = FirstAdjVex(G,V); w>=0; w=NextAdjVex(G,v,w))
if(!visited[w]) DFS(G,w); //对v的尚未访问的邻接顶点w递归调用DFS
}
- 相当于树的先序遍历
- 时间复杂度对于邻接表O(n+e)，邻接矩阵O(n*n)
总结：DFS就像一只老鼠走迷宫，碰到墙壁会返回，而DFS就像放一大堆老鼠从一个点向四面八方走迷宫，到了墙壁，老鼠撞死就没了。
四、图的连通性
1.Prime算法最小生成树
从起点开始，找其相邻边中权值最小的边所连另一个顶点，再找与这两个顶点相邻边中权值最小的边所连第三个顶点，重复，扩展到所有顶点。
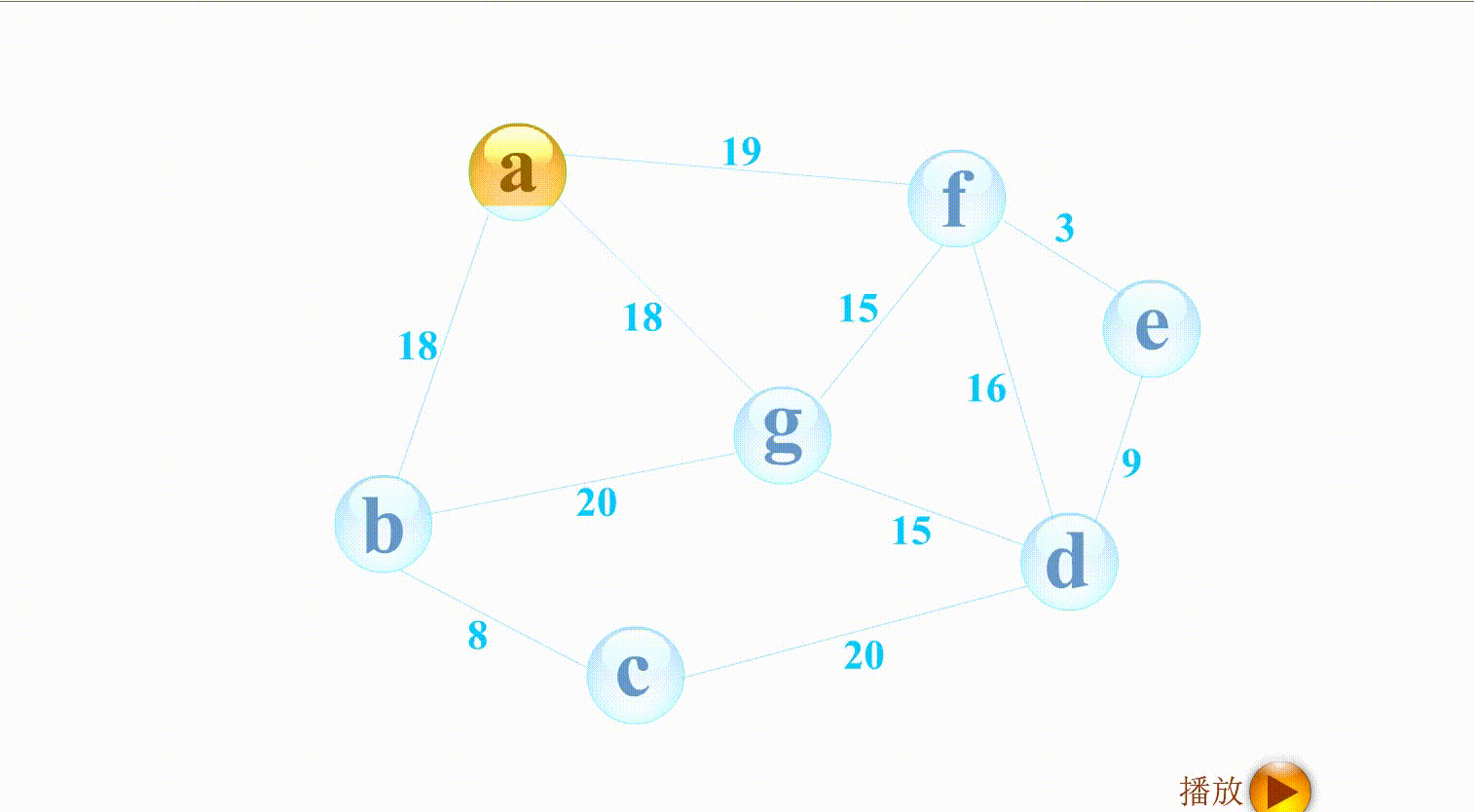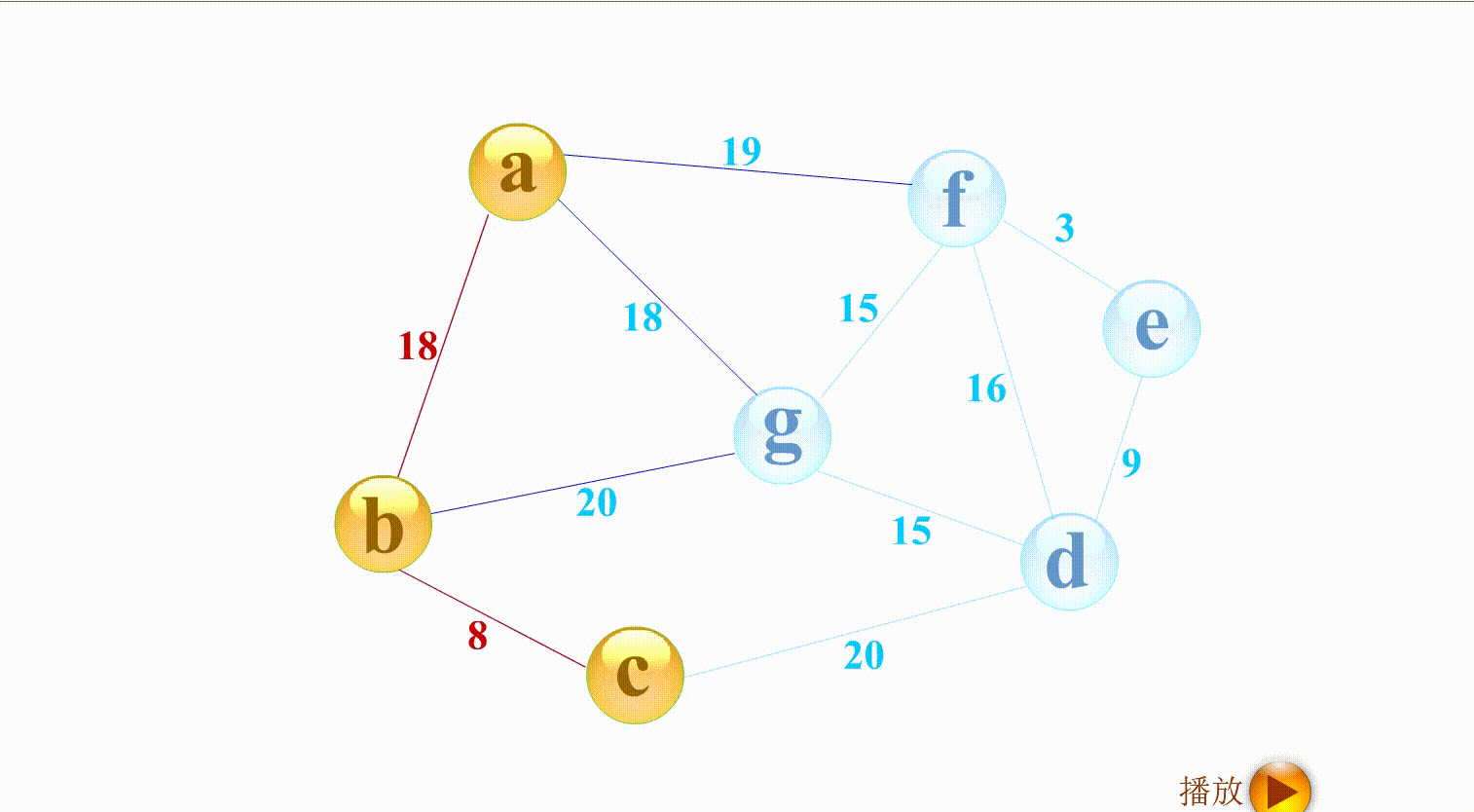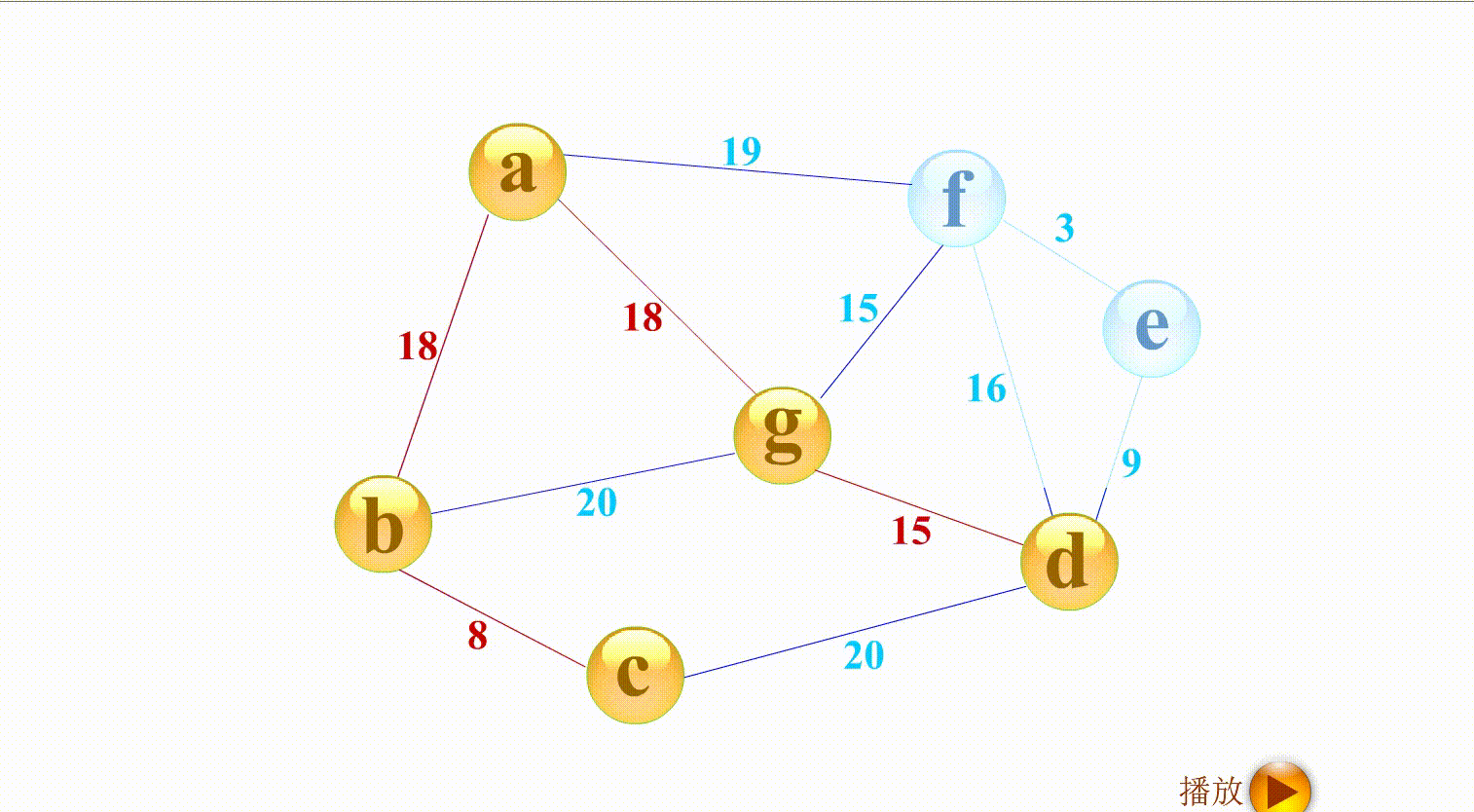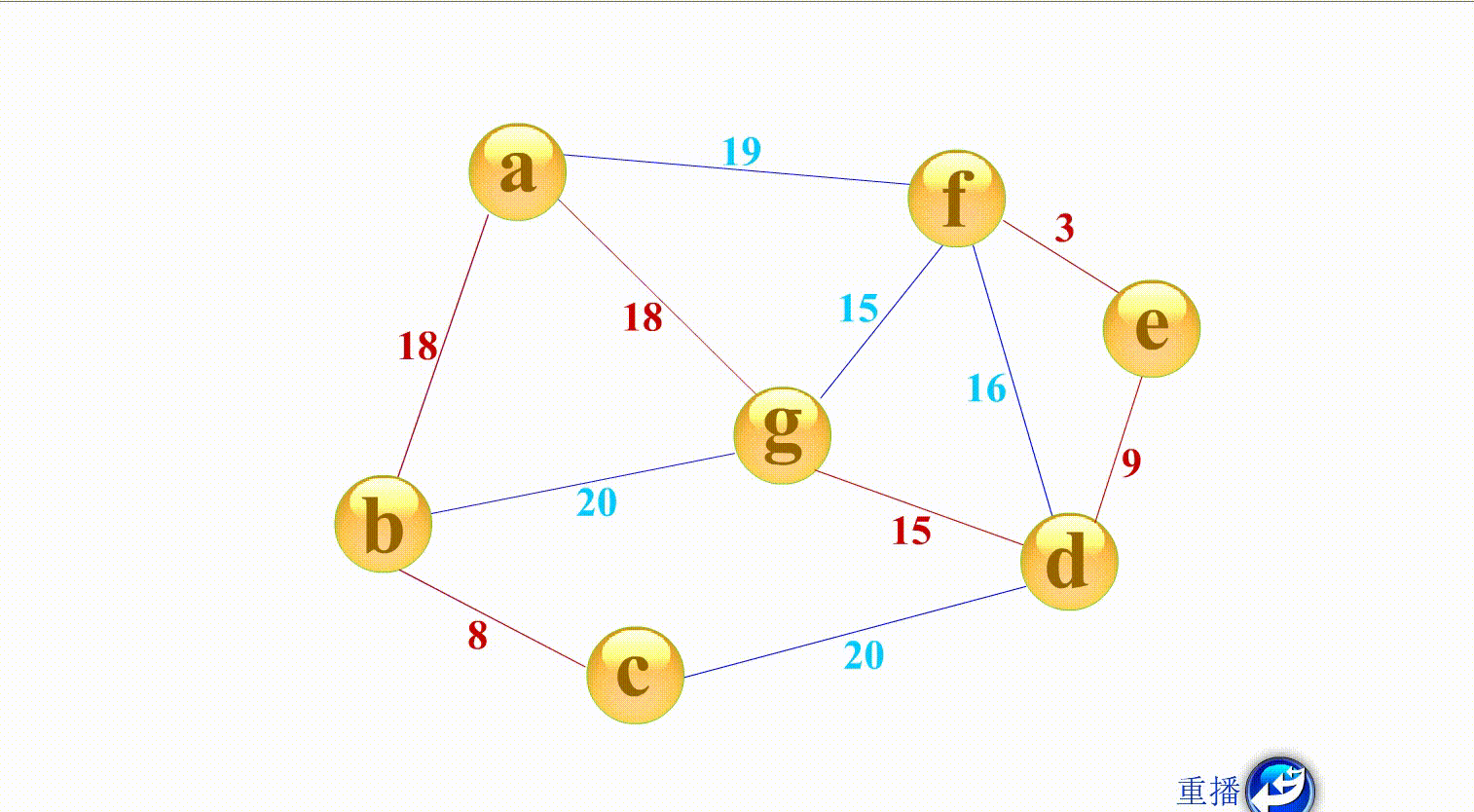
- Prime算法和广度搜索有点像，如上图，与 a相连的有b g f,权值最小的是b,与b相连的g c，权值最小的是c，以此类推
代码实现：
void MiniSpanTree_PRIM(MGraph G,VertexType u){
//用普里姆算法从第u个顶点出发构造网G的最小生成树T，输出T的各条边。
//记录从顶点集U到V-U的代价最小的边的辅助数组定义：
//struct{
// VertxtType adjvex;
// VRType lowcost;
// }closedge[MAX_VERTEX_NUM];
k = LocateVex(G,u);
for(j = 0;j<G.vexnum;++j) //辅助数组初始化
if(j! = K) closedge[j] = {u, G,arcs[k][j].adj}; //{adjvex, lowcost}
closedge[k].lowcost = 0; //初始，U = {u}
for(i=1;i<G.vexnum;++i){ //选择其余G.vexnum-1个顶点
k = minimum(closedge); //求出T的下一个结点：第k顶点
//此时closedge[k].lowcost =
// MIN{closedge[vi].lowcost|closedge[vi].lowcost>0,vi∈V-U}
printf(closedge[k].adjvex , G.vexs[k]); //输出生成树的边
closedge[k].lowcost = 0; //第k顶点并入U集
for(j = 0;j<G.vexnum;++j)
if(G.arcs[k][j].adj<closedge[j].lowcost) //新顶点并入U后重新选择最小边
closedge[j] = {G.vexs[k], G.arcs[k][j].adj};
}
}//MiniSpanTree2.克鲁斯卡尔算法最小生成树
先将所有顶点都看作无边的非连通图，选择各顶点间最小边做连通分量，直到所有定点都在同一个连通分量上。
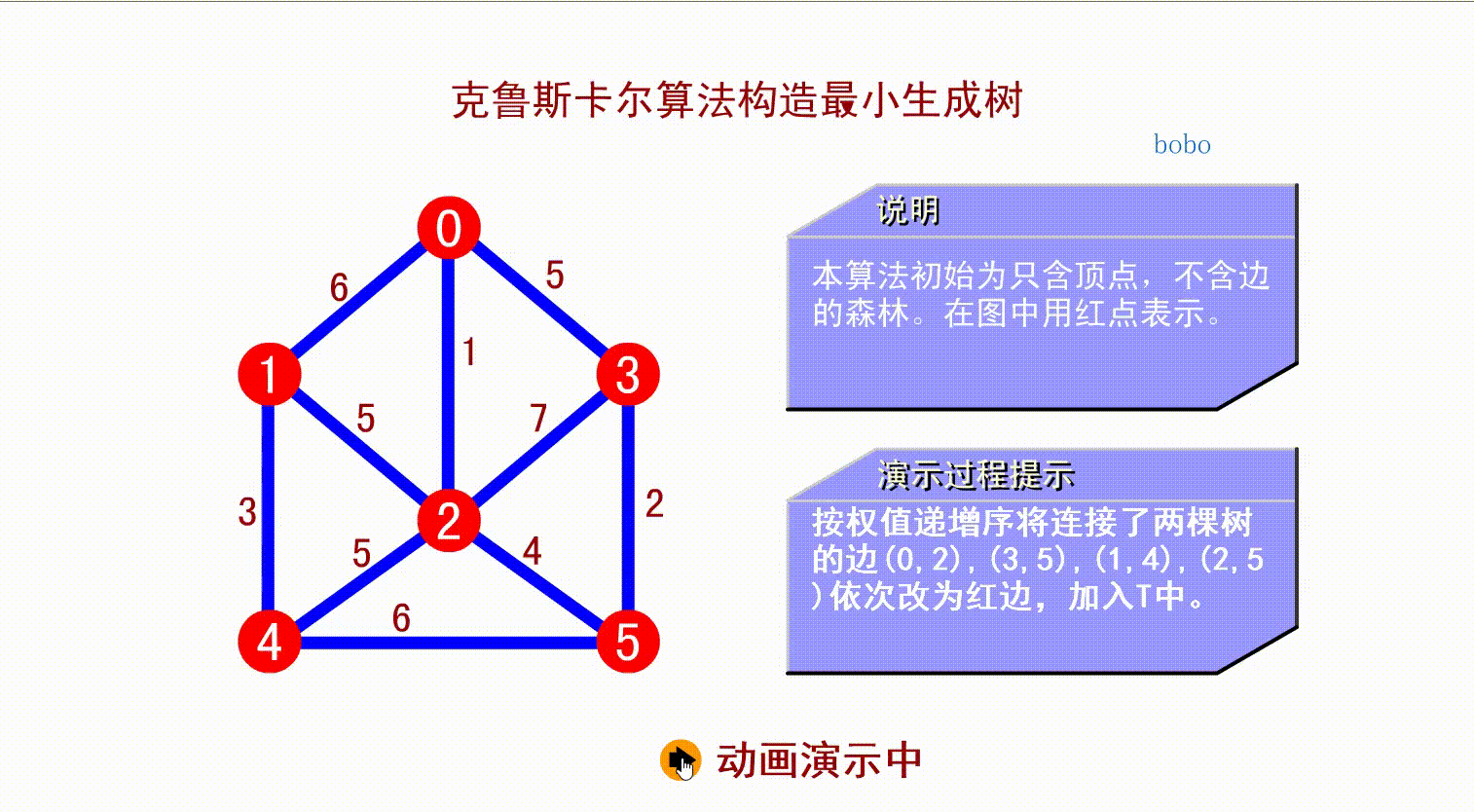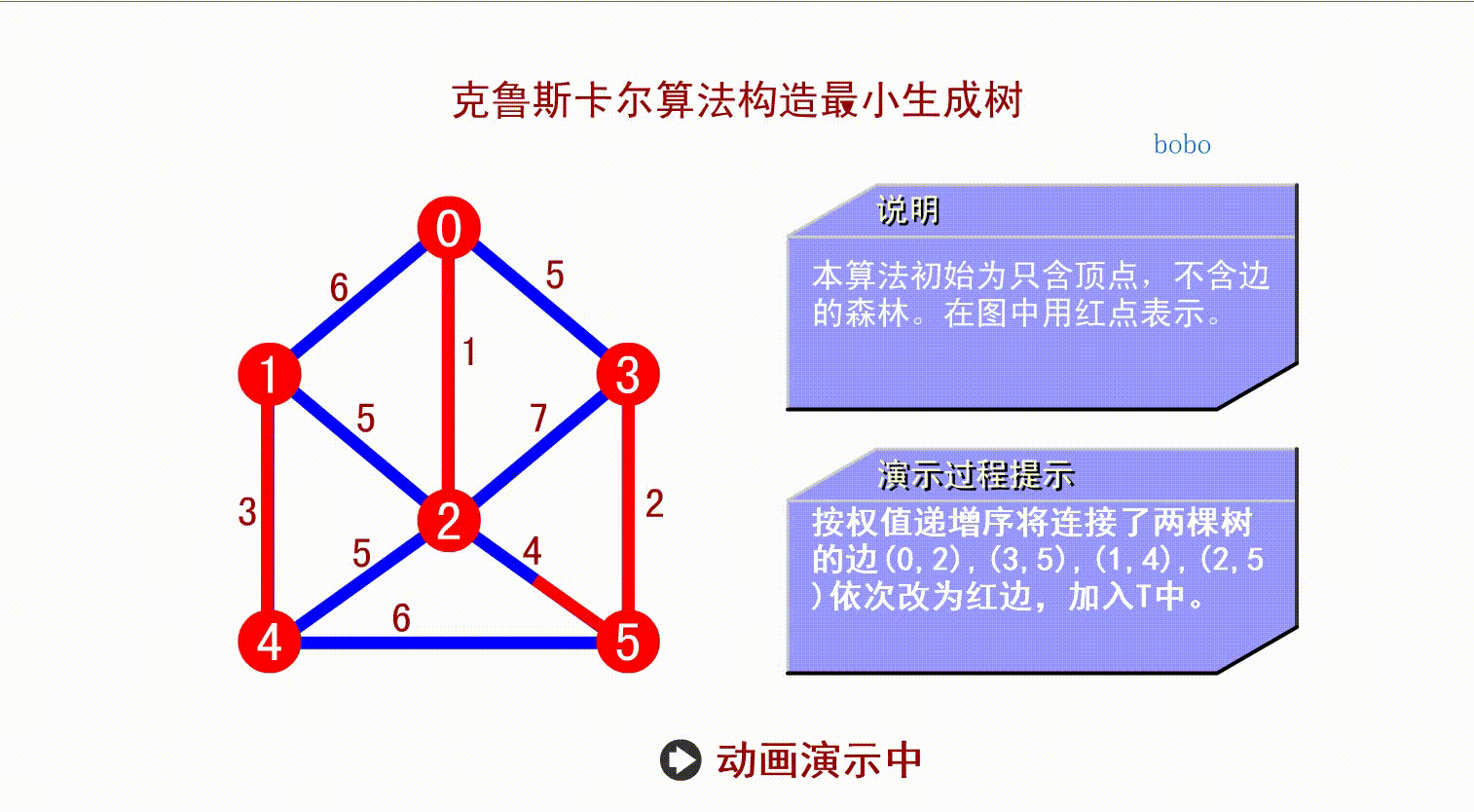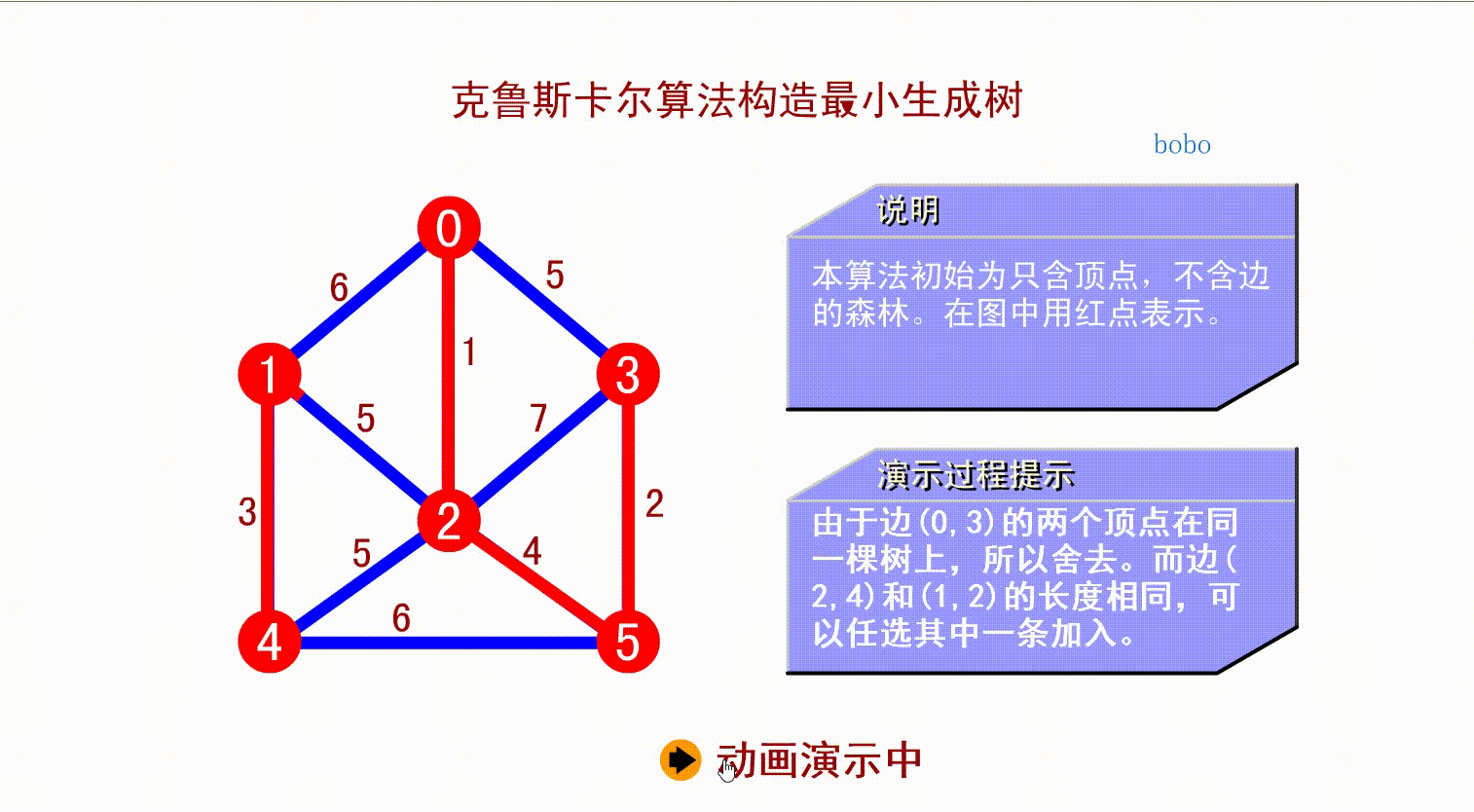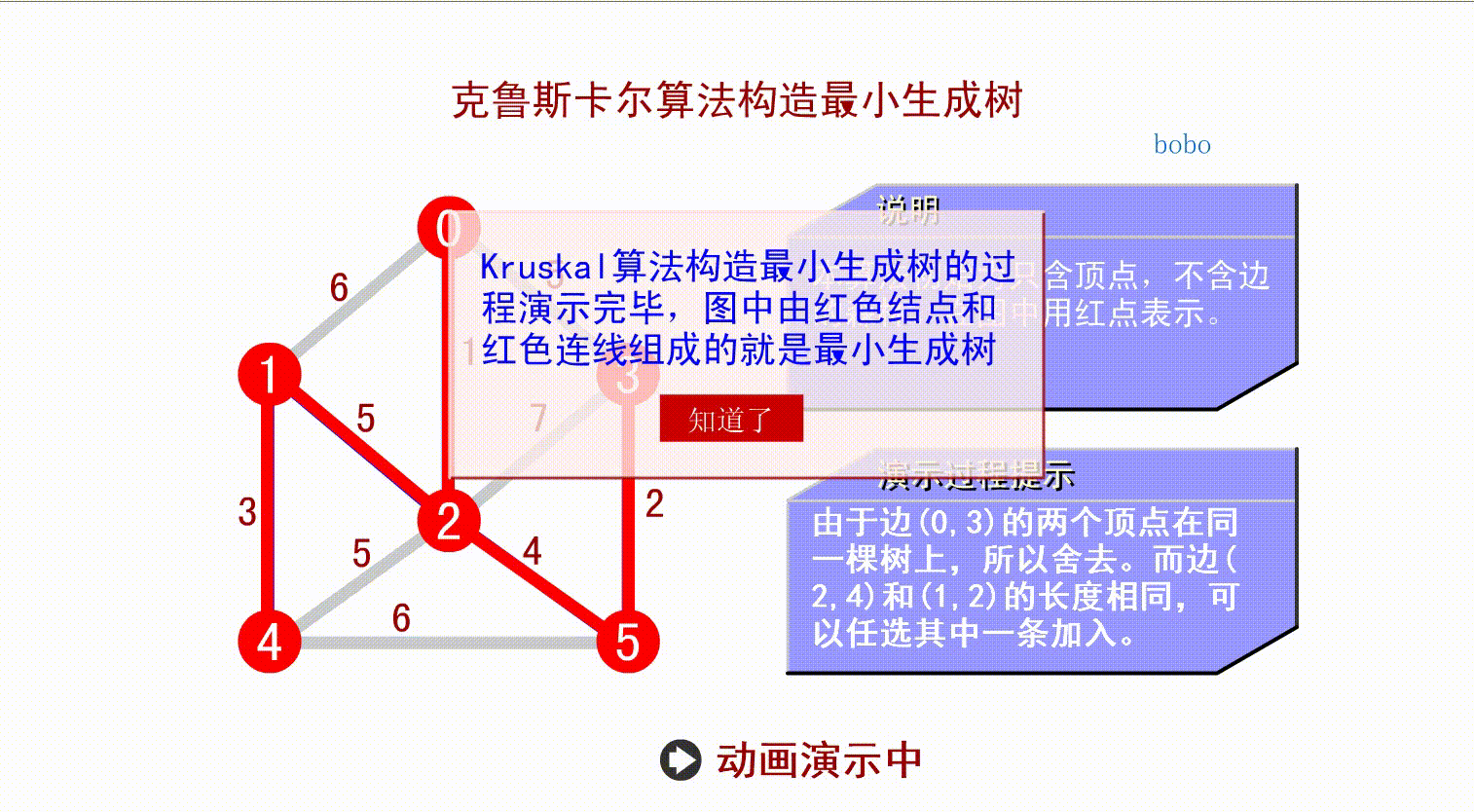如上面的算法演示，从小到大找到权值最小的边，连接两个顶点，只要不形成回路，就行，算法不作要求。
扫一扫
3220
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
