KalmanNet在轮式机器人集成导航中实现精确数据融合的实际应用（论文翻译和学习笔记）

摘要：扩展卡尔曼滤波器已广泛应用于传感器融合，以实现集成导航和定位。有效整合多个传感器需要对其误差有先验知识，以设置滤波器。最近出现的KalmanNet成功地利用循环神经网络从数据中学习先验知识，并在部分信息下对非线性动态问题进行状态估计。在本文中，KalmanNet被应用于使用GPS/轮速和惯性测量单元的数据进行集成导航。文中提出了一种通过利用卡尔曼滤波器系统状态的一阶马尔可夫性质来改进截断时间反向传播训练算法的实用策略，从而提升现有KalmanNet的训练稳健性和性能。在密歇根NCLT数据集上的实验结果表明，我们的融合KalmanNet在平均均方根误差（RMSE）上显著优于传统的基于扩展卡尔曼滤波器的融合算法，改善幅度为20%至40%。

关键词：集成导航和定位  卡尔曼滤波器  循环神经网络  传感器融合

作者：Jian Song , Wei Mei , Yunfeng Xu , Qiang Fu , and Lina Bu

0  前言*

        导航和定位系统广泛应用于航空航天、智能农业和车辆导航等多个领域，并在近年来吸引了大量研究[1,2,3,4,5,6]。在车辆导航中，通常利用各种测量系统，例如惯性测量单元（Inertial Measurement Unit, IMU）、轮编码器（Wheels）和GPS，以实现性能增强的集成导航。每种传感器都有其独特的特性。GPS通常具有较高的精度，但在存在遮挡效应和多径传播的情况下可能会降低性能[7]；IMU和轮编码器是一类航位推算传感器，可以提供车辆的相对位置，但其定位误差会随时间漂移[8]。为了实现集成导航，扩展卡尔曼滤波器（Extended Kalman Filter, EKF）通常作为主流技术，用于融合来自一组传感器的信息[1,2,9,10,11,12]。基于EKF的融合算法要求滤波器参数的设置必须准确，以适应传感器的噪声分布。在[13]中，作者展示了一个不正确的滤波器参数可能导致导航解，包括姿态，快速发散。最近，数据辅助滤波技术，如KalmanNet，作为一种高效的方法出现，用于处理具有部分信息的非线性动态下的估计问题。KalmanNet的整体结构与卡尔曼滤波器（Kalman Filter, KF）相似。唯一的区别在于KalmanNet利用循环神经网络（Recurrent Neural Networks, RNNs）而不是解析模型，从输入特征（如测量残差）中学习卡尔曼增益（Kalman Gain, KG），从而获得克服模型不匹配和非线性的能力。然而，在我们的工作中观察到，当模型不匹配严重时，KalmanNet在训练中可能快速发散并导致非数（Not a Number, NaN）。

        在本论文中，主要贡献包括两点：

        (1)成功实现了KalmanNet及其变体，以不同的数据速率进行传感器融合。

        (2)基于KF系统状态的一阶马尔可夫性质，提出了一种更适用于KalmanNet的训练方法，以增强其训练稳定性。

        对密歇根NCLT数据集的实验结果显示，所实现的KalmanNet显著优于传统的基于EKF的融合算法，平均均方根误差（Root Mean Square Error, RMSE）提高了20%至40%，而采用的训练方法可以减少现有KalmanNet在模型不匹配场景中的训练难度，同时提升其性能。本文的其余部分安排如下：第二部分介绍传感器融合任务和提出的方法；第三部分给出实际数据集的实验结果；第四部分呈现结论。

1  研究方法

1.1  系统模型

考虑一个通过离散时间非线性状态空间模型表示的情况

图1  EKF/KalmanNet传感器融合的流程图

1.2  扩展卡尔曼滤波器用于传感器融合

        我们考虑一种基于扩展卡尔曼滤波（EKF）的松耦合传感器融合算法，该算法用于融合具有不同数据速率的传感器数据，并估计当前位置信息。根据(1)、(2)模型，该算法可以定义为两个阶段：预测和校正。如图1所示，这两个阶段对应于不同的传感器。预测阶段通常对更新频率高但准确率低的传感器建模，例如惯性测量单元（IMU）/车轮编码器，而校正阶段则对更新频率低但准确率高的传感器建模，例如全球定位系统（GPS）。这种松耦合策略确保在GPS信号丢失时仍能保持稳定的位置信息估计。

1.3  GPS-IMU/轮速数据融合

1.4  KalmanNet用于传感器融合

        考虑在传感器融合应用中用KalmanNet[14]或其变体Split-KalmanNet[15]替代扩展卡尔曼滤波器（EKF）。它们是一类混合方法，旨在将深度神经网络（DNNs）整合到卡尔曼滤波器（KF）中，同时保持KF的核心结构，从而在存在模型不匹配时实现稳健的状态估计。

1.5  KalmanNet的实用训练策略

        我们对KalmanNet的实现采用了一种实用的训练策略，这有效提高了其训练的稳健性，并带来了额外的性能提升。KalmanNet通常使用截断的反向传播通过时间（TBPTT）进行训练，该方法将总长度为T的序列拆分为M个长度为D的序列，并将每个长度为D的序列视为相互独立的训练样本。该算法更像是截断的“序列”反向传播通过时间（BPTT），在大多数情况下表现良好。然而，这个算法可能使KalmanNet出现问题：(1)当D较大时，由于模型严重不匹配，KalmanNet潜在的梯度爆炸问题可能变得更加严重，导致出现NaN。(2)当D较小时，限制了网络能够学习的时间尺度。

表1  不同方法在测试数据集上的米级均方根误差（RMSE）

Tab.1  The meter-level root mean square error (RMSE) of different methods on the test data set.

        这样做有几个优点：

        (1) 每个序列多次更新权重（即，w<D）缓解了KalmanNet因模型不匹配而导致的训练问题。这使我们能够使用相对较大的D，从而增加网络可以学习的时间尺度。

        (2) 每次权重的更新仅依赖于最近几个时间步生成的梯度（例如，k=2），这使得模型主要关注来自最近时间步的输入信息。

        (3) 由于D≥k且D≥w，网络的记忆容量并不受k和w的限制。相反，适当的k和w可以减轻梯度消失现象，并更全面地利用输入信息。

2  实验结果

本实验使用密歇根NCLT数据集来评估KalmanNet及其变体在传感器融合中的性能。

2.1  实验设置

(1) 数据集描述：NCLT数据集由Segway机器人平台收集的数据组成。它包含27条轨迹，每条轨迹提供来自传感器的数据，例如消费级GPS（5 Hz）、轮编码器（37 Hz）和IMU（47 Hz），以及真实值（100 Hz）[12,16]。

(2) 数据处理：27条轨迹随机分为三个部分：22条用于训练，2条用于验证，3条用于测试。经过1 Hz的采样后，训练、验证和测试轨迹的平均长度分别为5040、2917和4644。

(3) 对比模型：EKF：遵循[12]中的设置，该设置源于传感器的参数。KalmanNet和Split-KalmanNet：模型和训练策略在II-D和II-E节中讨论。

(4) 超参数设置：在实验中，KalmanNet及其变种使用相同的超参数进行训练，轮数、批量大小和学习率分别为50、256和0.001。为了验证算法在KalmanNet上的有效性，我们在多个设置下进行训练，k=2，w∈{4,8}，D∈{50,100,200}。

(5) 评估指标：使用均方根误差（RMSE）来评估某条轨迹，以及测试数据集中所有轨迹的平均RMSE。

2.2  实验结果

        表1给出了EKF和KalmanNets在测试数据集上的比较结果，而表2则展示了KalmanNet和Split-KalmanNet在不同 TBPTT(k, w, D)设置下的性能。“仅GPS”意味着位置是通过使用原始 GPS 测量值来给出的。“仅轮子”仅使用轮编码器的数据进行预测，而不进行任何来自GPS的修正。“轮速加 GPS”表示使用预测和修正估计的位置。

        从表1可以看出，KalmanNet的平均RMSE为8.01米，较“仅GPS”提高了75%，较“带GPS的轮速EKF”提高了39%。虽然Split-KalmanNet 稍逊于KalmanNet，但在平均RMSE上仍然对“仅GPS”和“带GPS的轮速EKF”分别提高了73%和34%。图2显示了KalmanNet、EKF和GPS的结果，以及2012-11-16测试路径的真实值。可以看出，对于集成导航任务，KalmanNet能够将EKF的估计误差从12.29米减少到5.60米。图2右侧的放大视图显示，当轮式机器人在室内导航且GPS信号通常不可用时，KalmanNet相较于EKF的优势尤为明显。实验验证了传感器融合的必要性以及KalmanNet在传感器融合方面的卓越表现。

        从表2可以看出，使用我们策略训练的KalmanNet和SplitKalmanNet在D=50、100和200时优于原始版本（k=w=D）。具体而言，我们的方法现在能够有效地训练长轨迹。例如，在较大的D=100或200时，由于模型不匹配导致的NaN，KalmanNet在使用原始的TBPTT情景下变得难以训练。相比之下，当w∈{4,8}时，KalmanNet仍能表现良好。与此同时，在较小的D=50时，KalmanNet和Split-KalmanNet的平均RMSE分别降至8.01米和9.62米，分别提高了28%和46%相较于TBPTT(50,50,50)。这些实验表明，我们的训练策略在降低现有KalmanNet的训练难度和提高其性能方面的有效性。这样的改进得益于滑动窗口机制和k步梯度分离。滑动窗口的采用增强了网络学习的时间尺度。成功在较小的k=2上的应用表明，KalmanNet仅需短期交互即可捕捉由系统状态的一级马尔可夫性质所支配的序列中的依赖关系。

图2  实验结果

Fig.2 Experimental results

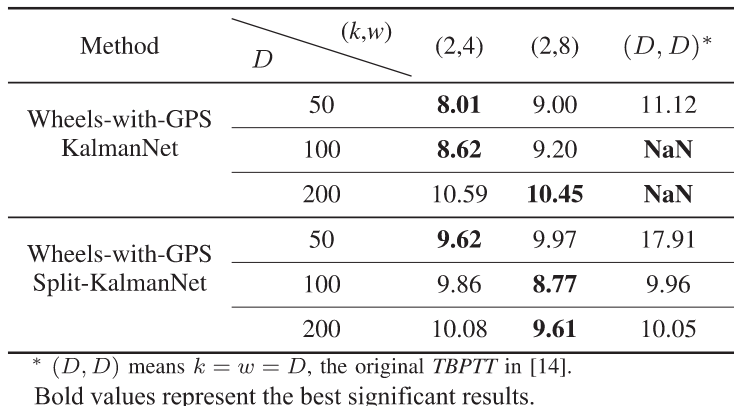
表2  不同 TBPTT 设置下测试数据集的平均 RMSE（以米为单位）

Tab.2  The average RMSE (measured in meters) of the test dataset under different TBPTT settings.

3  结论

        在本文中，我们提出了一种更适用于KalmanNets的训练方法，以增强其训练稳定性和性能。该方法使用滑动窗口在每个序列中多次更新循环神经网络的权重，从而扩展了网络学习的时间尺度。考虑到系统状态的马尔可夫性质，每次权重的更新仅依赖于最近几个时间步生成的梯度。对NCLT真实数据集的实验结果证明了我们的方法在综合导航任务中的有效性。

参考文献

[1] XU Y J, ZHAO X H, LIANG Y C. Robust power control and beamforming in cognitive radio networks: a survey[J].IEEE Communications Surveys & Tutorials, 2015, 17(4): 1834-1857.

[2] ZHANG M, CUMANAN K, BURR A. Energy efficiency optimization for secure transmission in miso cognitive radio network with energy harvesting[J]. IEEE Access, doi: 10.1109/ACCESS.2019.2938874, 2019.

[3] MANSUKHANI J, RAY P. Censored spectrum sharing strategy for mimo systems in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2019，18（12）：5500-5510.

[4] HAYKIN S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220.

[5] XU Y J, HU Y, CHEN Q B, et al. Optimal power allocation for multiuser OFDM-based cognitive heterogeneous networks[J]. China Communications, 2017, 14(9): 52-61.

[6] XU H, LI B. Resource allocation with flexible channel cooperation in cognitive radio networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(5): 957-970.

[7] NI Q, ZARAKOVITIS C C. Nash bargaining game theoretic scheduling for joint channel and power allocation in cognitive radio systems[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(1): 70-81.

[8] ILLANKO K, NAEEM M, ANPALAGAN A, et al. Energy efficient frequency and power allocation for cognitive radios in television systems[J]. IEEE Systems Journal, 2016, 10(1): 313-324.

[9] XU C, SHENG M, YANG C, et al. Pricing-based multi resource allocation in OFDMA cognitive radio networks: an energy efficiency perspective[J]. IEEE Transactions on Vehicular Technology, 2014, 63(5): 2336-2348.

[10] GAO S, QIAN L, VAMAN D R. Distributed energy efficient spectrum access in cognitive radio wireless Ad hoc networks[J]. IEEE Transactions on Wireless Communications, 2009, 8(10): 5202-5213.

[11] PAUL A, BANERJEE A, MAITY S P. Residual energy maximization in cognitive radio networks with Q-routing[J]. IEEE Systems Journal, doi: 10.1109/JSYS T.2019.2926120, 2019.

[12] XU Y J, LI G Q. Optimal and robust interference efficiency maximization for multicell heterogeneous networks[J]. IEEE Access, 2019, 7: 102406-102416.

[13] MILI M R, MUSAVIAN L. Interference Efficiency: a new metric to analyze the performance of cognitive radio networks[J] IEEE Transactions on Wireless Communications, 2017, 16(4): 2123-2138.

[14] DINKELBACH W. On nonlinear fractional programming[J]. Management Science, 1967, 13: 492-498.

[15] XU Y J, ZHAO X H. Robust power control for underlay cognitive radio networks under probabilistic quality of service and interference constraints[J]. IET Communications, 2014, 8(18): 3333-3340.

[16] 徐勇军,胡圆,李国权,等.异构携能通信网络顽健资源分配算法[J]. 通信学报, 2019, 40(7):186-196.

XU Y J, HU Y, LI G Q, et al. Robust resource allocation algorithm for heterogeneous wireless networks with SWIPT[J]. Journal on Communications, 2019, 40(7):186-196.

[17] OLFAT M, FARROKHI R F, LIU K J. Power allocation for OFDM using adaptive beamforming over wireless networks[J]. IEEE Transactions on Communications, 2005, 53(3): 505-514.

[18] SETOODEH P, HAYKIN S. Robust transmit power control for cognitive radio[J]. Proceedings of the IEEE, 2009, 97(5): 915-939.