欧几里得
这人是真的厉害!
辗转相除法
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int gcd(int a, int b) // 欧几里得算法,a非负,
{
return b ? gcd(b, a % b) : a;
}
int main()
{
int a,b;
cin >> a >> b;
cout <<gcd(a,b);
return 0;
}
定理
gcd(a,b) = gcd(b,a mod b);
证明
- a可以表示成a = kb + r,则 r = a mod b;
- r = a - kb则a = r mod b;
- 易得 gcd(a,b) = gcd(b,a mod b);
扩展欧几里得
扩展欧几里得算法的描述是:一定存在整数 x, y 满足等式 a * x + b * y = gcd(a,b)
这里的a,b是已知,gcd(a,b)表示的是a和b的最大公约数,所以扩展欧几里得算法既可以计算出最大公约数gcd(a,b),又可以计算出变量x,y的一组解。如何求解呢?
计算最大公约数的下一步,带入等式:gcd(b, a % b) = bx1 + (a % b) * y
即就是:gcd(b, a % b) = bx1 + (a - (a / b) * b) * y1
gcd(b, a % b) = a * y1 + b * (x1 - (a / b) * y1 )
在回过头来看看等式 当b不等于0时:gcd(a,b) = gcd(b,a%b)
所以,x = y1 ; y = x1 - (a / b) * y1
所以可以递归的求解x,y。那退出条件是什么呢?
我们可以看到当b == 0时,求出最大公约数。考虑一下当b == 0时,a * x = gcd(a, 0) = a。
此时,x == 1,y取0即可计算出一组特解。
普通版
int exgcd(int a, int b, int& x, int& y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int temp = y;
y = x - (a / b) * y;
x = temp;
return d;
}
升级版
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
扩展欧几里得算法可以计算二元一次方程组是否存在整数解,并且求出一组解
欧几里得算法只能用来求整数解(因为最大公约数的缘故)
二元一次方程:ax + by = c
1)当a == 0 或 b == 0的时候,方程转为一元一次方程,可直接求得。
2)当c不是 gcd(a,b)的倍数的时候,方程无解。
因为a和b都是他因子的倍数,这个毫无疑问,所以ax+by(a, b的线性组合)也是gcd(a, b)的倍数。如果c不是gcd(a, b)的倍数,那么两边不相等,无解。这条结论叫做“裴蜀定理”。
3)当c是gcd(a, b)的倍数,设g = gcd(a, b),则用ax + by = g求解出的一组解(x0,y0),有ax + by = c 求出的一组解为(x0c/g,y0c/g)
如果你理解了,可以挑战一下 青蛙的约会 这道题。
题解:http://blog.csdn.net/SwordHoly/archive/2009/08/07/4423543.aspx可以参考一下
用扩展欧几里得算法求乘法逆元
这里先说一下乘法逆元,我们都知道,‘取模%’ 具有加、减、乘法的分配率即:
1). (a+b) % c = ((a%c) + (b%c))%c
2). (a-b) % c = ((a%c) - (b%c))%c
3). (a× \times×b) % c = ((a%c)× \times× (b%c))%c
这样的好处就是,如果a+b+…+n计算出来的值太大的话,可以通过分配率来计算出每一步的值在求余。
除法没有分配率,但是有乘法逆元。就是将除法转化为乘法。
逆元:设c是b的逆元,则有ax ≡ \equiv≡ 1(mod p);
(a/b)mod p = (a/b) * 1(mod p) = (a/b)bx (mod p) = ax(mod p)
定理:a存在模p的乘法逆元的充要条件是gcd(a,p) = 1;(定理的证明在这里就不叙述了)
对于ax + by = 1,可以看出x是a模b的乘法逆元,y是b模a的乘法逆元。
中国剩余定理(孙子定理)利用乘法逆元
中国剩余定理这样描述,给出以下一元线性同余方程组
给出你n个ai和mi,求出符合题意的X值,一般输出最小解。
ti 要用扩展欧几里得算法e_gcd()计算。
一元线性同余方程组问题最早可见于中国南北朝时期(公元5世纪)的数学著作《 孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
即,一个整数除以三余二,除以五余三,除以七余二,求这个整数。《 孙子算经》中首次提到了同余方程组问题,以及以上具体问题的解法,因此在中文数学文献中也会将中国剩余定理称为孙子定理。
宋朝数学家 秦九韶于1247年《 数书九章》卷一、二《大衍类》对“物不知数”问题做出了完整系统的解答。明朝数学家 程大位将解法编成易于上口的《孙子歌诀》:
三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五使得知
这个歌诀给出了模数为3、5、7时候的同余方程的秦九韶解法。意思是:将除以3得到的余数乘以70,将除以5得到的余数乘以21,将除以7得到的余数乘以15,全部加起来后减去105(或者105的倍数),得到的余数就是答案。比如说在以上的物不知数问题里面,按歌诀求出的结果就是23。
例题中三个模数 m1=3,m2=5,m3=7;
余数a1=2,a2=3,a3=2;
M=105,M1=35 , M2=21,M3=15;
t1=2,t2=1,t3=1;
70=t1M1,21=t2M2,15=t3*M3
X =( a1 * t1 * M1 + a2 * t2 * M2 + a3 * t3 * M3)%M=( 2 * 2 * 35 + 3 * 1 * 21 + 2 * 2 * 15)%105=23
适用于n个mi两两互质的情况。
代码
//n个mi互质
ll m[101];ll a[101];//m[]存放互质的数,a[]存放余数
void e_gcd(ll a,ll b,ll &x, ll &y){//计算逆元
if(b==0){
x=1;y=0;return;
}
e_gcd(b,a%b,x,y);
ll temp=x;
x=y;
y=temp-a/b*y;
}
ll CRT(){
ll M=1;
for(int i=0;i<n;i++) M*=m[i];
ll ret=0;
for(int i=0;i<n;i++){
ll x,y;
ll tm=M/m[i];//计算Mi
e_gcd(tm,m[i],x,y);//计算逆元x
ret=(ret+x*a[i]*tm)%M;//计算结果值
}
return (ret+M)%M;
}

126 x 2 +225 x 2 + 280 x 4 = 247 (mod 315)







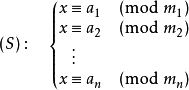















 4533
4533











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








