原码、反码、补码、移码及其算数移位

原码、反码、补码、移码转化总结

---

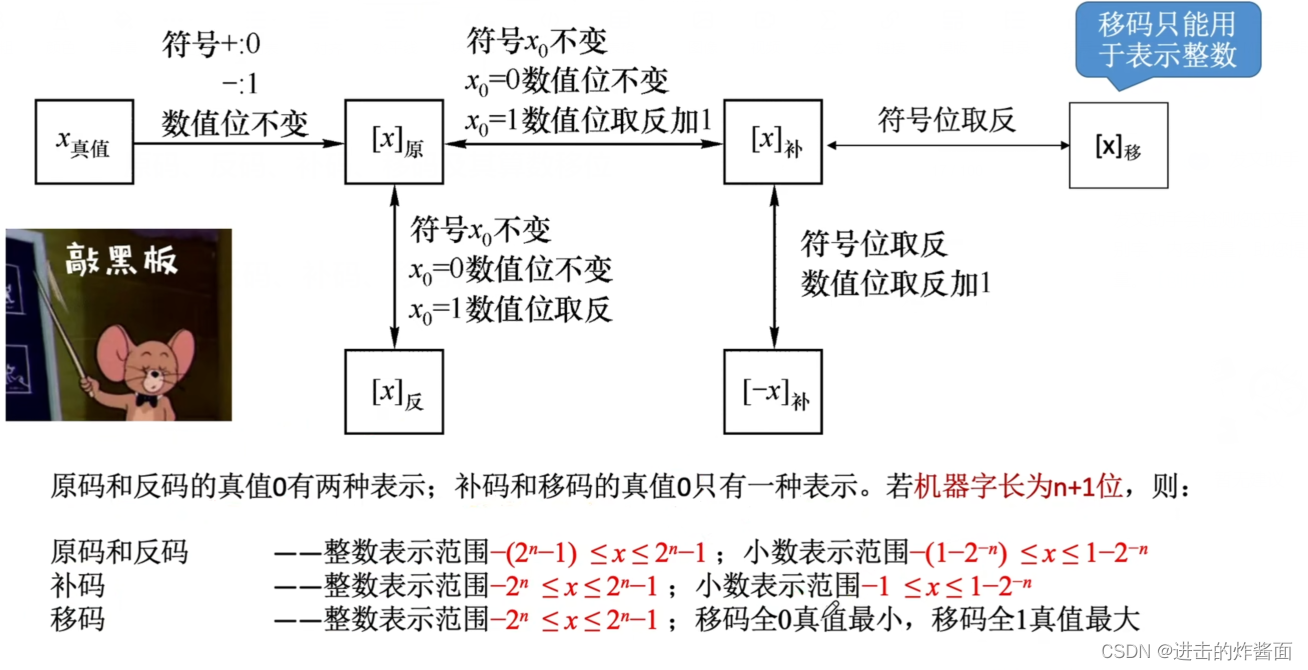
原码的算数移位--符号位不变，对数值位进行移位

右移：高位补0，低位舍弃。若舍弃的位=0，则相当于➗2；若舍弃的位≠0，则会丢失精度

左移：低位补0，高位舍弃。若舍弃的位=0，则相当于✖2；若舍弃的位≠0，则会产生严重误差

 

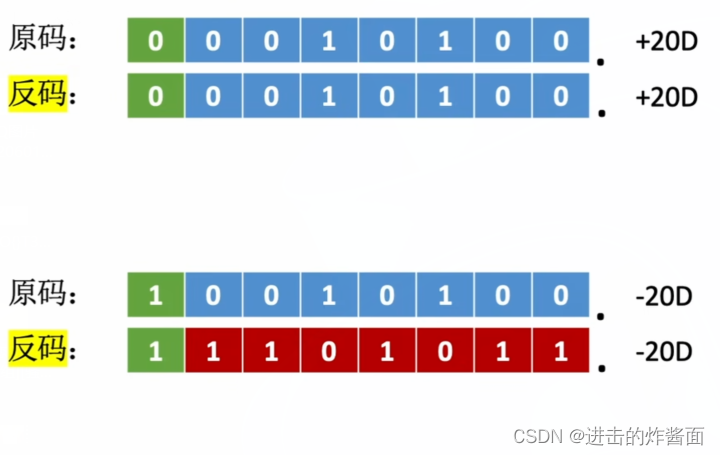
反码的算数移位

正数的反码与原码相同，因此对正数反码的移位运算也和原码相同。

负数的反码数值位与原码相反，因此负数反码的移位运算规则如下：

        右移：高位补1，低位舍弃

        左移：低位补1，高位舍弃

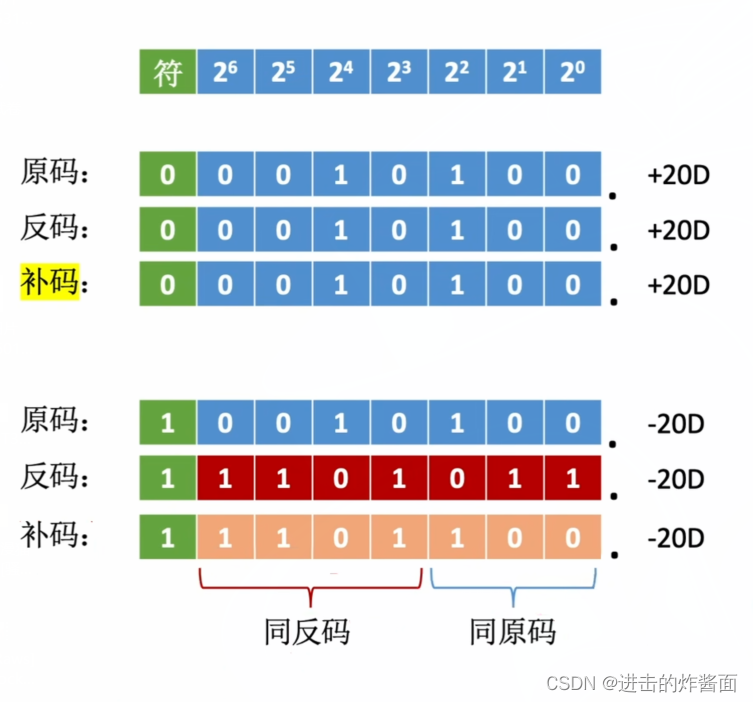
 补码的算数移位

正数的补码与原码相同，因此对正数补码的移位运算也和原码相同。

        右移：高位补0，低位舍弃

        左移：低位补0，高位舍弃

负数补码中，最右边的1及其右边同原码。最右边的1的左边同反码

移位规则如下：

右移（同反码）：高位补1，低位舍弃

左移（同原码）：低位补0，高位舍弃

原因：

        负数补码=反码末位+1 导致反码最右边几个连续的1都因进位而变为0，直到进位碰到第一个0为止。

 算数移位总结

 逻辑移位

逻辑右移：高位补0，低位舍弃

逻辑左移：低位补0，高位舍弃

可以把逻辑移位看作是对“无符号数”的算数移位

 循环移位