SVPWM算法原理及详解及永磁同步电机坐标变换（一）

目录

一、永磁同步电机基本结构

二、坐标变换（为后续SVPWM的内容做准备）

1. abc三相静止坐标系（3s坐标系）：

2. αβ两相静止坐标系（2s坐标系）：

3. dq两相旋转坐标系（2r坐标系）：

4. Clarke变换：

5. Clarke逆变换（IClarke）：

6. Park变换：

7. Park逆变换（IPark）：

---

 

 

一、永磁同步电机基本结构

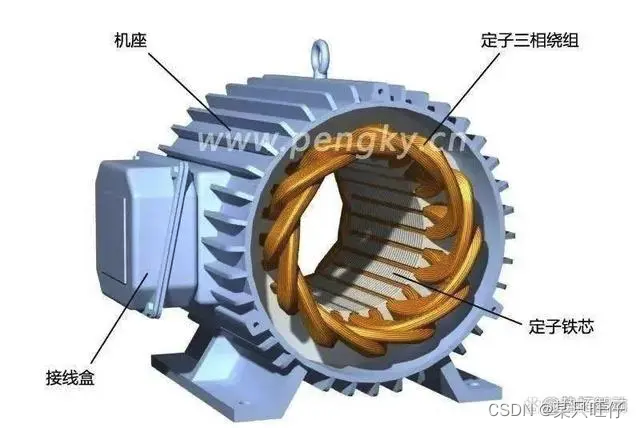
        其中第一张图为永磁同步电机的剖视图，第二张为定子结构图，第三张为转子结构图，其中转子由永磁体构成。

        在定子中通入三相交流电，每一相均在周围形成磁场，将a,b,c三相构成的磁场进行矢量合成，理论上可以得到圆形旋转磁场，我们可以将其想象成一个具有NS极的磁铁在转动。由于转子由永磁体构成，我们也可以将其看成具有NS极的磁铁。于是由于同性相斥，异性相吸，旋转磁铁转动吸引着转子也进行旋转，从而使得电能转化为机械能，实现了电动机的基本功能。

         我们将三相的相电压画在图中，形象的来看一下。其中A（）,分别为a,b,c相的基准轴，也就是说每一相对应的相电压矢量原点与基准轴原点重合，方向与其相同（值为正）或相反（值为负）。之后，我们将三个相电压进行矢量合成，可以得到合成电压。

        其中表示的是定子电压（可以使用合成电压进行等效），分别指的是定子电阻值和电流值，指的是定子磁通，求导后能得到感应电动势。由于旋转磁通产生的感应电动势远远大于定子电阻上的电压值，于是我们将定子电阻电压忽略。我们将旋转磁通写成幅值加相角的形式，并关于时间求导，得到最终结果，可以看出定子电压是超前于磁通90°，幅值不变的向量，如下面的左图所示。

         我们将左图中的电压矢量的原点放在一起，于是构成幅值相等，角度不同的多个电压矢量图，随着转动，他们共同构成了圆形旋转电压矢量。

二、坐标变换（为后续SVPWM的内容做准备）

        转载：FOC坐标变换

        引入不同的坐标系，对交流电动机的数学模型进行化简，将某些物理量在不同的坐标系之间进行变换，即坐标变换。变换遵守的原则是：不同坐标系上的绕组产生的总磁动势不变。

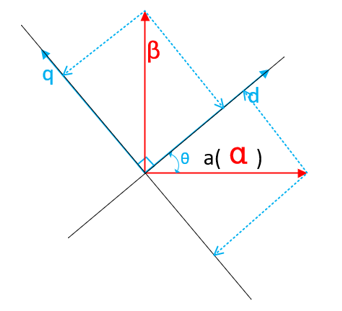
        在电机矢量控制中，主要有三相定子坐标系abc，等效的两相正交定子坐标系αβ，都是静止坐标系；还有就是两相正交转子坐标系dq，是旋转坐标系。

1. abc三相静止坐标系（3s坐标系）：

如图所示，由电机的三相绕组组成三个坐标轴，坐标轴两两相差120°，这里取a轴水平向右。

2. αβ两相静止坐标系（2s坐标系）：

如图所示，α轴和abc坐标系中的a轴重合，β轴超前α轴90°，α轴和β轴正交。

3. dq两相旋转坐标系（2r坐标系）：

如图所示，dq坐标系为转子坐标系，随着转子的转动，坐标系绕转轴转动，在转动过程中，d轴和q轴始终垂直，q轴超前d轴90°，记逆时针旋转为正方向，旋转的d轴与静止的α轴之间的夹角称为机械角度θ。

4. Clarke变换：

        由三相静止坐标系abc到两相静止坐标系αβ的变换成为Clarke变换，一般指电流变换，即ia,ib,ic变换为iα,iβ。设三相abc坐标系中每相绕组匝数为N3，等效两相αβ坐标系中每相绕组匝数为N2。

        在2s坐标系中，描述由3s坐标系绕组产生的总磁动势为：

        在2s坐标系中，描述由2s坐标系绕组产生的总磁动势为：

        由于在不同坐标系绕组产生的总磁动势相等，即

        可以得到：

        通常取匝数比 N3/N2=2/3，这样可以推出三相电流ia,ib,ic和两相电流iα，iβ的幅值是相等的（也可以取其他的匝数比，得到其他的变换系数，这里只是方便计算）。即三相坐标系绕组产生的磁动势在α和β轴的分量与α和β轴本身产生的磁动势相等。即：

        即有Clarke变换矩阵：

        在永磁同步电机模型中，有三相电流的矢量和为零，即

        故在程序中计算时，为减小计算复杂度，有：

        在实际的算法应用中，由测量得到实际的三相电流ia,ib,ic。通过Clarke变换得到等效的电流iα，iβ。

5. Clarke逆变换（IClarke）：

        由两相静止坐标系αβ到三相静止坐标系abc的变换成为Clarke逆变换，一般是指电压变换。由Clarke变换的推到关系式易得：

        在实际应用中一般为电压变换，所以常用变换矩阵为：

        由等效的期望输出电压Uα和Uβ，通过Clarke逆变换，计算得到实际的三相输出电压Ua,Ub,Uc，最后通过SVPWM计算三相电压的作用时间计算H桥开关管的通断顺序和占空比。

6. Park变换：

        由两相静止坐标系αβ到两相旋转坐标系dq的变换成为park变换，一般指电流变换，即iα，iβ变换为id,iq。变换遵守的原则同样是，不同坐标系上的绕组产生的总磁动势不变。

        等效两相αβ坐标系中每相绕组匝数为N2，dq两相坐标系中每相绕组匝数也为N2(dq坐标系相当于是由αβ坐标系旋转一个θ角度来的)。

        在2r坐标系中建立关系式，即把αβ轴的磁动势分解到dq轴。

        在2r坐标系中，描述由2s坐标系绕组产生的总磁动势为：

        在2r坐标系中，描述由2r坐标系绕组产生的总磁动势为：

        由于在不同坐标系绕组产生的总磁动势相等，即

        可得

        即αβ坐标系绕组产生的磁动势在d和q轴的分量与d和q轴本身产生的磁动势相等。即有：

        即有park变换矩阵:

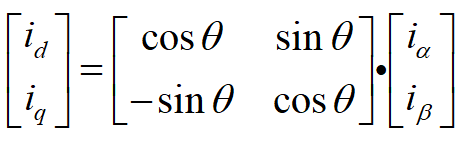
        由上一步计算得到的电流iα，iβ，和测量得到的机械角θ（机械角θ也可以由观测器估算得到），通过park变换得到等效的旋转坐标系中的电流iq,id。

        速度环根据当前速度和期望速度，输出一个期望电流iq*；q轴电流环根据当前电流iq和期望电流iq*，计算输出一个期望电压Uq；d轴电流环根据当前电流id和期望电流id*（id*一般给定为0）输出一个期望电压Ud，然后进行逆变换计算输出电压。

7. Park逆变换（IPark）：

        由两相旋转坐标系dq到两相静止坐标系αβ的变换成为park逆变换，一般指电压变换

        在2s坐标系中建立关系式，即把dq轴的磁动势分解到αβ轴。

        在2s坐标系中，描述由2s坐标系绕组产生的总磁动势为：

        在2s坐标系中，描述由2r坐标系绕组产生的总磁动势为：

        由于在不同坐标系绕组产生的总磁动势相等，即

        可得:

        即dq坐标系绕组产生的磁动势在α和β轴的分量与α和β轴本身产生的磁动势相等。即有：

        即有park逆变换矩阵

        在FOC应用中一般是电压变换，故常用

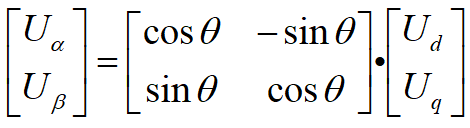
        由PI闭环控制器（一般为一个速度环和两个电流环）计算输出的Ud,Uq，通过park逆变换，得到等效的期望输出电压Uα和Uβ。

后续还会写关于SVPWM算法的理论知识....