资源限制:
内存限制:256.0MB C/C++时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s
问题描述:
任何一个正整数都可以用2的幂次方表示。例如:
137=27+23+20
同时约定方次用括号来表示,即ab 可表示为a(b)。
由此可知,137可表示为:
2(7)+2(3)+2(0)
进一步:7= 22+2+20 (21用2表示)
3=2+20
所以最后137可表示为:
2(2(2)+2+2(0))+2(2+2(0))+2(0)
又如:
1315=210 +28 +25 +2+1
所以1315最后可表示为:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
输入格式:
输入包含一个正整数N(N<=20000),为要求分解的整数。
输出格式:
程序输出包含一行字符串,为符合约定的n的0,2表示(在表示中不能有空格)
思路:
将可能的2的次方列出来,可以知道最大到2的14次方,将这些数存放到数组中,
n=1和n=2时是特殊情况,单独进行判断,其余情况用while循环遍历。
代码如下:
import java.util.*;
public class Main
{
//数组存放2的几次方
public static int [] arr=new int[] {1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384};
public static void mf(int n) {
//n=1时输出2(0)
if (n==1) {
System.out.print("2(0)");
return;
}
//n=2时输出2
if (n==2) {
System.out.print("2");
return;
}
int i=14;int j=n;
//不超过n的最大次幂
while (i>=1) {
if (j-arr[i]>=1) {
System.out.print(2);
if (i>1) {
System.out.print("(");
mf(i);
System.out.print(")");
}
j=j-arr[i];
if(j!=0)System.out.print("+");
mf(j);
return;
}
i--;
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
mf(n);
}
}
运行结果如下:
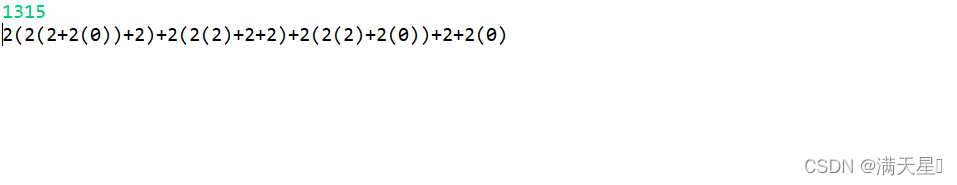










 该博客介绍了一种将任意正整数表示为2的幂次方组合的方法。通过递归算法,程序能够将输入的整数分解为不重复的2的次幂形式,输出结果中每个2的幂次方用括号括起并连接。博客内容涉及到计算机科学中的算法设计和数值表示,适合对算法和数学感兴趣的人群阅读。
该博客介绍了一种将任意正整数表示为2的幂次方组合的方法。通过递归算法,程序能够将输入的整数分解为不重复的2的次幂形式,输出结果中每个2的幂次方用括号括起并连接。博客内容涉及到计算机科学中的算法设计和数值表示,适合对算法和数学感兴趣的人群阅读。
















 306
306

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








