菊厂20250416软件机考T2解答（200分）-CSDN博客

本文链接：https://blog.csdn.net/qq_54708219/article/details/147286757

题目

已知某市运营了N条地铁线路，市民在乘坐地铁时单条线路通票2元，换乘一次加1元。给出N条线路的所有站名列表，请帮乘客寻找从出发站到目的站最便宜的地铁换乘方案，并输出票价。每条地铁线路不包含环路，即没有相同站名。

输入：

第一行为地铁线路条数N，范围是[1, 1000]

第二行到第N+1行，每条线路依次包含的站名，每个站名包含的字符个数不超过100，站点个数也不超过100，依次用空格隔开，不同线路中相同的站点名表示是一个换乘站

第N+2行，出发站和目的站，用空格隔开

输入保证：若可达则为唯一解

输出：

第一行按出发站-换乘站（可以是多个）-目的站的格式输出换乘方案的字符串

第二行输出换乘方案的总票价

如果没有任何方案实现出发站到目的站，只输出一行：NA

样例：

输入：

3
A B C D F
C E G H 
B G I J
A J

输出：

A-B-J
3

解释：

一号线有A,B,C,D,F五个站点，二号线有C,E,G,H四个站点，三号线有B,G,I,J四个站点。从A站到J站的最省钱换乘路线是经B站换乘，票价3元

代码

思路：注意本题目的地铁计费方式是按乘坐的线路条数计费的，票价 = 乘坐的地铁线路条数 + 1.所以这道题目构建图的时候应该以线路为节点去构建。

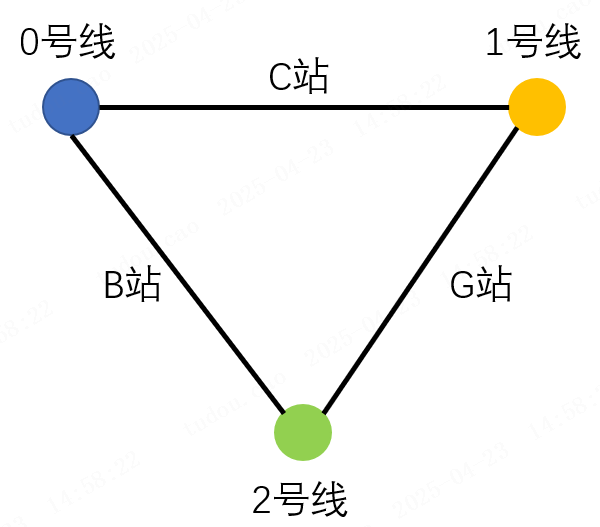
如图，根据起始和结束站点首先确定出来起始站，终点站的线路，然后以线路为节点去构建图，连接路径为换乘站，这里我用的是用邻接表去构建。

流程：

输入处理——站点与线路建立映射——直接到达检查——邻接表构建——BFS（对线路进行广度优先遍历）——路径回溯与打印输出

（代码即提交代码，注释为考后复盘所写）

from collections import defaultdict, deque
# If you need to import additional packages or classes, please import here.

def func():
    N = int(input())
    lines = []
    for i in range(N):
        line = list(map(str, input().split()))
        lines.append(line)
    start, end = list(map(str, input().split()))
    '''
    N = 3
    lines = [['A', 'B', 'C', 'D', 'F'], ['C', 'E', 'G', 'H'], ['B', 'G', 'I', 'J']]
    start, end = 'A', 'J'
    '''
    
    # 创建一个默认值为空列表的字典，用于存储每个站点（station）对应的地铁线路（lines） 
    station_to_lines = defaultdict(list)
    # 特性：当访问字典中不存在的键（key）时，自动创建该键，并赋予一个默认值（此处为 list，即空列表）
    for line_idx, stations in enumerate(lines):
        for s in stations:
            station_to_lines[s].append(line_idx)
    # station_to_lines: defaultdict(<class 'list'>, {'A': [0], 'B': [0, 2], 'C': [0, 1], 'D': [0], 'F': [0], 'E': [1], 'G': [1, 2], 'H': [1], 'I': [2], 'J': [2]})
    
    # 判断一下，起始点跟结束点是不是在同一条线路上，如果是，直接输出2，表示不用换乘，票价2元
    found_direct = False
    for line_idx in station_to_lines[start]:
    # station_to_lines[start]: [0]，起始站有可能是换乘站，需遍历所有线路
        if end in lines[line_idx]:
            print(f"{start}-{end}")
            print(2)
            exit()
    
    # 构建邻接表，记录一条线路上和其他线路的换乘站点
    adj_with_s = defaultdict(list)
    for s in station_to_lines:
        line_list = station_to_lines[s]
        for i in range(len(line_list)):
            for j in range(i + 1, len(line_list)):
                l1 = line_list[i]
                l2 = line_list[j]
                adj_with_s[l1].append((l2, s))
                adj_with_s[l2].append((l1, s))
    # adj_with_s: defaultdict(<class 'list'>, {0: [(2, 'B'), (1, 'C')], 2: [(0, 'B'), (1, 'G')], 1: [(0, 'C'), (2, 'G')]})
    
    # BFS初始化
    start_lines = station_to_lines[start]
    # start_lines: [0]，起始站经过的地铁线路列表
    end_lines = set(station_to_lines[end])
    # end_lines: {2}，终点站经过的地铁线路列表，转换为字典
    # dist数组用来记录从起始线路到各条线路的最短距离，初始化为-1表示尚未访问
    # 在题设计费方式下，不可能踏入同一条线路两次
    dist = [-1] * N
    # prev记录路径来源
    prev = {}
    # 辅助队列q
    q = deque()
    
    # 经过起始站的所有线路距离为0，标记为已访问过，并入队
    for line in start_lines:
        dist[line] = 0
        q.append(line)
        
    target_line = -1
    found = False
   
    while q:  # 当队列不为空时
        # 队头弹出节点
        current_line = q.popleft()
        # 如果弹出的线路经过终点，则结束
        if current_line in end_lines:
            target_line = current_line
            found = True
            break
        # 遍历当前线路的相邻线路（换乘线路）
        for neighbor_line, s in adj_with_s.get(current_line, []):
            # 更新最短换乘次数
            # get输出[(2, 'B'), (1, 'C')]，0号线地铁可在B站换乘2号线，在C站换乘1号线
            if dist[neighbor_line] == -1 or dist[current_line] + 1 < dist[neighbor_line]:
                # 若换乘线路未被访问过，或当前线路换乘过去的代价小于目前到达该线路的代价，则更新
                dist[neighbor_line] = dist[current_line] + 1
                prev[neighbor_line] = (current_line, s)  # 记录前驱线路和换乘站点
                q.append(neighbor_line)  # 相邻换乘线路进队，执行下一层BFS

    # dist = [0, 1, 1]，说明从B站出发，到达0号线不需要换乘，到达1号线和2号线均需要换乘1次
    # prev = {2: (0, 'B'), 1: (0, 'C')}，说明到达2号线需通过B站从0号线换乘过来，到达1号线需通过C站从0号线换乘过来 
    
    if not found:
        # 没找着，返回false
        print("NA")
        exit()
    else:
        # 找着了，开始回溯路径
        # path记录中间换乘站点
        path = []
        current_line = target_line
        # 在记录前驱换乘的prev里面找下去
        while current_line in prev:
            current_line, s = prev[current_line]
            path.append(s)
        # 这是逆序的，所以还得翻转一下
        path.reverse()
        # 然后按题设要求打印输出就行了
        res_path = start
        for i in range(len(path)):
            res_path = res_path + '-' + path[i]
        res_path = res_path + '-' + end
        print(res_path)
        k = len(path)
        cost = k + 2
        print(cost)
    # please define the python3 input here. For example: a,b = map(int, input().strip().split())
    # please finish the function body here.
    # please define the python3 output here. For example: print().

if __name__ == "__main__":
    func()

知识点

（1）defaultdict(list)

defaultdict 是什么？
- 来自 collections 模块，是 Python 内置字典（dict）的增强版。
- 特性：当访问字典中不存在的键（key）时，自动创建该键，并赋予一个默认值（此处为 list，即空列表）。
list 的作用：定义字典的默认值类型为空列表。当新键首次被访问时，会自动初始化一个空列表作为值（value）。
适用场景
- 需要将数据按键分组存储为列表时，避免手动检查键是否存在。
- 例如：统计每个站点所属的地铁线路（一个站点可能属于多个线路）。

若用普通字典实现相同功能，需手动检查键是否存在，defaultdict(list) 简化了这一过程，代码更简洁高效：

station_to_lines = {}

for station, line in stations_info:
    if station not in station_to_lines:
        station_to_lines[station] = []  # 手动初始化空列表
    station_to_lines[station].append(line)

其他常用值：