数论基本问题
约数个数问题
(1+a1) * (1+a2) * (1+a3) * ……其中a1,a2,……,a3表示的是将原数分解成质数之积的指数。
题目链接
AC代码:
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
unordered_map<int, int> primes;
while (n -- )
{
int x;
cin >> x;
for (int i = 2; i <= x / i; i ++ )
while (x % i == 0)
{
x /= i;
primes[i] ++ ;
}
if (x > 1) primes[x] ++ ;
}
LL res = 1;
for (auto p : primes) res = res * (p.second + 1) % mod;
cout << res << endl;
return 0;
}
约数之和问题
(p1 ^ 0 + p1 ^ 1 + p1 ^ 2 +……+ p1 ^ a1) * …… 一直乘到(pk ^ 0 + pk ^ 1 + pk ^ 2 + pk ^ 3 + …… + pk ^ ak)
题目链接
AC代码:
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
unordered_map<int, int> primes;
while (n -- )
{
int x;
cin >> x;
for (int i = 2; i <= x / i; i ++ )
while (x % i == 0)
{
x /= i;
primes[i] ++ ;
}
if (x > 1) primes[x] ++ ;
}
LL res = 1;
for (auto p : primes)
{
LL a = p.first, b = p.second;
LL t = 1;
while (b -- ) t = (t * a + 1) % mod;
res = res * t % mod;
}
cout << res << endl;
return 0;
}
1-n中所有1-n因子的数量
1 - n 中所有因子个数是:n/1 + n/2 + n/3 + n/4 + n/5 + …… +n/n
int res=0;
for(int i=1;i<=n;i++) res+=n/i;
n!分解后某个质因子的个数
int get(int n, int p)
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
这个方法还是挺神奇的,证明的我还不会,后面会了再更新~~
欧拉函数
1-n中与n互斥的个数,设p1,p2,p3,……,pk为n的因子,所以我们直接将n - n/p1 - n/p2 - n/p3 + n / (p1*p2) + ……后面就是容斥原理,奇负偶正了。将式子整理可得
原式=n * (1 - 1/p1) * (1 - 1/p2) * …… * (1- 1 / pk) (根据容斥原理证明)
注:与次数没有关系,如果一个数被分解成2 ^ 100 * 3 ^ 100,这种情况下仍然为 N * (1-1 / 2) * (1 - 1 / 3)
公式法求欧拉函数
#include <iostream>
using namespace std;
int phi(int x)
{
int res = x;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
res = res / i * (i - 1);//注:这里一定是先除再乘,否则计算过程中可能会出现小数,而此公式计算结果一定是整数的,而且这里如果如果先乘再除的话可能会爆int,尽量先除再乘,这也是经常处理大数据常用的方法。
while (x % i == 0) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return res;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
int x;
cin >> x;
cout << phi(x) << endl;
}
return 0;
}
线性筛求欧拉函数
void get_eulers(int n)
{
euler[1] = 1;
for (int i = 2; i <= n; i ++ )
{
if (!st[i])
{
primes[cnt ++ ] = i;
euler[i] = i - 1;//如果数本来是质数,直接就是i-1。
}
for (int j = 0; primes[j] <= n / i; j ++ )
{
int t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0)
{
euler[t] = euler[i] * primes[j];//如果当前到了i的最小质因子,那么我们发现i * prime[j]实际上的含有的质因子和i是一样的,因为i与i * prime[j]都含有i含有的全部质数和prime[j]而i中含有prime[j]所以两者的欧拉函数值除了N以外是一样的,故公式就是如上
break;
}
euler[t] = euler[i] * (primes[j] - 1);//如果mod不为0的情况下,i*prime[j] 中不仅含有i中全部的质因子,还含有prime[j],所以euler[t]=euler[i]*(1-1/prime[j])*prime[j],化简可以得:euler[t]=euler[i] * (prime[j]-1),这里一定是要化简的,因为euler中的所有值都是整数。
}
}
}
欧拉函数在线性筛中的三种情况:
1:如果当前数本来是质数,直接就是euler[i] = i-1。
2:如果当前到了i的最小质因子,那么我们发现i * prime[j]实际上的含
有的质因子和i是一样的,因为i与i * prime[j]都含有i含有的全部质数和prime[j]而i中含有prime[j]所以两者的欧拉函数值除了N以外是一样的,故公式就是如上
3:如果mod不为0的情况下,i * prime[j] 中不仅含有i中全部的质因子,还含有prime[j] 所以euler[t]=euler[i] * (1 - 1 / prime[j]) * prime[j] ,化简可以得:euler[t]=euler[i] * (prime[j]-1),这里一定是要化简的,因为euler中的所有值都是整数。
欧拉定理
如果a与n互质,那么a ^ (f(n)) mod n = 1 ,那么a * a(f(n)-1) mod n = 1, 我们这里可以看到 a^(f(n)-1) 即为a的逆元,所以欧拉函数可以用来求逆元(这里要求是a与n是互质的)
逆元
费马定理求逆元
费马定理:费马定理是欧拉定理的一种特殊情况,如果a,p互质且p为质数,那么f§ = p-1,即a ^ (p-1) mod p = 1,我们把a提取出来,则a * a ^ (p-2) mod p =1,a ^ (p-2) 即为a在模p下的逆元。
费马小定理:除以一个数等于乘以这个数的逆元: a p − 1 a^{p-1} ap−1 ≡ \equiv ≡ 1(mod p),(a,p互质),我们发现 a p − 2 a^{p-2} ap−2相当于1/a在mod p操作下。
费马大定理:
x
n
+
y
n
=
z
n
x^{n}+y^{n}=z^{n}
xn+yn=zn在n>2的时候没有正整数解,下面我们分类:
n=0:x=0,y=0,z=0是解
n=1:x+y=z,很多解
n=2:勾股数
n>2:无正整数解
构造勾股数:
(1)
2
n
+
1
2n+1
2n+1、
2
n
2
+
2
n
2n^{2}+2n
2n2+2n、
2
n
2
+
2
n
+
1
2n^{2}+2n+1
2n2+2n+1(n为正整数)是一组勾股数。
(2)
2
(
n
+
1
)
2(n+1)
2(n+1)、
n
2
+
2
n
n^{2}+2n
n2+2n、
n
2
+
2
n
+
2
n^{2}+2n+2
n2+2n+2(n为正整数)是一组勾股数。
(3)
m
2
−
n
2
m^{2}-n^{2}
m2−n2、2mn、
m
2
+
n
2
m^{2}+n^{2}
m2+n2(m、n表示两个不同的正整数且m>n)是一组勾股数。
(4)如果a、b、c是一组勾股数那么na、nb、nc(n为正整数)也是一组勾股数。
快速幂求逆元
按照费马定理,假设mod和a互质,qmi(a,mod,mod-2)求出来的即为a在mod下的逆元,这样的话我们只需要一个快速幂和模就可以求出逆元了。
我们在这里再简单的介绍一下裴蜀定理
裴蜀定理:对于任意正整数a,b,一定存在非零整数x,y,使得ax+by=k*gcd(a,b),(k!=0)
扩展欧几里得算法
扩展欧几里得算法证明
gcd(a,b)=gcd(b,a%b),其实也是gcd(a%b,b)但是在具体的代码实现中。我们保证第二个数是小数,这样到了最后答案直接是第一个, 操做起来比较方便。下面证明exgcd:
ax + by = gcd(a,b),可以同理得到by+(a%b)x=gcd(a,b),这样依次循环下去,化简:by+(a - a/b * b) * x = gcd(a,b),即ax + b *(y - a/b * x)=gcd(a,b)。
假设开始的时候是aX0+bY0=gcd(a,b)
然后递归迭代一次是bX1+(a%b)Y1=gcd(b,a%b)
然而gcd(b,a%b)=gcd(a,b)
a * X0+b * Y0=b * X1+(a%b) * Y1
a * X0+b * Y0=b * X1+(a - a / b * b ) * Y1
a * X0+b * Y0=b * X1+a * Y1-a / b * b * Y1
a * X0+b * Y0=a * Y1 + b * (X1 - a / b * b * Y1)
分析可得:X0=Y1,Y0=X1 - a / b * b * Y1
我们分析公式可得,每一次迭代,X和Y都是交叉相联系的,所以如果我们在进行下一步递归时,在递归式里将X,Y进行交换这样就可以简化操作原来等式就变成:X0=X1,Y0=Y1 - (a / b * b * X1),这样在进行操作的时候就可以直接在当前的递归层数不对X进行操作,仅仅对进行操作即可。
下面时模板代码:
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);//这里x,y交换位置方便操作
y -= a / b * x;
return d;
}
当然,我们在得到一组特解之后就可以得到所有的解:
由题可得:
aX0+bY0=gcd(a , b),我们假设X’,Y’为通解
aX’+bY’ = gcd(a , b)
X’=X0 + b/gcd(a , b) * k
Y’=Y0 - a/gcd(a , b) * k
X’最小的非负整数解:
(X0 % (b / gcd(a,b) ) + b / gcd(a , b) ) % (b / gcd(a,b) )
下面可以简单证明一下:就是X0 % (b / gcd(a ,b)) = X0 - X0 / (b / gcd(a , b) ) * (b / gcd(a,b) ) ,这是在与x同号的情况下离0最近的答案,如果再加上b / (gcd(a, b) )一定是大于0的且是最小的。
扩展欧几里得的应用
1:求线性同余方程
ax=c(%p) 这里可以改写为ax + py = c 其中的几个值,也就可以求出想要的值
2:求逆元
3:同上解不定方程
中国剩余定理
设
m
1
,
m
2
,
m
3
,
…
…
,
m
k
m_{1},m_{2},m_{3},……,m_{k}
m1,m2,m3,……,mk两两互质,则同余方程组:
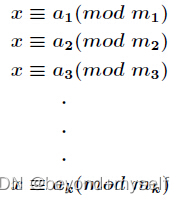
我们令M=
m
1
∗
m
2
∗
m
3
∗
…
…
m
k
m_{1}*m_{2}*m_{3}*……m_{k}
m1∗m2∗m3∗……mk
我们令
M
i
=
M
/
m
i
M_{i}=M/m_{i}
Mi=M/mi,
M
i
−
1
M_{i}^{-1}
Mi−1表示
M
i
M_{i}
Mi的mod
m
i
m_{i}
mi的逆元
则
x
=
a
1
∗
M
1
∗
M
1
−
1
+
a
2
∗
M
2
∗
M
2
−
1
+
a
3
∗
M
3
∗
M
3
−
1
∗
…
…
∗
a
k
∗
M
k
∗
M
k
−
1
x=a_{1}*M_{1}*M_{1} ^ {-1}+a_{2}*M_{2}*M_{2} ^ {-1}+a_{3}*M_{3}*M_{3} ^ {-1}*……*a_{k}*M_{k}*M_{k}^{-1}
x=a1∗M1∗M1−1+a2∗M2∗M2−1+a3∗M3∗M3−1∗……∗ak∗Mk∗Mk−1
我们可以证明一下这个解的正确性:
x%m1的时候除了第一项不含
m
1
m_{1}
m1其余项中均含
m
1
m_{1}
m1所以,其余项模
m
1
m_{1}
m1后均为0,而此项
x
=
a
1
∗
M
1
∗
M
1
−
1
x=a_{1}*M_{1}*M_{1} ^ {-1}
x=a1∗M1∗M1−1
M
1
M_{1}
M1与
M
1
−
1
M_{1}^{-1}
M1−1在模
m
1
m_{1}
m1下互为逆元,所以为1,所以
x
x
x与
a
1
a_{1}
a1在mod
m
1
m_{1}
m1下相同,其余项证明同理。
这个详细的不再证明,另外好像还有中国剩余定理的扩展,这里不再介绍,放上一道例题:戳一戳
高斯消元
高斯消元简介
简介:简单来说,高斯消元就是线代中的求解线性方程组过程,其时间复杂度大概在O(n^3)左右

以上是原始的方程组,我们通常写成增广矩阵形式
(
a
11
a
12
…
a
1
n
a
21
a
22
…
a
2
n
…
…
…
…
a
n
1
a
n
2
…
a
n
n
)
(2)
\left( \begin{matrix} a_{11} & a_{12} & … & a_{1n}\\ a_{21} & a_{22} & … & a_{2n} \\ … &… & … & …\\ a_{n1}&a_{n2}&… & a_{nn} \end{matrix} \right) \tag{2}
⎝⎜⎜⎛a11a21…an1a12a22…an2…………a1na2n…ann⎠⎟⎟⎞(2)
前置知识:初等行(列)变换
1:对某一行乘以一个非零的数
2:交换某两行
3:把某行的若干倍加到令一行上去
通过以上的变换,将增广矩阵转换成一个阶梯矩阵:
(
a
b
⋯
a
0
b
⋯
b
⋮
⋮
⋱
⋮
0
0
⋯
c
)
(5)
\left( \begin{matrix} a & b & \cdots & a\\ 0 & b & \cdots & b\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & c \end{matrix} \right) \tag{5}
⎝⎜⎜⎜⎛a0⋮0bb⋮0⋯⋯⋱⋯ab⋮c⎠⎟⎟⎟⎞(5)
类似于以上的一个上三角矩阵,然后从下往上推就可以求出解
解的情况
方程的解有三种情况:
无解
有一个解
有无穷个解
算法的步骤
以下是算法的步骤:
1:枚举方程的每一列
2:找出这一列的绝对值的最大值的那一行放到最上面(并不是整体的第一行而是未确定的第一行)
3:将该行的第一个非零元素转化成1
4:用初等行变换将该行一下所有的该列数变换成0(逐步形成上三角的过程)
算法的实现
对应例题:戳一戳
下面是相应代码:
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const double eps=1e-8;//double类型,所以可能很难有绝对的0和相等,我们就是设值一个值,小于某个值就假设这两个数相等或这个数是0
int n;
double a[N][N];
int gauss()
{
int c,r;
for(c=0,r=0;c<n;c++)
{
int t=r;//r指当前的行,c指当前的列
for(int i=r;i<n;i++)//找该列绝对值最大的元素的所在的行
if(fabs(a[i][c])>fabs(a[t][c]))
t=i;
if(fabs(a[t][c])<eps) continue;//如果这一行最大值是0了,那么所有的值都是0,不必在转换
for(int i=c;i<=n;i++)//交换两行元素
swap(a[t][i],a[r][i]);
for(int i=n;i>=c;i--) a[r][i]/=a[r][c];//将当前行的首元素转化为1,尽量倒着往前,不然还得需要记录一下第一个值
for(int i=r+1;i<=n;i++)
if(fabs(a[i][c])>eps)
for(int j=n;j>=c;j--)//将该行下面的所有行的第一个元素变为0
a[i][j]-=a[r][j]*a[i][c];
r++;//r只有不被continue时才会到下一行,因为我们每一行都要将第一个非0的数转化为1才行
}
if(r<n)//也就是r后面的数应该都是0才对
{
for(int i=r;i<=n;i++)
{
if(fabs(a[i][n])>eps)//假设r下面的行非0,实际上是无解的,因为我们按照此规则得到的矩阵式r行即下面的矩阵全部是0的,可以自己举个例子看一看
return 2;
}
return 1;
}
for(int i=n-1;i>=0;i--)
for(int j=i+1;j<n;j++)
a[i][n]-=a[j][n]*a[i][j];//很妙,因为我们是从下往上的,所以当我们枚举到当前值的时候,后面的值都能够得到了,所以我们通过在每一行将去要求的值那一列后面所有的求出来的值,就只剩下了答案
return 0;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<=n;j++)
scanf("%lf",&a[i][j]);
int t=gauss();
if(t==0)
{
for (int i = 0; i < n; i ++ )
{
if (fabs(a[i][n]) < eps) a[i][n] = 0; // 去掉输出 -0.00 的情况
printf("%.2lf\n", a[i][n]);
}
}
else if(t==1) printf("Infinite group solutions\n");
else printf("No solution\n");
return 0;
}
组合数学(组合数求法)
杨辉三角求组合数
时间复杂度O(n ^ 2)
对应例题:戳一戳
对应模板:
void init()
{
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
通过公式来求
时间复杂度:O(nlogn)
公式:
C
n
m
=
n
!
m
!
(
n
−
m
)
!
C_{n} ^ {m}=\frac{n!}{m!(n-m)!}
Cnm=m!(n−m)!n!
模板:
infact[x]表示x的阶乘的逆元
fact[x]表示x的阶乘
int a,b;
cin>>a>>b;
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
卢卡斯定理
使用范围:1<=n<=m<=1e18(大致,应该还可以更大点)
C
n
m
=
C
n
%
p
m
%
p
∗
C
n
/
p
m
/
p
(
%
p
)
C_{n} ^ {m}=C_{n\%p} ^ {m\%p}*C_{n/p} ^ {m/p}(\%p)
Cnm=Cn%pm%p∗Cn/pm/p(%p)
对应例题:戳一戳
模板:
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
int res = 1;
for (int i = 1, j = a; i <= b; i ++, j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
总共有三部分:求组合数,快速幂,卢卡斯的递归
通过质因数分解来求
时间复杂度:O(n^2)
对应例题:戳一戳
公式:
C
n
m
=
n
!
m
!
(
n
−
m
)
!
=
p
1
a
1
∗
p
2
a
2
∗
…
∗
p
n
a
n
C_{n} ^ {m}=\frac{n!}{m!(n-m)!}=p1^{a1}*p2^{a2}*…*pn^{an}
Cnm=m!(n−m)!n!=p1a1∗p2a2∗…∗pnan
我们可以求出n!可以分解的质因数,m!分解的质因数,(n-m)!的所有质因数,所以我们将所有的因数找出来后就直接乘法计算就可以了,上述原题会用到高精度,至于那个n!分解后的的某个质因数的个数,上面已经讲过了,这里直接看代码:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N], cnt;
int sum[N];
bool st[N];
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n, int p)
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
int main()
{
int a, b;
cin >> a >> b;
get_primes(a);
for (int i = 0; i < cnt; i ++ )
{
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p);//这里是那个公式,我们要记得减去(a-b)!和那个b!中的因子数
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);//这里用到了高精度
for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
puts("");
return 0;
}
卡特兰数
先找一个例题来求卡特兰数:

提交:戳一戳
首先任意前缀序列中的0的个数都不少于1的个数,我们可以将其放到二维平面中去左,0表示左移,1表示上移,这样的就是可以得出下面的图,根据线性规划
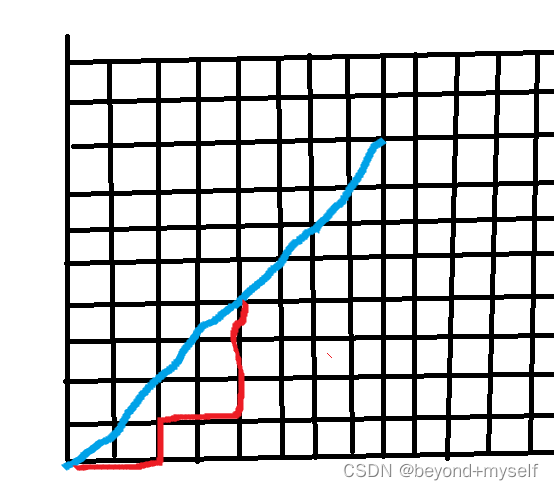
我们发现,只要是在蓝线的下面走就可以保证0的个数一定是大于等于1的个数
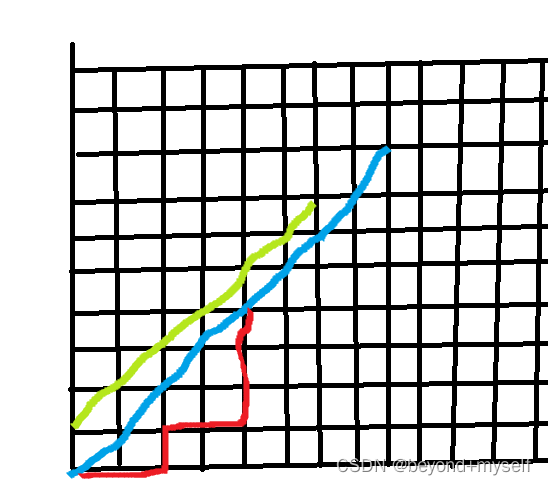
但是只要是经过了那个绿色的线,就无法满足情况了。
假设我们走到了(4,4)这个格子,那么所有的情况就是
C
8
4
C_{8}^{4}
C84

我们又发现,每一个经过黄线到达蓝线的红线最终到达(4,4)这个点都有一条线与黄线对称到达(3,5)这条线,这样答案就出来了:
C
8
4
−
C
8
3
C_{8}^{4}-C_{8}^{3}
C84−C83,这样我们可以发现,到达任意一点的方案数就是
C
2
n
n
−
C
2
n
n
−
1
C_{2n}^{n}-C_{2n}^{n-1}
C2nn−C2nn−1中情况,我们化简一下就是
C
2
n
n
/
(
n
+
1
)
C_{2n}^{n}/(n+1)
C2nn/(n+1)这就是卡特兰数,很多例子都是卡特兰数,有兴趣的可以到网上搜一下
这样的话题目就很简单了:
下面是参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200010, mod = 1e9 + 7;
int n;
int fact[N], infact[N];
int ksm(int a, int k) {
int res = 1;
while (k) {
if (k & 1) res = (LL)res * a % mod;
a = (LL)a * a % mod;
k >>= 1;
}
return res;
}
void init() {
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i++) {
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * ksm(i, mod - 2) % mod;
}
}
int main() {
init();
cin >> n;
int res = (LL)fact[2 * n] * infact[n] % mod * infact[n] % mod * ksm(n + 1, mod - 2) % mod;
cout << res << endl;
return 0;
}






















 206
206











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








