算法分析之递归

一、什么是递归

1、定义

①递归：在定义一个过程或函数时出现调用本过程或本函数的成分。
②直接递归：调用自身。
③间接递归：过程或函数p调用过程或函数q，而q又调用p。
④任何间接递归都可以等价地转换为直接递归。
⑤尾递归：一个递归过程或递归函数中递归调用语句是最后一条执行语句。

2、什么时候使用递归

• 【定义是递归的】

部分数学公式或数列等的定义，如求n！或Fibonacci数列等。

• 【数据结构是递归的】

//单链表结构
//求一个不带头结点的单链表L的所有data域（假设为int型）之和
int Sum(LinkList *L)
{ if (L==NULL)
return 0;
else
return(L->data+Sum(L->next));
}

//二叉树的二叉链存储结构
//求非空二叉链bt中所有结点值之和的递归算法，假设二叉链的data域为int型。

//二叉树采用二叉链存储结构，其结点类型定义如下：
typedef struct BNode
{ 	int data;
	struct BNode *lchild，*rchild;
} BTNode; //二叉链结点类型

//算法如下：
int Sumbt(BTNode *bt) //求二叉树bt中所有结点值之和
{ 	if (bt->lchild==NULL && bt->rchild==NULL)
		return bt->data; //只有一个结点时返回该结点值
	else //否则返回左、右子树结点值之和加上根结点值
		return Sumbt(bt->lchild)+ Sumbt(bt->rchild)+bt->data);
}

• 【问题的求解方法是递归的】

Hanoi问题（汉诺塔问题）

//设Hanoi(n，x，y，z)表示将n个盘片从x通过y移动到z上
Hanoi(n-1，x，z，y)；
move(n，x，z):将第n个圆盘从x移到z；
Hanoi(n-1，y，x，z)

3、递归模型

递归模型=递归出口+递归体

①对原问题f(Sn)进行分析，抽象出合理的“子问题” f(sSn-1)
②假设f(Sn-1)是可解的，在此基础上确定f(Sn)的解，即给出f(Sn)与f(Sn-1)之间的关系
③确定一个特定情况（如f(1)或f(0)）的解，由此作为递归出口
【其中n、n-1为S的下标】

4、递归的执行过程

①每次调用相同函数，但它的参数、输入数据等均有变化，保证其各个调用的独立性
②调用栈：
想象我们向一个桶中（桶的直径略大于圆盘，桶底部封口）依次放入圆盘，假设我想知道桶有多深，那我们先将a放入最底部，发现还有空间，于是依次放入b、c、d、e，发现桶满，但我忘了已经放了多少个盘子，于是只能依次拿出e、d、c、b、a，当拿到a时，我就知道桶深度为5！我们这里关注一下整个过程，分为两步，先依次放入5个盘子，然后再依次拿出5个盘子，这就是调用栈的压入和弹出！

#include <stdio.h>
void f(int n)
{ 	if (n<1) 
		return;
	else
		{	printf("调用f(%d)前，n=%d\n"，n-1，n);
			f(n-1);
			printf("调用f(%d)后:n=%d\n"，n-1，n);
		}
}
//执行结果
调用f(3)前，n=4
调用f(2)前，n=3
调用f(1)前，n=2
调用f(0)前，n=1
调用f(0)后: n=1
调用f(1)后: n=2
调用f(2)后: n=3
调用f(3)后: n=4

二、递归的算法设计

1、一般步骤

先给出递归模型，再转换成对应的C/C++语言函数

• 【例题】
  用递归法求一个整数数组a的最大元素

• 【分析】

①设f(a,i)求解数组a中前i个元素即a[0…i-1]中的最大元素，则f(a,i-1)求解数组a中前i-1个元素即a[0…i-2]中的最大元素。
②假设f(a,i-1)已求出，则有f(a,i)=MAX{f(a,i-1)，a[i-1]}。递推方向是朝a中元素减少的方向推进，当a中只有一个元素时，该元素就是最大元素，所以f(a,1)=a[0]

• 【递归模型】

当i=1时，f(a,i)=a[0]
当i>1时，f(a,i)=MAX{f(a,i-1),a[i-1]}

• 【算法实现】

int fmax(int a[],int i)
{ 
	if (i==1)
		return a[0];
	else
		return(fmax(a，i-1),a[i-1]);
}

2、递归数据结构及其算法设计

①定义

采用递归方式定义的数据结构称为递归数据结构。在递归数据结构定义中包含的递归运算称为基本递归运算。

递归数据结构用数学符号表示：
RD=(D,Op)
其中，D={di}（i为下标，1≤i≤n，共n个元素）为构成该数据结构的所有元素的集合。
Op是基本递归运算的集合，Op={opj}（j为下标，1≤j≤m，共m个基本递归运算），对于任意di∈D，不妨设opj为一元运算符，则有opj(di)∈D，也就是说，递归运算符具有封闭性

②递归算法设计

【单链表】

• 【例题】
  有一个不带头结点的单链表L，设计一个算法释放其中所有结点
• 【分析】

①设L={a1，a2，…，an}，f(L)的功能是释放a1～an的所有结点，则f(L->next)的功能是释放a2～an的所有结点。
②假设f(L->next)是已实现，则f(L)就可以采用先调用f(L->next)，然后释放L所指结点来求解

• 【递归模型】

当L=NULL时， f(L) ≡不做任何事件
else，f(L) ≡ f(L->next); 释放*L结点

• 【算法实现】

void DestroyList(LinkNode *&L)   //释放单链表L中所有结点
{ 
	if (L!=NULL)
	{ 
		DestroyList(L->next);
		free(L);
	}
}

【二叉树】

• 【例1】
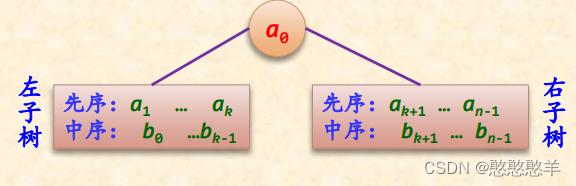
  对于含 n（n>0）个结点的二叉树，所有结点值为int类型，设计一个算法由其先序序列a和中序序列b创建对应的二叉链存储结构
• 【分析】

先序序列：

中序序列：
得出：

• 【算法实现】

BTNode *CreateBTree(ElemType a[],ElemType b[],int n)     //由先序序列a[0..n-1]和中序序列b[0..n-1]建立二叉链存储结构bt
{ 
	int k;
	if (n<=0) return NULL;
	ElemType root=a[0]; //根结点值
	BTNode *bt=(BTNode *)malloc(sizeof(BTNode));
	bt->data=root;
	for (k=0;k<n;k++) //在b中查找b[k]=root的根结点
		if (b[k]==root)
			break;
			
	bt->lchild=CreateBTree(a+1,b,k); //递归创建左子树
	bt->rchild=CreateBTree(a+k+1,b+k+1,n-k-1); //递归创建右子树
	
	return bt;
}

• 【例2】
  设计一个递归算法，输出一个大于零的十进制数n的各数字位，如n=123，输出各数字位为123
• 【分析】

设n为m位十进制数a m-1 a m-2…a1a0（m>0），则有:
n%10=a0，n/10=a m-1 a m-2…a1。
设f(n)的功能是输出十进制数n的各数字位，则f(n/10)的功能是输出除a0（即n%10）外的各数字位

• 【递归模型】

当n＝0，f(n) ≡不做任何事件
else，f(n)≡ f(n/10); 输出n％10

• 【算法实现】

void digits(int n)
{ 
	if (n!=0)
	{ 
		digits(n/10);
		printf("%d"，n%10);
	}
}

三、示例

1、简单选择排序

• 【问题】
  对于给定的含有n个元素的数组a，用简单选择排序对其按元素值递增排序
• 【分析】
• 【递归模型】
• 【算法实现】

2、冒泡排序

• 【问题】
  对于给定的含有n个元素的数组a，用冒泡排序对其按元素值递增排序
• 【分析】

设f(a，n，i)用于对a[i…n-1]元素序列（共n-i个元素）进行冒泡排序，是“大问题”，则f(a，n，i+1)用于对a[i+1…n-1]元素序列（共n-i-1个元素）进行冒泡排序，是“小问题”。当i=n-1时所有元素有序，算法结束

• 【递归模型】

① 当i=n-1，f(a，n，i) ≡ 不做任何事情，算法结束
② else，f(a，n，i) ≡ 对a[i…n-1]元素序列，从a[n-1]开始进行相邻元素比较;
若相邻两元素反序则将两者交换;
若没有交换则返回，否则执行f(a，n，i+1);

• 【算法实现】

void BubbleSort(int a[]，int n，int i)
{ 
	int j;
	bool exchange;
	if (i==n-1) return; //满足递归出口条件
	
	else
	{ 
		exchange=false; //置exchange为false
		for (j=n-1;j>i;j--)
			if (a[j]<a[j-1]) //当相邻元素反序时
			{ 
				swap(a[j],a[j-1]);
				exchange=true; //发生交换置exchange为true
			}
		if (exchange==false) //未发生交换时直接返回
			return;
		else //发生交换时继续递归调用
			BubbleSort(a，n，i+1);
	}
}

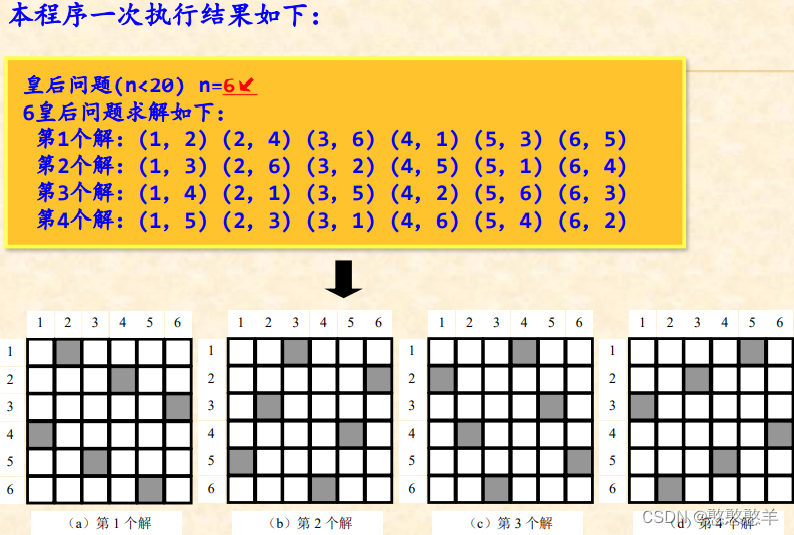
3、求解n皇后问题

• 【问题】
  在n×n的方格棋盘上，放置n个皇后，要求每个皇后不同行、不同列、不同左右对角线。如下图所示是6皇后问题的一个解

• 【分析】

① 设queen(i，n)是在1～i-1列上已经放好了i-1个皇后，用于在i～n行放置n-i+1个皇后，则queen(i+1，n)表示在1～i 行上已经放好了i个皇后，用于在i+1～n行放置n-i个皇后。
②queen(i+1，n)比queen(i，n)少放置一个皇后。所以queen(i+1，n)是“小问题”，queen(i，n)是“大问题”。

• 【递归模型】

① 若k>n，queen(i，n) ≡ n个皇后放置完毕，输出一个解
② else，queen(i，n) ≡ 在第i行的合适的位置（i,j）
在其上放置一个皇后;
queen(i+1，n);

• 【算法实现】

bool place(int i,int j) //测试(i,j)位置能否摆放皇后
{ 
	if (i==1) return true; //第一个皇后总是可以放置
	int k=1;
	while (k<i) //k=1～i-1是已放置了皇后的行
	{ 
		if ((q[k]==j) || (abs(q[k]-j)==abs(i-k)))
			return false;
		k++;
	}
	return true;
}

void queen(int i,int n) //放置1～i的皇后
{ 
	if (i>n) 
		dispasolution(n); //所有皇后放置结束
	else
	{ 
		for (int j=1;j<=n;j++) //在第i行上试探每一个列j
			if (place(i,j)) //在第i行上找到一个合适位置(i,j)
			{ 
				q[i]=j;
				queen(i+1,n);
			}
	}
}

• 【运行结果】
  

四、解释

本文相当于学习笔记，按照学校老师的ppt进行选择整理