运筹学网络模型

林深时见鹿-1

于 2022-04-20 09:28:09 发布

阅读量990

点赞数

分类专栏：数学建模文章标签： python c++ 算法图论

本文链接：https://blog.csdn.net/qq_55729911/article/details/124289519

版权

数学建模专栏收录该内容

1 篇文章 0 订阅

订阅专栏

1.最小生成树

1.1 什么是树？

如果一个无向连通图不包含回路(连通图中不存在环),那么就是一个树。
如下图所示即为一个数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pm3hK7WV-1650418044140)(C:\Users\Lin\AppData\Roaming\Typora\typora-user-images\1650351532633.png)]

1.2 什么是最小生成树

最小生成树，顾名思义，就是在某个图结构中进行选取构造，构造出一个树。一个有N个点的图，边一定是大于等于N-1条的。图的最小生成树，就是在这些边中选择N-1条出来，连接所有的N个点。这N-1条边的边权之和是所有方案中最小的。

1.3 最小生成树的构造

（1）prim算法

prim算法又称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

也就是说，每次迭代将会把图中某一点选中，确保点到已连接区域为最短距离。

代码如下（代码来源）：

/*
*邮箱：unique_powerhouse@qq.com
*blog:https://me.csdn.net/hzf0701
*注：文章若有任何问题请私信我或评论区留言，谢谢支持。
*
*/
#include<bits/stdc++.h>	//POJ不支持

#define rep(i,a,n) for (int i=a;i<=n;i++)//i为循环变量，a为初始值，n为界限值，递增
#define per(i,a,n) for (int i=a;i>=n;i--)//i为循环变量， a为初始值，n为界限值，递减。
#define pb push_back
#define IOS ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
#define fi first
#define se second
#define mp make_pair

using namespace std;

const int inf = 0x3f3f3f3f;//无穷大
const int maxn = 1e3;//最大值。
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll>  pll;
typedef pair<int, int> pii;


int n,m;//图的大小和边数。
int graph[maxn][maxn];//图
int lowcost[maxn],closest[maxn];//lowcost[i]表示i到距离集合最近的距离，closest[i]表示i与之相连边的顶点序号。
int sum;//计算最小生成树的权值总和。
void Prim(int s){
	//初始化操作，获取基本信息。
	rep(i,1,n){
		if(i==s)
			lowcost[i]=0;
		else
			lowcost[i]=graph[s][i];
		closest[i]=s;
	}
	int minn,pos;//距离集合最近的边，pos代表该点的终边下标。
	sum=0;
	rep(i,1,n){
		minn=inf;
		rep(j,1,n){
			//找出距离点集合最近的边。
			if(lowcost[j]!=0&&lowcost[j]<minn){
				minn=lowcost[j];
				pos=j;
			}
		}
		if(minn==inf)break;//说明没有找到。
		sum+=minn;//计算最小生成树的权值之和。
		lowcost[pos]=0;//加入点集合。
		rep(j,1,n){
			//由于点集合中加入了新的点，我们要去更新。
			if(lowcost[j]!=0&&graph[pos][j]<lowcost[j]){
				lowcost[j]=graph[pos][j];
				closest[j]=pos;//改变与顶点j相连的顶点序号。
			}
		}
	}
	cout<<sum<<endl;//closest数组就是我们要的最小生成树。它代表的就是边。
}
void print(int s){
	//打印最小生成树。
	int temp;
	rep(i,1,n){
		//等于s自然不算，故除去这个为n-1条边。
		if(i!=s){
			temp=closest[i];
			cout<<temp<<"->"<<i<<"边权值为："<<graph[temp][i]<<endl;
		}
	}
}
int main(){
	//freopen("in.txt", "r", stdin);//提交的时候要注释掉
	IOS;
	while(cin>>n>>m){
		memset(graph,inf,sizeof(graph));//初始化。
		int u,v,w;//临时变量。
		rep(i,1,m){
			cin>>u>>v>>w;
			//视情况而论，我这里以无向图为例。
			graph[u][v]=graph[v][u]=w;
		}
		//任取根结点，我这里默认取1.
		Prim(1);
		print(1);//打印最小生成树。
	}
	return 0;
}

算法流程：

1.初始化三大件visited数组，lowcost数组，closest，其中lowcost[i]表示i到距离集合最近的距离，closest[i]表示i与之相连边的顶点序号。visited数组可以被优化掉，因为当lowcost数组元素值为0的时候，就代表该点在生成树中。

2.首先根据起始点，将lowcost初始化为到起始点距离，closest初始化为起始点。

3.随后开始在lowcost中寻找距离生成树区域的最短距离及点，可以使用优先队列优化。

4.随后利用新的点，更新lowcost数组和closest数组。

5.随后重复3-4操作，直到所有点都被加入到生成树区域中。

（2）Kruskal算法

如果说，prim算法是插点法的话，克鲁斯卡尔就是插边法，每次在图中选择出一条最小边，并将这条边加入生成树中，如果满足树结构，就保留，否则就挑选下一个。因此克鲁斯卡尔算法中图需要使用edge边数组存储。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Au3zDMqj-1650418044142)(C:\Users\Lin\AppData\Roaming\Typora\typora-user-images\1650379029687.png)]

具体实现代码如下（代码来源）：

#include <bits/stdc++.h>

using namespace std;

const int N = 200, M = 0x7fffffff;
typedef char vextype;

typedef struct 
{
    vextype vex[N];
    int arcs[N][N];
    int vexnum, arcnum;
}AMGraph;

struct EdgeM
{
    vextype Head;
    vextype Tail;
    int lowcost;
}Edge[N];

int Vexset[N];//辅助数组，用于排除Kruskal出现环的情况
/*思路：在Vexset数组中分别查找v1和v2所在的连通分量vs1和vs2，进行判断
1. 如果vs1 != vs2 表明两个点处于不同的连通分量，输出此边，合并vs1和vs2两个连通分量
2. 如果vs1和vs2相等，表明所选两个顶点属于同一个连通分量，那么则舍去此边选择下一个权值最小的边
*/
int minspatree_matrix[N][N];//最小生成树的邻接矩阵
pair <int, int> ans[N];

void CreatGraph(AMGraph &G)
{
    cout << "请输入顶点数目和边的数目：" << endl;
    cin >> G.vexnum >> G.arcnum;
    
    for (int i = 0; i < G.vexnum; ++ i) {
        for (int j = 0; j < G.vexnum; ++ j)
            G.arcs[i][j] = M;
    }
    cout << "请输入所有顶点名称：" << endl;
    for (int i = 0; i < G.vexnum; ++ i) cin >> G.vex[i];

    cout << "请输入所有边的权值：" << endl;
    int x, y, w;
    for (int i = 0; i < G.arcnum; ++ i) {
        cin >> x >> y >> w;
        G.arcs[x][y] = G.arcs[y][x] = w;
        Edge[i] = {G.vex[x], G.vex[y], w};
    }
}
/*下面是对书中Sort函数的实现*/
bool cmp(const EdgeM &a, const EdgeM &b)
{
    return a.lowcost < b.lowcost;
}

void Sort(AMGraph G)
{
    sort(Edge, Edge + G.arcnum, cmp);
}

int Locate(AMGraph G, vextype v)
{
    for (int i = 0; i < G.arcnum; ++ i) {
        if (G.vex[i] == v) return i;
    }
    return -1;
}

void MiniSpanTree(AMGraph &G)
{
    Sort(G);
    int cnt = 0;
    for (int i = 0; i < G.vexnum; ++ i) Vexset[i] = i;//初始时，每个点为一个单独的连通分量                                                 
    for (int i = 0; i < G.arcnum; ++ i) {//*这层循环是有问题的，选边的总数为G.vexnum - 1
        int v1 = Locate(G, Edge[i].Head);//而不是遍历所有的边，但是书上面就是这么写的
        int v2 = Locate(G, Edge[i].Tail);//仅供基础学习基本思路。

        int vs1 = Vexset[v1];
        int vs2 = Vexset[v2];

        if (vs1 != vs2)
        {
            cout << Edge[i].Head << ' ' << Edge[i].Tail << endl;
            ans[cnt ++] = {Locate(G, Edge[i].Head), Locate(G, Edge[i].Tail)};//c++11标准，c99会警告，分开赋值即可
            for (int j = 0; j < G.vexnum; ++ j) {
                if (Vexset[j] == vs2) Vexset[j] = vs1;
            }
        }
    }
    // for (int i = 0; i < G.vexnum - 1; ++ i) {
    //     int x = ans[i].first, y = ans[i].second;//将已经选择完成的边，放入最小生成树矩阵中
    //     minspatree_matrix[x][y] = minspatree_matrix[y][x] = G.arcs[x][y];
    // }
}

int main()
{
    AMGraph G;
    CreatGraph(G);
    MiniSpanTree(G);
    /*输出原始的矩阵*/
    // for (int i = 0; i < G.vexnum; ++ i) {
    //     for (int j = 0; j < G.vexnum; ++ j)
    //         cout << G.arcs[i][j] << ' ';
    //     cout <<endl;
    // }
    /*输出最小生成树的邻接矩阵*/
    // for (int i = 0; i < G.vexnum; ++ i) //cout << Vexset[i] << ' ';
    // {
    //     for (int j = 0; j < G.vexnum; ++ j)
    //         cout << minspatree_matrix[i][j] << ' ';
    //     cout << endl;
    // }

    system("pause");

    return 0;
}
/*
测试用例：
4 5
A B C D
0 1 3
0 3 4
1 2 6
2 3 7
1 3 5
*/

算法流程为：

1.将每条边（i，j，w）采用结构体方式保存，并进行排序。

2.选取剩余边中的最小边，将其加入到生成树中，并判断生成树是否结构合理，如果合理，继续选取下一条边，如果不合理，那也是继续选取下一条边，但是并不保留刚刚选取的数字。

3.重复2过程直到达到指定边数。

2.最短路问题

2.1 Dijstra算法

最短路问题的Dijstra算法我在这篇文章已经见过这里就不再赘述。

2.2 Floyd算法

我们都知道，Dijstra算法只能解决权重为真的图的最短路径，而Floya尽管时间复杂度（O(n³)）更高，但是其具有更少的缺点。

弗洛伊德是基于动态规划而构思的，弗洛伊德算法定义了两个二维矩阵：

矩阵D记录顶点间的最小路径
例如D[0] [3] = 10，说明顶点0 到 3 的最短路径为10；
矩阵P记录顶点间最小路径中的中转点
例如P[[0] [3] = 1 说明，0 到 3的最短路径轨迹为：0 -> 1 -> 3。

其代码为（代码来源）：

#include <stdio.h>
#include <stdlib.h>

#define MAXN 10 
#define INF = 1000

typedef struct struct_graph{
    char vexs[MAXN];
    int vexnum;//顶点数 
    int edgnum;//边数 
    int matirx[MAXN][MAXN];//邻接矩阵 
} Graph;

int pathmatirx[MAXN][MAXN];//记录对应点的最小路径的前驱点，例如p(1,3) = 2 说明顶点1到顶点3的最小路径要经过2 
int shortPath[MAXN][MAXN];//记录顶点间的最小路径值

void short_path_floyd(Graph G, int P[MAXN][MAXN], int D[MAXN][MAXN]){
    int v, w, k;
    //初始化floyd算法的两个矩阵 
    for(v = 0; v < G.vexnum; v++){
        for(w = 0; w < G.vexnum; w++){
            D[v][w] = G.matirx[v][w];
            P[v][w] = w;
        }
    }

    //这里是弗洛伊德算法的核心部分 
    //k为中间点 
    for(k = 0; k < G.vexnum; k++){
        //v为起点 
        for(v = 0 ; v < G.vexnum; v++){
            //w为终点 
            for(w =0; w < G.vexnum; w++){
                if(D[v][w] > (D[v][k] + D[k][w])){
                    D[v][w] = D[v][k] + D[k][w];//更新最小路径 
                    P[v][w] = P[v][k];//更新最小路径中间顶点 
                }
            }
        }
    }

    printf("\n初始化的D矩阵\n");
    for(v = 0; v < G.vexnum; v++){
        for(w = 0; w < G.vexnum; w++){
            printf("%d ", D[v][w]);
        }
        printf("\n");
    }

    printf("\n初始化的P矩阵\n");
    for(v = 0; v < G.vexnum; v++){
        for(w = 0; w < G.vexnum; w++){
            printf("%d", P[v][w]);
        }
        printf("\n");
    }

    v = 0;
    w = 3;
    //求 0 到 3的最小路径
    printf("\n%d -> %d 的最小路径为：%d\n", v, w, D[v][w]);
    k = P[v][w];
    printf("path: %d", v);//打印起点
    while(k != w){
        printf("-> %d", k);//打印中间点
        k = P[k][w]; 
    }
    printf("-> %d\n", w);
}

int main(){
    int v, w;
    Graph G;
    printf("请输入顶点数:\n");
    scanf("%d", &G.vexnum);
    printf("请输入初始矩阵值：\n");
    for(v = 0; v < G.vexnum; v++){
        for(w = 0; w < G.vexnum; w++){
            scanf("%d", &G.matirx[v][w]);
        }
    }
    printf("\n输入的矩阵值：\n");
    for(v = 0; v < G.vexnum; v++){
        for(w = 0; w < G.vexnum; w++){
            printf("%d ", G.matirx[v][w]);
        }
        printf("\n");
    }
    short_path_floyd(G, pathmatirx, shortPath);
}

弗洛伊德算法的核心在于，遍历每个结点，将每个结点作为中间结点，更新整个邻接图矩阵的最短路径。

for(k = 0; k < G.vexnum; k++){
    //v为起点 
    for(v = 0 ; v < G.vexnum; v++){
        //w为终点 
        for(w =0; w < G.vexnum; w++){
            if(D[v][w] > (D[v][k] + D[k][w])){
                D[v][w] = D[v][k] + D[k][w];//更新最小路径 
                P[v][w] = P[v][k];//更新最小路径中间顶点 
            }
        }
    }
}

2.3 spfa算法

SPFA算法是求解单源最短路径问题的一种算法，由理查德·贝尔曼（Richard Bellman）和莱斯特·福特创立的。有时候这种算法也被称为 Moore-Bellman-Ford 算法，因为 Edward F. Moore 也为这个算法的发展做出了贡献。它的原理是对图进行V-1次松弛操作，得到所有可能的最短路径。其优于Dijstra算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达 O(VE)。但算法可以进行若干种优化，提高了效率。

我们用数组dist记录每个结点的最短路径估计值，用邻接表或邻接矩阵来存储图G。

采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XVvgNYz8-1650418044143)(C:\Users\Lin\AppData\Roaming\Typora\typora-user-images\1650381541651.png)]

代码如下（代码来源）：

void Spfa(int s)
{
    flag=false;
    for(int i=0;i<maxn;i++)
        dis[i]=2e18;
    memset(vis,0,sizeof(vis));
    dis[s]=0,cont[s]=1;
    queue<int>q;
    q.push(s);
    while(q.size())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i;i=p[i].nxt)
        {
            int v=p[i].to;
            if(dis[v]>dis[u]+p[i].val)
            {
                dis[v]=dis[u]+p[i].val;
                cont[v]++;
                if(cont[v]>=n)
                {
                    flag=true;
                    break;
                }
                q.push(v);
            }
        }
    }
}

代码流程如下：

1.首先构建dis数组，起点赋值为0，其他节点均赋值为无穷大。将起点放入队列中。

2.随后开始循环，循环的判断条件为队列是否为空，当循环不为空，出栈一个元素，随后根据这个元素作为中间结点更新dis数组，如果更新了数组，就将该新的结点放入队列中。

3.重复执行2过程，直到队列为空。

3.最大流问题

3.1 什么是最大流问题

我们有图 G=(V, E)，V是顶点的集合，E是边的集合。
图中边的权重都为非负数 （满足1，2两点有时称之为流网络）。
对于这个图G，有两个顶点很重要，一个是源头s，一个是汇聚点t，我们想考虑的是从源头s流向汇聚点t的流。

我们可以知道有以下约束：

1.对于图中非s和t的普通结点，流进量等于流出量
2.我们非常关心总运输流量，比如这个下水道系统，究竟从s点到t点最多能运输多少立方米的水？我们把它记成|f|，这个|f|极其重要，是我们研究的目的所在。
3.当然，每条边是有运输上限的，就像某条公路车流是有上限的一样，若运输量无穷无尽，我们的研究也就没有意义了。我们将从u点到v点的运输上限，或者说是运载能力记为c(u,v)。对于从u点到v点的流量，记作f(u,v)。显然对所有边(u,v)我们有f(u,v)<=c(u,v)。

视图如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dH0H3mEU-1650418044143)(C:\Users\Lin\AppData\Roaming\Typora\typora-user-images\1650382272246.png)]

3.2 求解思路

（1）单纯形法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jEwxYanH-1650418044144)(C:\Users\Lin\AppData\Roaming\Typora\typora-user-images\1650382501521.png)]

本质上，最大流问题就是一个线性规划的问题，因此，求解过程中我们可以采用最原始的单纯形法进行求解，但是不太推荐，因为求解过程十分繁杂。

（2）标号法

这实际上是一种代码的思路，思路如下。

1.首先找到一个可行流，也就是满足所有条件的一个流，比如在上个图中每个路径选择流量均为0，在流的中间允许出现负回路。

2.找到一条可行支流，画图如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TYORDYVf-1650418044144)(file:///C:\Users\Lin\Documents\Tencent Files\2243197885\Image\C2C\CA81D926ECD575C448A0404D65E154BA.png)]

如图中的1-3-4-7和1-3-2-4-7都是可行支流。

3.随后对每个点进行逐一检测，计算标号值。

如果某一条路径为正路径，如1-3，theta = cij - fij，其中cij为路径最大承载，fij为实际承载。

如果某一条路径为负路径，如3-2，theta = fij。

4.随后计算某一条支流上的所有theta值，取最小值min（theta），为什么取最小，本质含义就是将支流中所有路径接近填满，但是又要防止某一条支流炸掉。

5.随后得到在图中选取新的可行流，重复2-4操作，直到没有还可以填充的可行流。

（3）割集与隔量

官方定义为割集是从网络发点到收点的一组弧的集合，从网络中去掉这组弧就断开了网络，发点将不能到达收点。

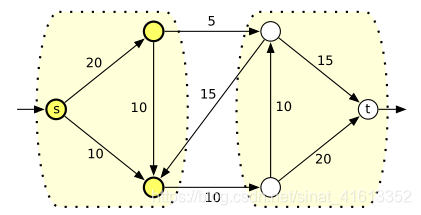
在这里插入图片描述

通俗来说，割集就是能把发点和收点断开的弧的组合。

如图所示，其中长度为5、10、15这块白色区域的弧所组成的路径（a，b）集合即为一个割集，割集中的割量也就是其路径对应容量之和。

定理：网络中的最大流量等于最小割量

这个其实很好理解，最小流量代表所有弧都能接受的一个总流量。

4.最小费用流

4.1 什么是最小费用流

在网络中的弧，不仅给出了容量，还有单位流量的费用。

可以将最小费用流问题分为两种类型：

1.固定流量下的最费用最小

2.最小费用最大流问题

4.2 求解最小费用流

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-m1IGA67o-1650418044145)(C:\Users\Lin\AppData\Roaming\Typora\typora-user-images\1650417730582.png)]

求解最小费用流的表达是一个很复杂的过程，这里就不说了。

我们主要采用的求解方法就是使用编程解决，可以看看这篇文章作为参考。

67o-1650418044145)]

求解最小费用流的表达是一个很复杂的过程，这里就不说了。

我们主要采用的求解方法就是使用编程解决，可以看看这篇文章作为参考。

林深时见鹿-1

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
运筹学网络模型

1.最小生成树1.1 什么是树？如果一个无向连通图不包含回路(连通图中不存在环),那么就是一个树。如下图所示即为一个数[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pm3hK7WV-1650418044140)(C:\Users\Lin\AppData\Roaming\Typora\typora-user-images\1650351532633.png)]1.2 什么是最小生成树最小生成树，顾名思义，就是在某个图结构中进行选取构造，构造出一个树。一个有N个点的图
复制链接

扫一扫