【数模】因子分析

声明：文章参考数学建模清风的网课编写。

因子分析简介

 因子分析由斯皮尔曼在1904年提出，其在某种程度上可以被看成主成分分析的推广和扩展。
 因子分析通过研究变量间的相关系数矩阵，把这些变量间错综复杂的关系归结成少数几个综合因子，由于归结出的因子个数少于原始变量的个数，但它们又几乎包含原始变量的全部信息，所以也是对原有数据的降维。
 由于因子往往比主成分更易得到解释，故因子分析比主成分分析更容易成功。

因子分析一般模型

 假设有n个样本，p个指标，构成大小为n*p的样本矩阵x:
$$x=\left[\begin{array}{cccc}{x}_{11}& x_{12}& ...& x_{1p}\\ x_{21}& x_{22}& ...& x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& ...& x_{np}\end{array}\right]=\left[\begin{array}{c}{x}_1,x_2,\dots ,x_p\end{array}\right]$$
 因子分析：
$$x_1,x_2,...,x_p\Rightarrow f_1,f_2,...,f_m(m\le p),$$ 且它们满足：$$\{\begin{array}{c}{x}_1=u_1+a_{11}{f}_1+a_{12}{f}_2+...+a_{1m}{f}_m+{\epsilon }_1\\ x_2=u_2+a_{21}{f}_1+a_{22}{f}_2+...+a_{2m}{f}_m+{\epsilon }_2\\ ⋮\\ x_p=u_p+a_{p1}{f}_1+a_{p2}{f}_2+...+a_{pm}{f}_m+{\epsilon }_p\end{array}$$
 其中$u_i$是$x_i$的均值，$a_{ij}$是$x_i$在因子$f_j$上的载荷，$f_1,f_2,...,f_m$被称为公共因子，${\epsilon }_i$被称为特殊因子，各因子的线性组合构成了原始的指标。注意：表示式中的每一个$x_i和f_i$都是一个包含n个元素的列向量。

 上述式子可以简记为：
$$x=u+Af+\epsilon$$
 其中:
$$A_{p\times m}=a_{ij},u=\left[\begin{array}{c}{u}_1\\ u_2\\ ⋮\\ u_p\end{array}\right],f=\left[\begin{array}{c}{f}_1\\ f_2\\ ⋮\\ f_m\end{array}\right],\epsilon =\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ ⋮\\ {\epsilon }_p\end{array}\right]$$
 并假设公共因子彼此步相关，且具有单位方差；特殊因子彼此不相关且与公共因子不相关。

因子分析有几个比较重要的数据需要重点说明一下：

• $A$被称为因子载荷矩阵；
• $A$的行元素平方和$h_i^2={\sum }_{j=1}^m{a}_{ij}^2$表示原始变量$x_i$对公共因子的依赖程度，被称为共性方差；
• $A$的列元素平方和$g_i^2={\sum }_{i=1}^p{a}_{ij}^2$表示公因子$f_j$对x的贡献；

因子分析步骤

1. 将数据导入SPSS后点击分析->降维->因子：
   

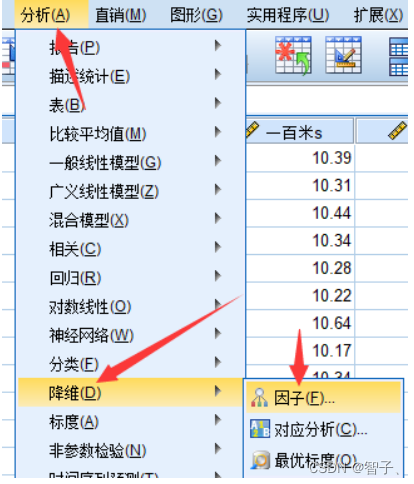
2. 选择要分析的变量：
   

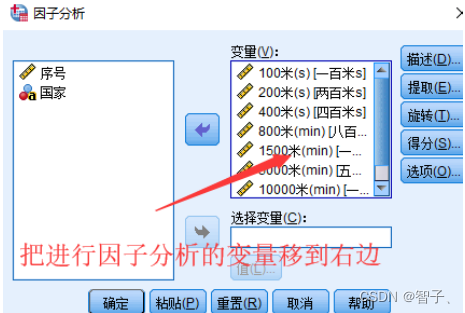
3. 在第2步页面，单击右侧描述并按图进行勾选：
   

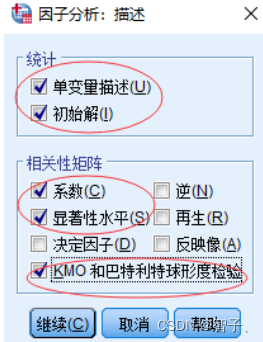
   单变量描述：输出参与分析的每个原始变量的均值、标准差和有效取值个数。
   初始解：输出未经过旋转直接计算得到的初始公因子、初始特征值和初始方差贡献率等信息。
   系数：输出初始分析变量间的相关系数矩阵。
   显著性水平：输出每个相关系数对于单侧假设检验的显著性水平。
   KMO检验和巴特利特球形检验：进行因子分析前要对数据进行KMO检验和巴特利特球形检验。简单来说KMO检验标准：KMO>0.9,非常适合；0.8<KMO<0.9,适合；0.7<KMO<0.8, 一般；0.6<KMO<0.7,不太适合；KMO<0.5,不适合。巴特利特球形检验显著值小于0.05。

4. 在第2步页面，单击右侧提取并按图依次选择。注意此步中没有选择要提取因子数，需要经过一次分析观察碎石图选择合适的因子数。
   

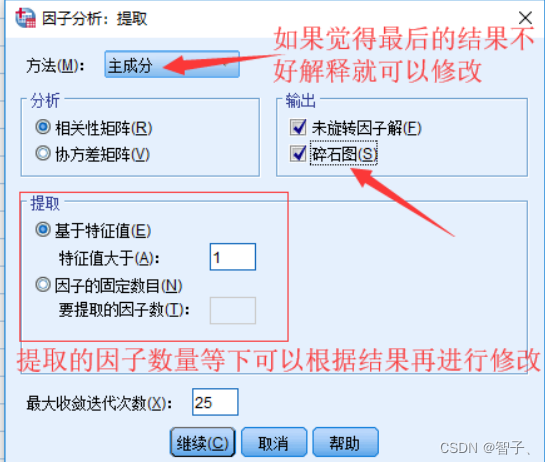
5. 在第2步页面，单击右侧旋转并按图依次选择：
   

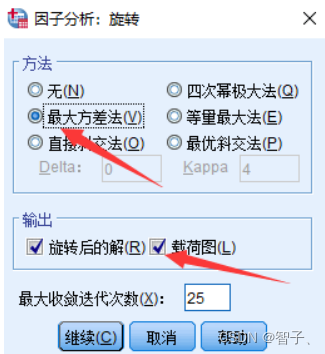
6. 在第2步页面，单击右侧得分并按图依次选择：
   

7. 确定因子数目：
   碎石检验（scree test）是根据碎石图来决定因素数的方法。Kaiser提出，可通过直接观察特征值的变化来决定因素数。当某个特征值较前一特征值的值出现较大的下降，而这个特征值较小，其后面的特征值变化不大，说明添加相应于该特征值的因素只能增加很少的信息，所以前几个特征值就是应抽取的公共因子数。

   从碎石图可以看出，前两个因子对应的特征值的变化较为陡峭，从第三个因子开始，特征值的变化较为平坦，因此我们应选择两个因子进行分析。（SPSS中文版翻译成了组件，实际应翻译为因子）。
   

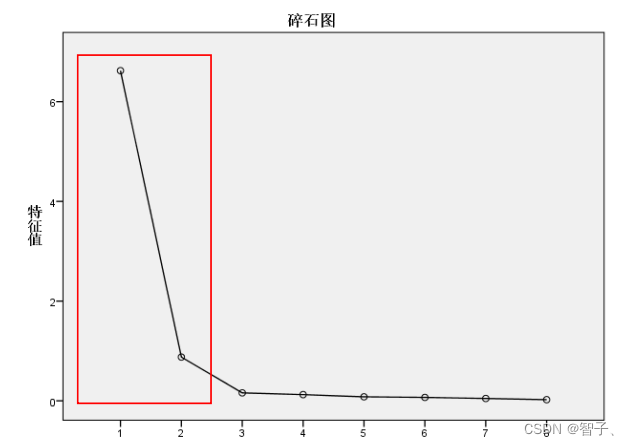
8. 根据第7步确定好的因子数重新进行因子分析得出最终结果。

因子分析结果解释

1. 数据是否适合因子分析(如图KMO>0.9，并且巴特利球形检验显著性<0.05。非常适合。)：
   

2. 公因子方差，即共性方差。载荷矩阵$A$的行元素平方和$h_i^2={\sum }_{j=1}^m{a}_{ij}^2$表示原始变量$x_i$对公共因子的依赖程度。
   
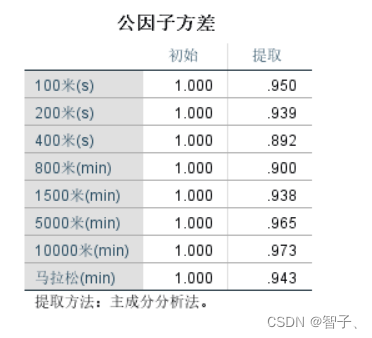
   100米(s)这个变量的公因子方差为0.95，这可以解释为我们提取的两个公共因子对100米(s)这个变量的方差贡献率为95%，即这两个公共因子能够反映出（或者说保留）100米(s)这个变量95%的信息。

3. 总方差解释。
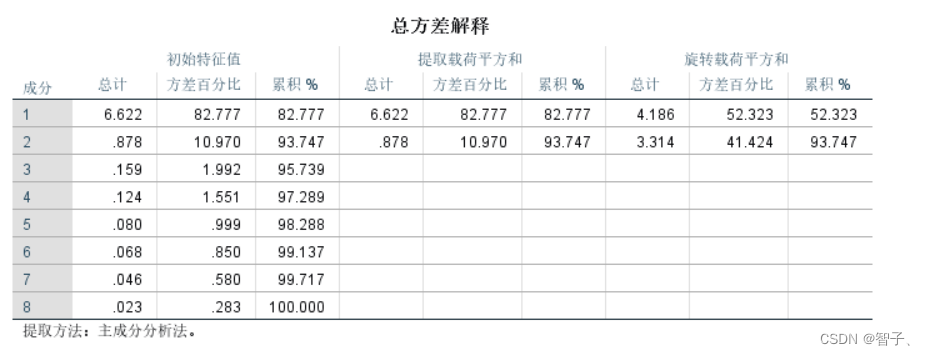   从“初始特征值”一栏中可以看出，前2个公共因子解释的累计方差达93.747%，而后面的公共因子的特征值较小，对解释原有变量的贡献越来越小，因此提取两个公共因子是合适的。
   “提取载荷平方和” 一栏是在未旋转时被提取的2个公共因子的方差贡献信息，其与“初始特征值”栏的前两行取值一样。
   “旋转载荷平方和”是旋转后得到的新公共因子的方差贡献信息，和未旋转的贡献信息相比，每个公共因子的方差贡献率有变化，但最终的累计方差贡献率不变

4. 成分矩阵，即载荷矩阵$A$。
   注意：只解释旋转后的成分矩阵。因为旋转的作用使得旋转后的矩阵更容易解释。
   
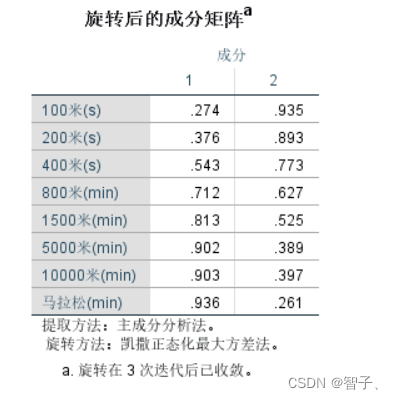
   因子1（SPSS翻译为成分）在后5个变量的绝对值取值较大；因子2在前三个变量的绝对值取值较大。因此因子1可以解释为耐力因子，因子2可以解释为爆发力因子。

5. 成分得分系数矩阵。
   先来解释一下得分：
   因子分析是将变量表示为公共因子和特殊因子的线性组合；此外，我们可以反过来将公共因子表示为原变量的线性组合，即可得到因子得分。
   $$\{\begin{array}{c}{x}_1=u_1+a_{11}{f}_1+a_{12}{f}_2+...+a_{1m}{f}_m+{\epsilon }_1\\ x_2=u_2+a_{21}{f}_1+a_{22}{f}_2+...+a_{2m}{f}_m+{\epsilon }_2\\ ⋮\\ x_p=u_p+a_{p1}{f}_1+a_{p2}{f}_2+...+a_{pm}{f}_m+{\epsilon }_p\end{array}$$$$\Downarrow$$$$\{\begin{array}{c}{f}_1=b_{11}{x}_1+b_{12}{x}_2+...+b_{1p}{x}_p\\ f_2=b_{21}{x}_1+b_{22}{x}_2+...+b_{2p}{x}_p\\ ⋮\\ f_m=b_{m1}{x}_1+b_{m2}{x}_2+...+b_{mp}{x}_p\end{array}$$
   $b_{ij}$就是第i个因子$f_i$对应于第j个变量$x_j$的系数。

   因子分析的结果就是由$b_{ij}$构成的$B_{m\times p}$系数矩阵。
   

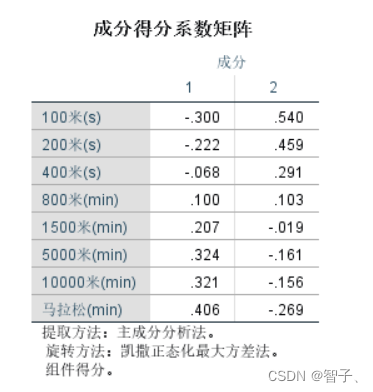
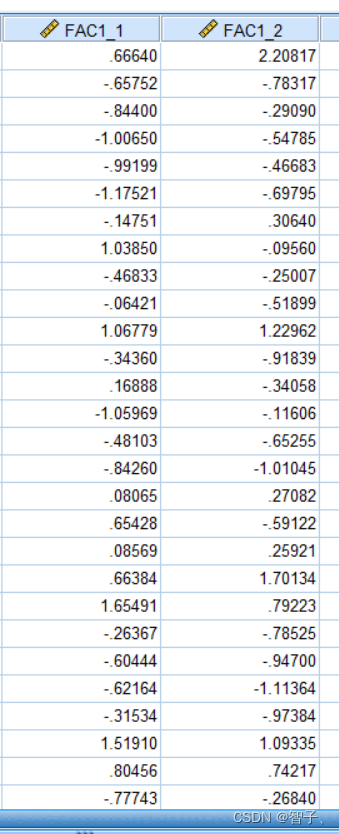
   使用因子分析结果，可以计算因子。(图中的因子是SPSS计算好的)