MINIEYE杯第十六届华中科技大学程序设计邀请赛 补题

D Difference

题意：

函数$f(l,r)=max(a[l],a[l+1],...a[r])-min(a[l],a[l+1],...a[r])\ast (r-l+1)$
给定一个长度为n的数组a,求其中第k大的权值。

思路

个人认为题目没有说清楚，例如 1 1 同属第一大。实际一个为第一大，另一个1为第二大。（可能是自己太菜了）
经典求第k大的数。
尝试二分O(nlogv)
可以发现f(l, r) < f(l, r + 1) < f(l, r + 2)… < f(l, n)
因为假设左边界l固定，随着r增大，那么要么会使得max增大，要么会使得min减小，或者都不变。
单独一个max增大，会使得（max - min)增大，且(r - l + 1)也会增大。
同理
f(l, r)固定左边界l，那么随着r增大，f(l,r)单调递增。 k = 2
考虑如何去check(mid)是否有 >= k个 >= mid值的数字的右区间。
0 0 0 2 5 7
为何不去check()是否有>= k -1 个 > mid大的数字的右区间？
因为要二分的mid，不知道是否在序列中出现过，假设没有出现过，那么会导致二分的mid出现错误，例如K = 2,会得到ans = 6。假设按照>=k check, 那么暗含一个在序列中出现过的数。得到的答案ans = 5。
如何check？
因为每个l都有对应的 f(l, r) >= mid的一个r，那么每个r相加即可。
直接双指针扫描即可。

code

using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int maxn = 5e5 + 10;
typedef pair <int, int> PII;
ll a[maxn], k;ll n;
int lg[maxn], f1[maxn][20], f2[maxn][20];
void init()
{
    lg[1] = 0, lg[2] = 1;
    for(int i = 3 ; i <= maxn - 10; i ++)
    lg[i] = lg[i >> 1] + 1;
}
void ST()
{
    init();
    for(int j = 0 ; j <= 19 ; j ++)
    {
        for(int i = 1 ; i + (1 << j) - 1 <= n ; i ++)
        {
            if(!j) 
            {
                f1[i][j] = a[i], f2[i][j] = a[i];
            }
            else
            {
                f1[i][j] = max(f1[i][j - 1], f1[i + (1 << j - 1)][j - 1]), f2[i][j] = min(f2[i][j - 1], f2[i + (1 << j - 1)][j - 1]);
            }
        }
    }
}
PII query(int l, int r)
{
    int k = lg[r - l + 1];
    return {max(f1[l][k], f1[r + 1 - (1 << k)][k]), min(f2[l][k], f2[r + 1 - (1 << k)][k])};
}
ll cal(int l, int r)
{
    PII temp = query(l, r);
    return (temp.first - temp.second) * 1ll * (r - l + 1) * 1ll;
}
bool check(ll mid)
{
    ll cnt = 0;
    int j = 1;
    for(int i = 1 ; i <= n ; i ++)
    {
        if(i > j)
        j = i;
        while(j <= n && cal(i, j) <= mid)
        j ++;// j > n  || cal(i,j) >= mid 
        cnt += (j - i) * 1ll;
    }
    if(cnt >= k)
    return true;
    else return false;
}
int main()
{
    scanf("%lld %lld", &n, &k);
    k = n * (n + 1) / 2 - k + 1; //比当前mid小的数 
    ll maxx = -INF, minn = INF;
    for(int i = 1 ; i <= n ; i ++)
    scanf("%lld", &a[i]), maxx = max(maxx, a[i]), minn = min(minn, a[i]);
    ST();
    ll l = 0, r = (maxx - minn) * n * 1ll;
    while(l < r)
    {
        ll mid = (l + r) >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    printf("%lld\n", l);
    return 0;
}

H Permutation Counting

题意：

给定n个点和m个关系。关系表示为(x, y)且对于每个关系x都是不同的，要满足p[x] < p[y],求满足关系的1–n的全排列有多少个。

思路：

首先注意存在无解情况，即每对关系间进行建边，有环且表示无解。那么有向图判环，直接拓扑排序就好了， 假设一开始建边x–>y。
其次考虑有解情况，由于一开始建边x–>y,且有解，那么说明本图是DAG。假设按照拓扑序进行DP求解。会影响到题意。
例如
4 3
1 2
3 2
2 4

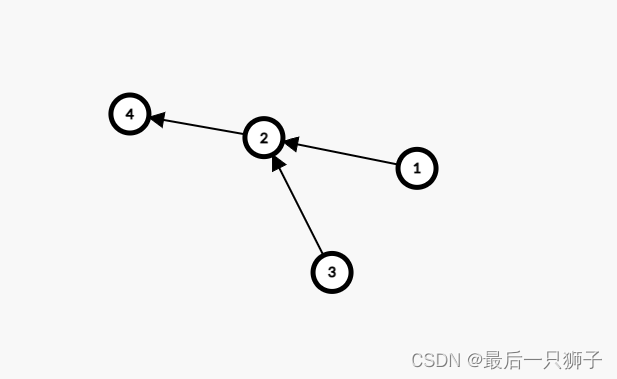
可以发现假设按照拓扑序来求，1 – > 3 – > 2 – > 4或者 3 --> 1 – > 2 – > 4
可以发现1号点和3号点不存在大小关系。无法按照这样来求解。
之后发现题目中说明了每对关系(x, y)中x保证不同，假设按照y – > x，说明每个节点都最多只有一个父节点又考虑到是一个有向图且无环，那么就是树形图。原来那种建图方式（x --> y) 表明每个节点可有>1个的父节点。
为了方便计算，可以新建一个虚拟源点0号点，和所有入度为0的点建边。那么就把本题转化为了树上问题。

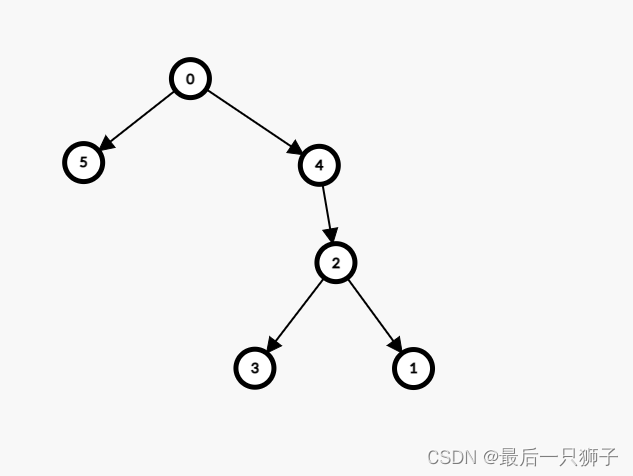
建出一个树形图之后，就可以进行树形DP求解。
f[i]：表示不考虑i号点且子树内的点随便从全排列中选所有合法的方案。
属性：cnt
状态计算：
$sum:当前节点u的子树大小（包含节点u），son为u的儿子节点$
$f[u]=f[u]\ast f[son]\ast C_{sum-1}^{siz[son]},sum-=siz[son]$

code：

const int maxn = 2e6 + 10;
typedef pair <int, int> PII;int n, m;
int h[maxn], ne[maxn * 2], e[maxn * 2], idx, in[maxn], siz[maxn];
ll f[maxn], fact[maxn], infact[maxn];
const ll mod = 998244353;
ll get_mod2(ll a, ll b)
{
	return (a % mod * (b % mod)) % mod;
}
ll ksm(ll base, ll power)
{
	ll res = 1;
	while(power)
	{
		if(power & 1)
		res = res * base % mod;
		base = base * base % mod;
		power >>= 1;
	}
	return res;
}
void init()
{
    fact[0] = infact[0] = 1;
    for (int i = 1; i <= n; i++) 
	{
        fact[i] = fact[i - 1] * i % mod;
        infact[i] = infact[i - 1] * ksm(i, mod - 2) % mod;
    }
}
ll get_c(int n, int m)
{
	if(n < m || n < 0 || m < 0) return 0;
	return 1ll * fact[n] * infact[m] % mod * infact[n - m] % mod;
}
void add(int u, int v)
{
	e[idx] = v;
	ne[idx] = h[u];
	h[u] = idx ++;
}
bool topsort()
{
	queue <int> alls;
	int cnt = 0;
	vector <int> ALLS;
	for(int i = 1 ; i <= n ; i ++)	
	{
		if(in[i] == 0) //入度为0的点进队 所有的起点 
		alls.push(i), cnt ++, ALLS.push_back(i);
	}
	while(!alls.empty())
	{
		int temp = alls.front();
		alls.pop();
		for(int i = h[temp] ; i != -1; i = ne[i])
		{
			int son = e[i];
			in[son] --;
			if(in[son] == 0)
			{
				alls.push(son);
				cnt ++;
			}
		}
	}
	for(auto t : ALLS)
	add(0, t); //
	if(cnt == n)
	return true; //拓扑序 
	else return false;
}
void dfs(int sta) 
{
	siz[sta] = 1;
	for(int i = h[sta] ; i != -1; i = ne[i])
	{
		int son = e[i];
		dfs(son);
		siz[sta] += siz[son];
	}
}
void dfs1(int sta)
{
	f[sta] = 1;
	int temp = siz[sta]; //子树中所有点 
	for(int i = h[sta] ; i != -1 ; i = ne[i])
	{
		int son = e[i];
		dfs1(son); //
		f[sta] = get_mod2(f[sta], get_mod2(f[son], get_c(temp - 1, siz[son])));
		temp -= siz[son];
	}
}
int main()
{
	scanf("%d %d", &n, &m);
	memset(h, -1, sizeof(h)), idx = 0;
	init(); //预处理组合数 
	for(int i = 1 ; i <= m ; i ++)
	{
		int u, v;
		scanf("%d %d", &u, &v); // u --> v
		in[u] ++;  //入度为0 
		add(v, u);
	}
	if(topsort())
	{
		dfs(0);
		dfs1(0);
		printf("%lld\n", f[0] % mod);
	}
	else printf("0\n");
	return 0;
}