堆及堆排序（超超超超超详细讲解~~~~）-----数据结构

1.堆的概念及结构

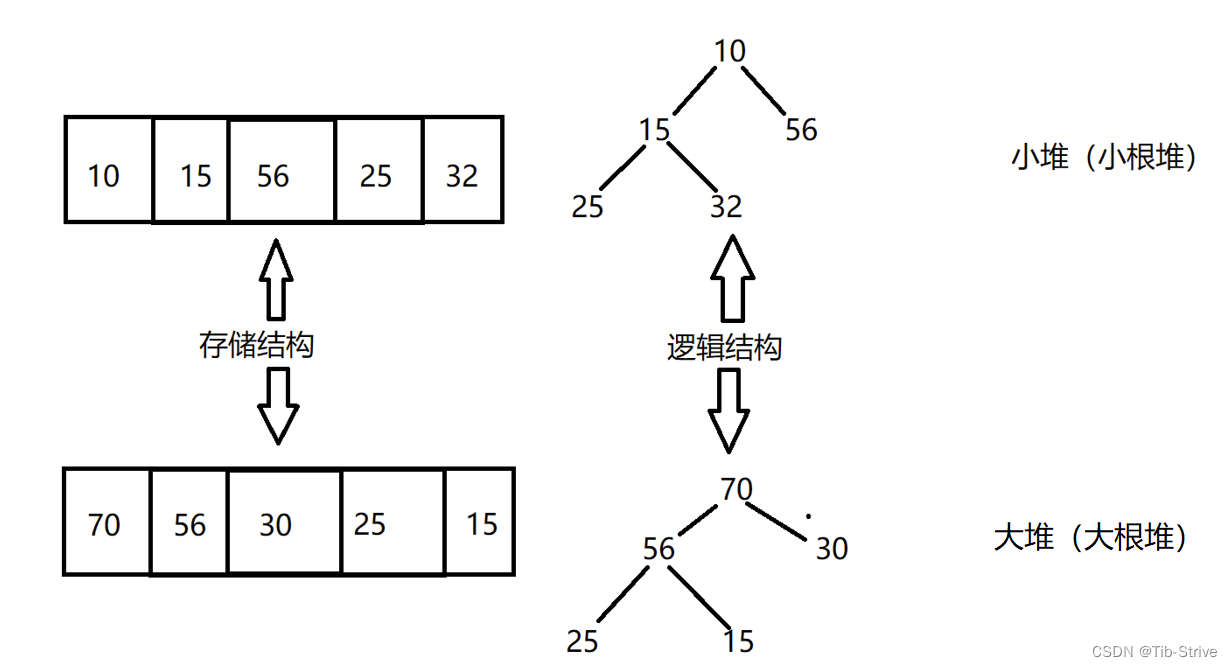
将一个关键码的集合K={k0,k1,k2, … ,k n-1},把它所有元素按照完全二叉树的顺序存储方式存储在一个一维数组中，且该完全二叉树满足每个父节点大于（小于）其左右孩子节点，则称为大堆（小堆）。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆

堆的性质：
~堆中每个节点的值总是不大于或不小于其父节点的值
~堆总是一棵完全二叉树

2.堆的实现

补充：代码中的传参的CpSize compare为比较函数的函数指针变量

typedef int HeapType;//堆中元素类型的重命名（利于修改堆中元素类型的修改）
typedef int (*CpSize)(HeapType x, HeapType y);//比较函数的函数指针类型重命名
int Max(HeapType x, HeapType y)
{
	return x > y;
}
int Min(HeapType x, HeapType y)
{
	return x < y;
}
//函数传参根据建大堆或小堆传Max或Min即可

2.1 堆的两种基本算法

堆的两种的基本算法：堆的向下调整算法（用于建堆和堆删除），堆的向上调整算法（用于元素插入）

2.1.1堆的向下调整算法

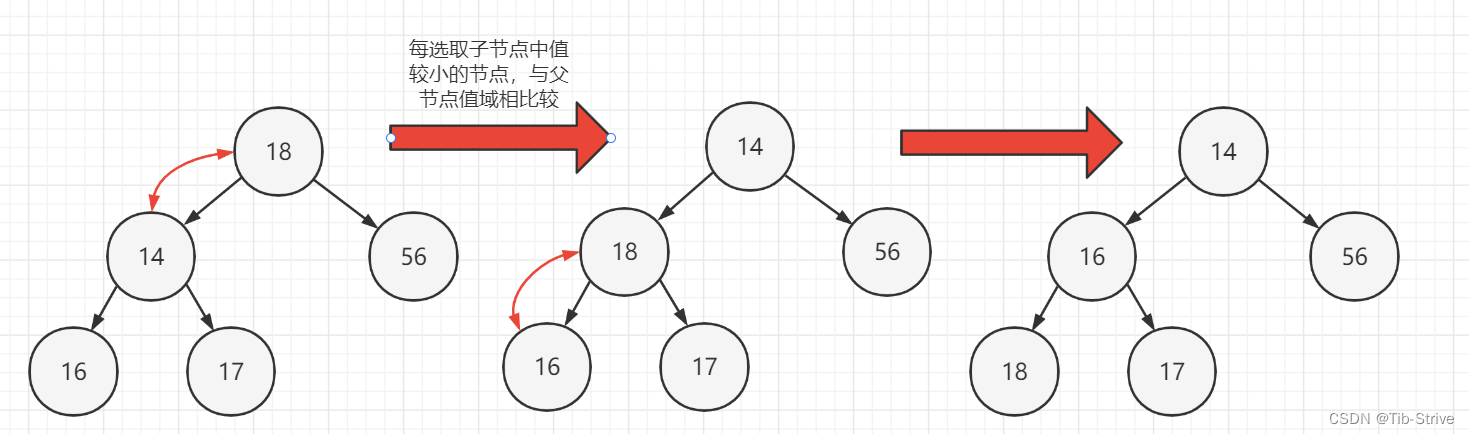
前提：左右子树必须是一个堆，才能调整
给定一个数组，其逻辑上看做一棵完全二叉树，从根节点开始的向下调整算法可以把它调整为一个小堆。

int array [] = { 18 , 14 , 56 , 16 , 17 }; (建小堆)

//向下调整算法
//假设下标以parent的父节点，左右子树均满足堆结构的情况下，而实现的算法
void AdjustDown(Heap* hp, int parent,CpSize compare)
{
	assert(hp);
	int child = parent * 2 + 1;
	int size = hp->size;
	while (child<size)
	{
		if (child+1<size&&hp->compare(hp->arr[child+1],hp->arr[child]))
		{
			child += 1;
		}
		if (hp->compare(hp->arr[child],hp->arr[parent]))
		{
            Swap(hp->arr + child, hp->arr + parent);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			return;
		}
	}
}

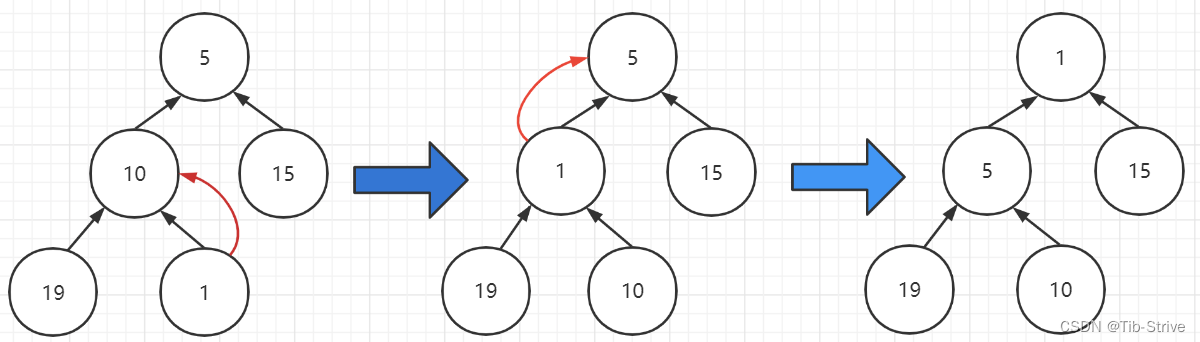
2.1.2堆的向上调整算法

向上调整算法，意在与插入元素于数组末尾会破坏堆结构，因而从底至上调整元素位置

int arr [] ={ 5, 10 , 15 , 19};
插入元素 1 之后

//从最后一个非叶子节点开始，向上调整
void AdjustUp(Heap* hp,int child,CpSize compare)
{
	assert(hp);
	int parent = (child - 1) / 2;
	//child从最后一个元素下标（可得最后一个非叶子节点的下标）开始递减
	while (parent>=0)
	{
		if (hp->compare(hp->arr[child], hp->arr[parent]))
		{
			Swap(hp->arr + child, hp->arr + parent);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
		   return;
		}
	}
}

2.2 堆的创建

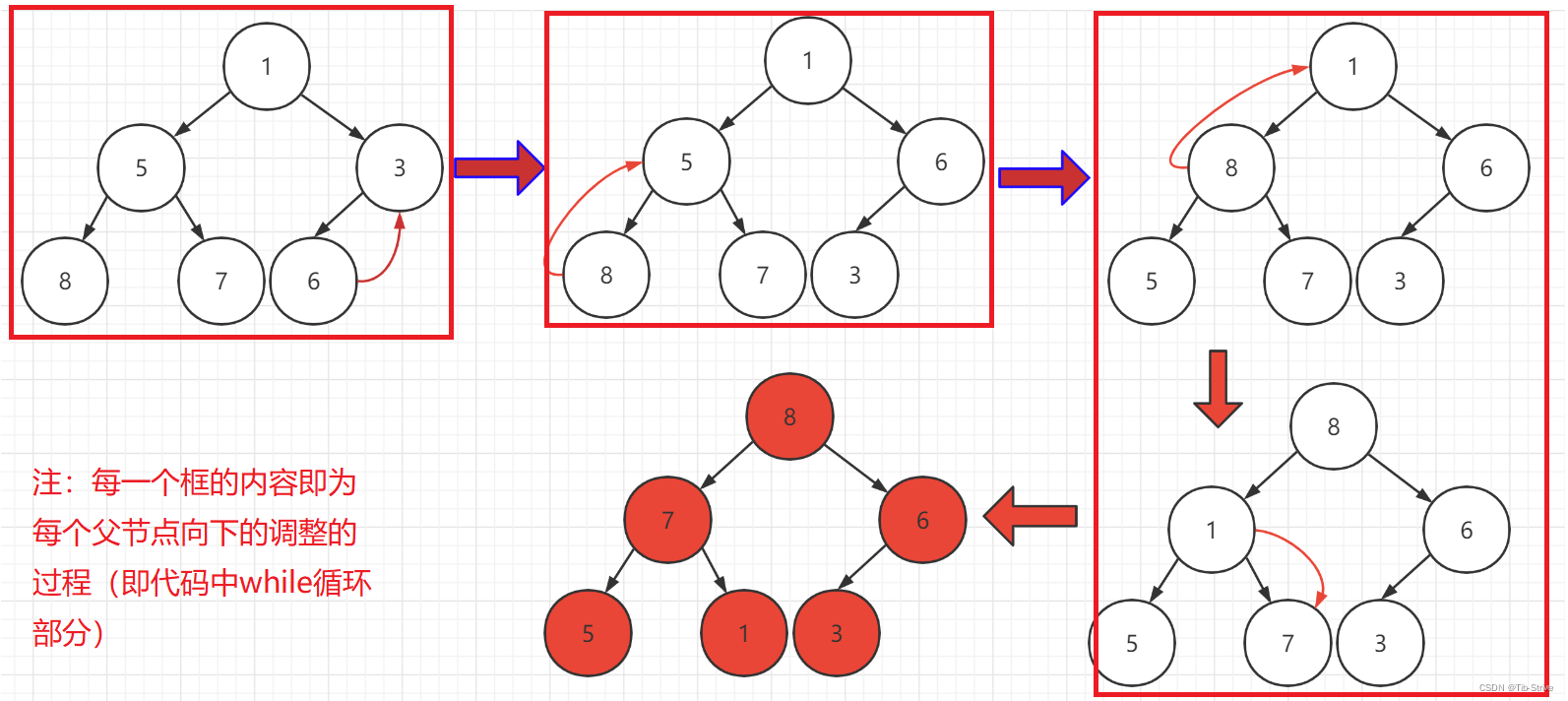
由二叉树本身的递归构造性质以及向下调整算法可知，我们可由最后一个非叶子节点（落实于n元素数组中，即下标为（n-1）/2的元素）开始——即满足了堆左右子树堆结构的前提条件，进行向下调整算法，逐步构成大堆的子结构（建大堆）

int array []={ 1, 5, 3 , 8, 7, 6};(大堆)

//堆的构建
void   HeapCreate(Heap* hp, HeapType* arr, int n,CpSize compare)
{
	assert(hp);
	hp->capacity = n;
	hp->size = 0;
	HeapType* a_ = (HeapType*)malloc(sizeof(HeapType) * hp->capacity);
	if (a_ == NULL)
	{
		assert(a_);
		return;
	}
	hp->arr = a_;
	memcpy(hp->arr,arr,sizeof(HeapType)*n);
	hp->size = n;
	hp->compare = compare;
	for (int root = (hp->size - 2) / 2; root >= 0; root--)
	{
		AdjustDown(hp, root,compare);
	}
}

2.3堆的插入

思想：将元素插入数组中的最后一个元素（即完全二叉树中的最后一个节点），在进行向上调整算法，直到满足堆

图片信息可参照向上调整内容！！！

注：不知道是否有铁铁产生过为什么不能使用向下调整法来解决插入问题的疑惑！！！！
实则因为在插入元素之后破坏了堆左右子树为堆结构的前提条件，故便不能是向下调整法来解决插入问题

//扩容
void HeapCheakCapacity(Heap* hp)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		HeapType* cur = (HeapType*)realloc(hp->arr, sizeof(HeapType) * hp->capacity * 2);
		if (cur == NULL)
		{
			printf("realloc");
			return;
		}
		hp->arr = cur;
		hp->capacity *= 2;
	}
}
//堆的插入
void   HeapPush(Heap* hp, HeapType x)
{
	HeapCheakCapacity(hp);
	hp->size++;
	hp->arr[hp->size - 1] = x;
	//向上调整
	AdjustUp(hp, hp->size - 1,hp->compare);
}

2.4堆顶元素的删除

将堆顶元素与最后一个元素进行置换，之后删除最后一个元素，再通过向下调整算法实现堆的删除。

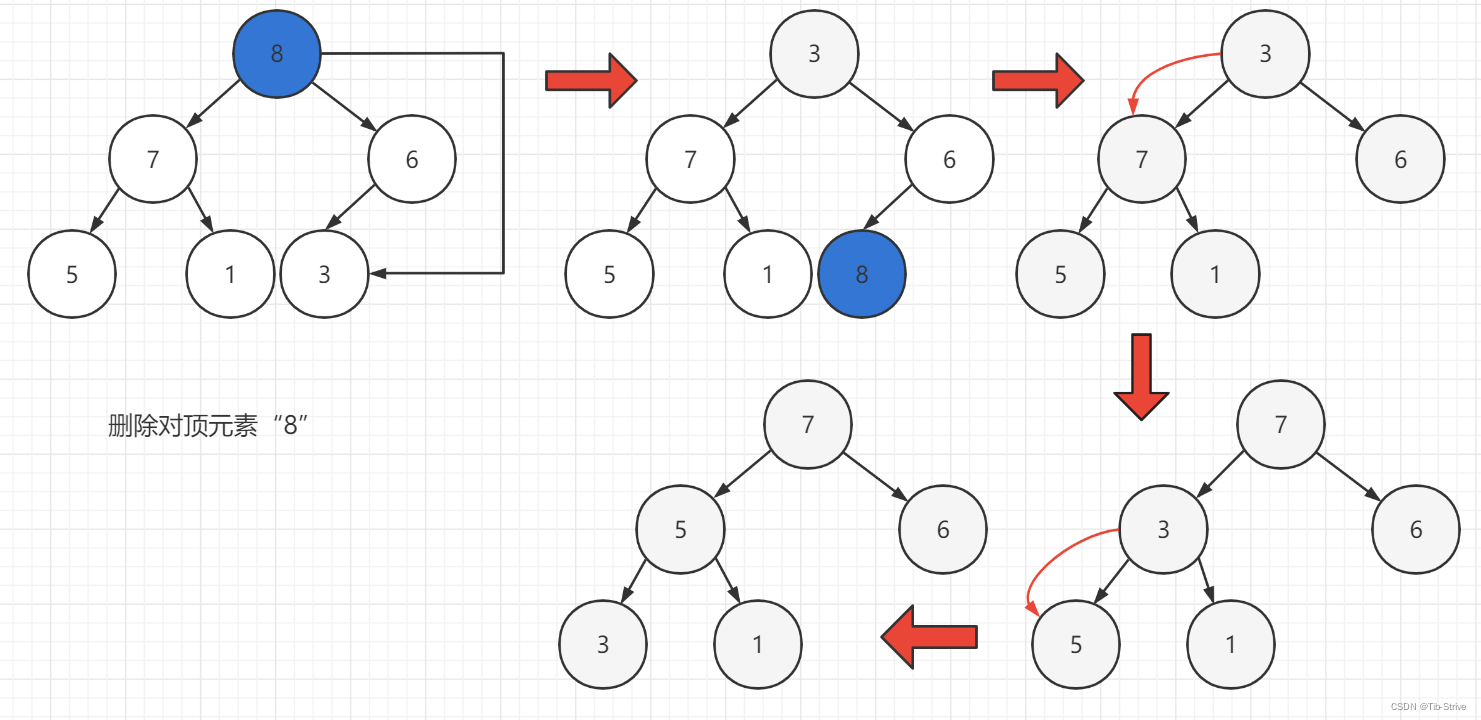
//堆的删除(删除堆顶元素)
void   HeapPop(Heap* hp)
{
	if (HeapEmpty(hp))
	{
		return;
	}
	HeapCheakCapacity(hp);
	Swap(hp->arr + 0, hp->arr + (hp->size - 1));
	hp->size--;
	AdjustDown(hp, 0,hp->compare);
	//AdjustUp(hp, hp->size - 1,hp->compare);---错误，因为修改堆顶元素和堆底元素将不满足堆结构
}

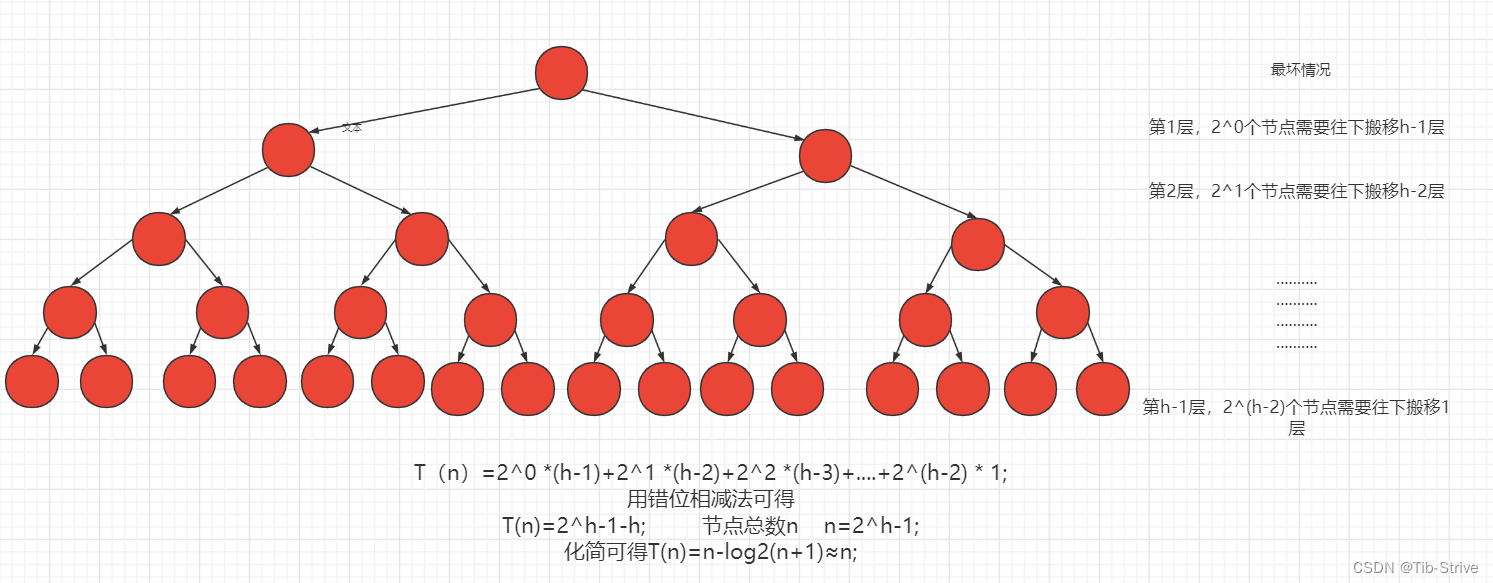
2.4建堆的时间复杂度

建堆的时间复杂度为O（n）；

堆为完全二叉树，满二叉树也为完全二叉树的一种特殊情况（满二叉树不影响堆时间复杂度的计算）

3.堆的应用

3.1堆排序

堆排序即利用堆的思想来进行排序，分为两个步骤

1. 建堆
   -----升序：建大堆
   -----降序：建小堆
   2.利用堆删除思想来进行排序
   图形展示

int array[]={ 1 , 5 , 3 , 8 , 7 , 6};
始图为建堆完成时，逻辑结构图（可参照上述建堆过程）

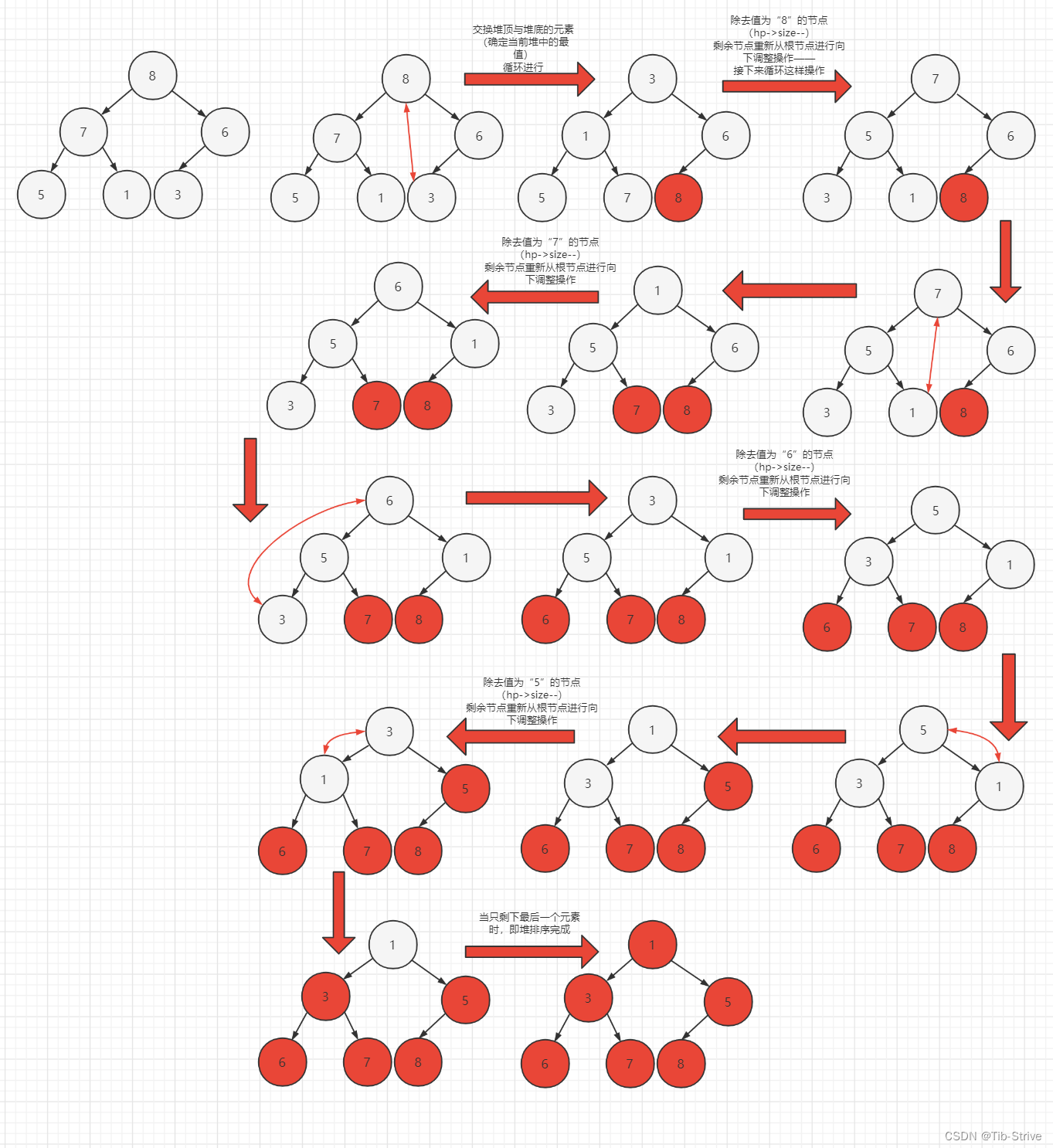
//堆排序
void HeapSort(Heap* hp,CpSize compare)
{
	int child = hp->size - 1;
	int size = hp->size;
	while (child)
	{
		Swap(hp->arr + 0, hp->arr + child);
		hp->size--;
		AdjustDown(hp, 0, compare);
		child--;
	}
	hp->size = size;
}