马栏过河卒动态规划算法

题目

• 棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。
  【输入】
  给出n、m和C点的坐标。
  【输出】
  从A点能够到达B点的路径的条数。
  【输入样例】
  8 6 0 4
  【输出样例】
  1617

算法设计思路

1.初始化棋盘(外围赋值零 防止数组越界)使每一个都位置都是位置初始化使得每个点都是1.

0	0	0	0	0	0	0	0	0
0	1	1	1	1	1	1	1	0
0	1	1	1	1	1	1	1	0
0	1	1	1	1	1	1	1	0
0	1	1	1	1	1	1	1	0
0	1	1	1	1	1	1	1	0
0	1	1	1	1	1	1	1	0
0	1	1	1	1	1	1	1	0
0	0	0	0	0	0	0	0	0

2.设置马的方向{(-1,-2),(-1,2),(1,2),(1,-2),(2,1),(-2,-1),(-2,1)
,(2,-1)},以及马(4.4)的自己的坐标，将这九个个坐标进行标记（以下只展示未越界部分）

1	1	1	1	1	1	1
1	1	0	1	0	1	1
1	0	1	1	1	0	1
1	1	1	0	1	1	1
1	0	1	1	1	0	1
1	1	0	1	0	1	1
1	1	1	1	1	1	1

3.清楚兵的走法{(0,+1),(+1,0)}
4…设置初态dp(1,1)=1
5,利用兵的走法设置状态方程

根据以上方程式,测试一些数据所得的结果如下

1	1	1	1	1	1	1
1	2	0	1	0	1	2
1	0	0	1	1	0	2
1	1	1	0	1	1	3
1	0	1	1	2	0	3
1	1	0	1	0	0	3
1	2	2	3	3	3	6

代码部分

初始化

设置二维数组Dp[][]存储该点走过的次数，hoget存储马的行走方向。

int dp[N][N] = { 0 };
Int hoget[8][2]= { { -1,-2},{ -1,2},{1,2},{1,-2},{2,1},{ -2,-1},{ -2,1},{2,-1}  };

设置马的跳跃点及马的初始位置

根据马的跳跃方向设置兵不能走的地方，将其所在位置的数值赋成零。

int  hourse(int (*dp)[N], int(*hoget)[2], int hx,int hy) {
	dp[hx][hy] = 0;
	for (int j = 0;j < 8;j++) {
		if(hoget[j][0]+hx>0&&hoget[j][1]+hy>0)//防止数组越界
		  dp[hoget[j][0] + hx][hoget[j][1] + hy] = 0;
	}
	return 0;
}//设置兵不能走的位置

马拦过河卒算法

将每一个点遍历，遍历时该点的经过次数是左边和上面数组中值之和

int solve(int (*dp)[N], int x,int y) {
	int i, j;
	for (i = 1;i <= x;i++) {
		for ( j = 1;j <= y;j++) {
			if(dp[i][j]!=0) {//排除不能走的位置
			  if (i == 1 && j == 1)
				dp[1][1] = 1;//设置初始状态
			  else
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
			printf("%d\t", dp[i][j]);
		}
		printf("\n");
	}
	return 0;
}

运行结果

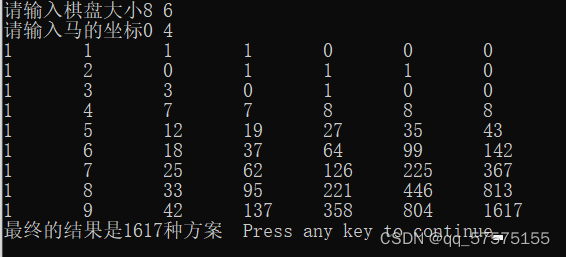
所有代码

#include<stdio.h>
#define N 100
#pragma warning (disable:4996) 

int initial(int (*dp)[N],int x, int y) {
	for (int i = 1;i <= x;i++) {
		for (int j = 1;j <= y;j++) {
			dp[i][j] = 1;
		}
	}//防止slove中数组的越界，在外围赋值零
	return 0;
}//初始化棋盘

int  hourse(int (*dp)[N], int(*hoget)[2], int hx,int hy) {
	
	dp[hx][hy] = 0;
	for (int j = 0;j < 8;j++) {
		if(hoget[j][0]+hx>0&&hoget[j][1]+hy>0)//防止数组越界
		  dp[hoget[j][0] + hx][hoget[j][1] + hy] = 0;
	}
	return 0;

}//设置兵不能走的位置
  
int solve(int (*dp)[N], int x,int y) {
	int i, j;
	for (i = 1;i <= x;i++) {
		for ( j = 1;j <= y;j++) {
			if(dp[i][j]!=0) {//排除不能走的位置
			  if (i == 1 && j == 1)
				dp[1][1] = 1;//设置初始状态
			  else
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
			printf("%d\t", dp[i][j]);
		}
		printf("\n");
	}
	return 0;
}
int main() {
	int dp[N][N] = { 0 };
	int hoget[8][2] = { { -1,-2},{ -1,2},{1,2},{1,-2},{2,1},{ -2,-1},{ -2,1},{2,-1} };
	int x, y, hx, hy;
	printf("请输入棋盘大小");
	scanf("%d%d", &x, &y);//输入棋盘大小
	printf("请输入马的坐标");
	scanf("%d%d", & hx, & hy);//s输入马的坐标
	initial(dp,x+1, y+1);//+1是增加了一层为零的围墙，初始化棋盘
	hourse(dp,hoget,hx+1,hy+1);//增加不可走点
	solve(dp,x+1, y+1);//计算每个位置走过的次数
	printf("最终的结果是%d种方案\t", dp[x+1][y+1]);
	return 0;
}