Prim算法和Kruskal算法都是用于找到加权连通图的最小生成树，但策略不同。Prim算法从一个顶点开始，每次添加最近的未连接顶点，而Kruskal则是按权重排序边并避免形成环。Kruskal在效率上优于Prim，因为它只需一次排序。文章提供了两个算法的Java实现例子，并给出了一道相关编程题的解题思路。
Prim和Kruskal有啥区别？到底哪个好？
今天做了一道最小生成树的题，发现了一点猫腻！
题目在这里 ： 《修路问题1》
先说结论
Prim算法 和 Kruskal算法 都是从连通图中找出 最小生成树 的经典算法～
从策略上来说，Prim算法是直接查找，多次寻找邻边的权重最小值，而 Kruskal是需要先对权重排序后查找的 ～
所以说，Kruskal在算法效率上是比Prim快的 ，因为Kruskal只需一次对权重的排序就能找到最小生成树，而Prim算法需要多次对邻边排序才能找到～
Prim
Prim算法是一种产生最小生成树的算法。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；
并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。
Prim算法从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪婪算法。朴素版时间复杂度为：O(n²) ，堆优化过后的prim时间复杂度为O(mlogn)。
算法描述：
- 在一个加权连通图中，顶点集合V，边集合为E
- 任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离，选择距离最短的，标记visit.
- 重复以下操作，直到所有点都被标记为visit：
在剩下的点中，计算与已标记visit点距离最小的点，标记visit,证明加入了最小生成树。
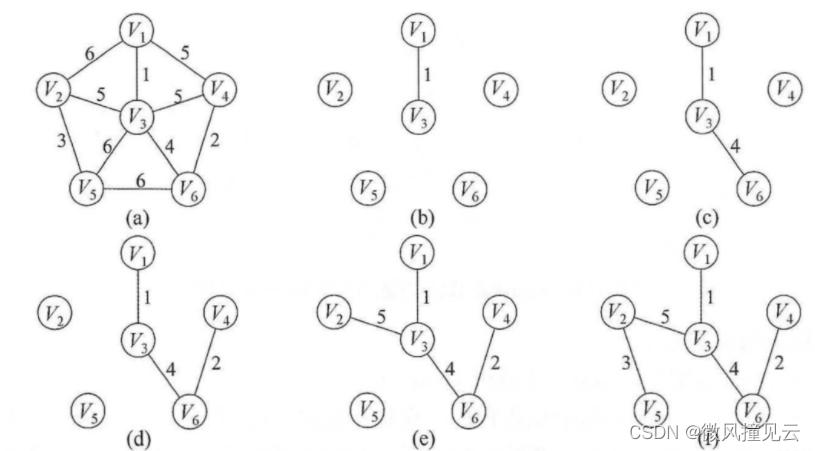
Kruskal
Kruskal是另一个计算最小生成树的算法，其算法原理如下。首先，将每个顶点放入其自身的数据集合中。然后，按照权值的升序来选择边。当选择每条边时，判断定义边的顶点是否在不同的数据集中。如果是，将此边插入最小生成树的集合中，同时，将集合中包含每个顶点的联合体取出，如果不是，就移动到下一条边。重复这个过程直到所有的边都探查过。
第1步：将边<E,F>加入R中。
边<E,F>的权值最小，因此将它加入到最小生成树结果R中。
第2步：将边<C,D>加入R中。
上一步操作之后，边<C,D>的权值最小，因此将它加入到最小生成树结果R中。
第3步：将边<D,E>加入R中。
上一步操作之后，边<D,E>的权值最小，因此将它加入到最小生成树结果R中。
第4步：将边<B,F>加入R中。
上一步操作之后，边<C,E>的权值最小，但<C,E>会和已有的边构成回路；因此，跳过边<C,E>。同理，跳过边<C,F>。将边<B,F>加入到最小生成树结果R中。
第5步：将边<E,G>加入R中。
上一步操作之后，边<E,G>的权值最小，因此将它加入到最小生成树结果R中。
第6步：将边<A,B>加入R中。
上一步操作之后，边<F,G>的权值最小，但<F,G>会和已有的边构成回路；因此，跳过边<F,G>。同理，跳过边<B,C>。将边<A,B>加入到最小生成树结果R中。
修路问题1——题目描述
输入示例：
5 6
1 2 2
1 3 7
1 4 6
2 3 1
3 4 3
3 5 2
输出
8
Kruskal（过了100%）
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
/**
* Created with IntelliJ IDEA.
*
* @Auther: LiangXinRui
* @Date: 2023/3/3 9:07
* @Description: Kruskal算法在找最小生成树结点之前，需要对权重从小到大进行排序。
* 将排序好的权重边依次加入到最小生成树中（如果加入时产生回路就跳过这条边，加入下一条边），
* 当所有的结点都加入到最小生成树中后，就找到了这个连通图的最小生成树～
*/
public class demo83_kruskal_修建公路 {
static final int N = 300005;
static int n,m,count;
static long sum;
static Edge[] edges = new Edge[N];
static int[] pre = new int[N];
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static int find(int v) {
if (v != pre[v]) {
pre[v] = find(pre[v]);
}
return pre[v];
}
public static void main(String[] args) throws Exception {
String[] s = br.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
for (int i = 1; i <= n; i++) {
pre[i] = i;
}
for (int i = 0; i < m; i++) {
String[] s1 = br.readLine().split(" ");
int a, b, c;
a = Integer.parseInt(s1[0]);
b = Integer.parseInt(s1[1]);
c = Integer.parseInt(s1[2]);
edges[i] = new Edge(a, b, c);
}
Arrays.sort(edges, 0, m);
for (int i = 0; i < m; i++) {
int a = edges[i].a;
int b = edges[i].b;
int w = edges[i].w;
a = find(a);
b = find(b);
if (a != b) {//这里不能写成 if (find(a) != find(b))
pre[a] = b;
sum += w;
count++;
}
}
if (count == n - 1) {
System.out.println(sum);
} else {
System.out.println(-1);
}
}
static class Edge implements Comparable<Edge> {
int a;
int b;
int w;
Edge(int a, int b, int w) {
this.a = a;
this.b = b;
this.w = w;
}
public int compareTo(Edge e) {
return w - e.w;
}
}
}
堆优化的prim（过了60%，有可能哪儿写错了？）
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
/**
* @Author: LiangXinRui
* @Date: 2023/03/02/20:16
* @Description:
*/
public class demo83_prim_堆优化 {
static int[] head, next, ends, pre;
static int n, m, num, total, begin;
static double sum;
static double[] weights, dis;
static boolean[] vis;
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static class pair {
double first;//记录 边权
int second;//记录 下一个结点
public pair() {
}
public pair(double first, int second) {
this.first = first;
this.second = second;
}
}
//自定义比较类，升序排列
static Comparator<pair> comparator = (o1, o2) -> o1.first - o2.first > 0 ? 1 : 0;
static Queue<pair> queue = new PriorityQueue<>(comparator);
static void add(int start, int end, int weight) {
ends[total] = end;
weights[total] = weight;
next[total] = head[start];
head[start] = total;
total++;
}
static void prim() {
queue.offer(new pair(weights[0], ends[0]));
vis[begin] = true;
while (!queue.isEmpty() && num < n) {
double len = queue.peek().first;
int to = queue.peek().second;
queue.poll();
if (!vis[to]) {
sum += len;
num++;// 找到一条边
vis[to] = true;// 标记一下，表示我这条边已经用过
for (int i = head[to]; i != -1; i = next[i]) {
if (weights[i] < dis[ends[i]]) {// 如果当前边权小，更新
dis[ends[i]] = weights[i];
queue.offer(new pair(weights[i], ends[i]));// 把新的边权和结点加入队列
}
}
}
}
}
public static void main(String[] args) throws IOException {
String[] firstStr = br.readLine().split(" ");
n = Integer.parseInt(firstStr[0]);
m = Integer.parseInt(firstStr[1]);
dis = new double[n + 1];
head = new int[2 * m + 1];//表示以 i 为起点的最后一条边的编号
next = new int[2 * m + 1];//存储与当前边起点相同的上一条边的编号
ends = new int[2 * m + 1];//存储边的终点
weights = new double[2 * m + 1];//存储边的权值
vis = new boolean[2 * m + 1];
Arrays.fill(head, -1);//初始化
for (int i = 1; i <= n; i++) {
dis[i] = Double.MAX_VALUE / 2;
}
for (int i = 0; i < m; i++) {
String[] secondStr = br.readLine().split(" ");
int start = Integer.parseInt(secondStr[0]);
if (i == 0) begin = start;
int end = Integer.parseInt(secondStr[1]);
int weight = Integer.parseInt(secondStr[2]);
add(start, end, weight);
add(end, start, weight);
}
prim();
if (n - 1 == num) {
System.out.printf("%.0f", sum);
} else {
System.out.println("-1");
}
}
}
总结
遇到困难时首先想到的不应该是退缩，而是探索！
文章粗浅，希望对大家有帮助！
参考博客：
【最小生成树】Prim算法和Kruskal算法的区别对比
Prim算法（java）
克鲁斯卡尔算法（Kruskal）详解
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
