代码随想录day37完全背包

动态规划 part05

完全背包

视频讲解：带你学透完全背包问题！ 和 01背包有什么差别？遍历顺序上有什么讲究？_哔哩哔哩_bilibili

https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html 

完全背包:

n个物品，任选且每个物品都可以取无数次

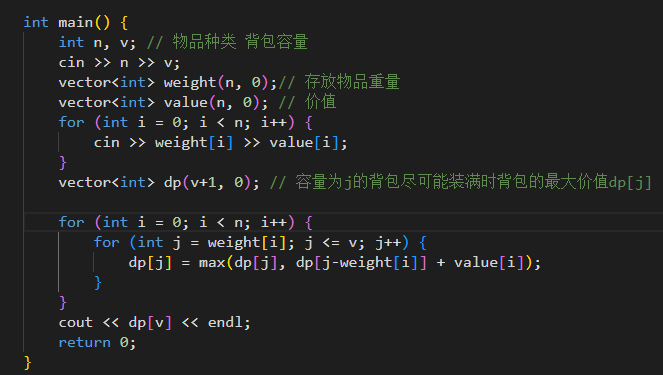
无论是01背包还是完全背包总结来说就是在所有塞满背包的方式中找出一种方式使背包的价值最大，那么当我们可以放物品i；

1. 不放物品i，用物品0到i-1，任选物品使背包j价值最大dp[i-1][j]
2. 上述情况下背包已经满了那考虑放i的情况，就需要先把i的位置容量预留出来j-weight[i],当然预留出来容量的背包价值也要最大dp[i-1][j-weight[i]],再放入物品i，则背包j被装满的价值dp[i-1][j-weight] + value[i];

上述两种情况都是装满背包的方式，我们的目的就是再背包被装满的情况下，使价值最大，显然dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight] + value[i])

和完全背包不同的是当我们可以重复放同一个物品时，在上述两种情况的前提下这就是三种方式，这种方式是通过更新背包的顺序来处理的：

这时候要考虑到状态转移的方向了，我们总是由前一层的状态推导到当前层的状态，当背包容量足够大物品的数目和总重量不够，在01背包中我们背包价值最大的状态背包的重量可能远远小于背包的最大容量，在完全背包中，物品可以重复装，所以：

1. 无论背包容量多大，保证价值最大的情况下尽可能装满，这就要求每当可以放入新物品我们都要先更新前面的背包价值，
2. 在1的条件下，推导出可以放物品i时的背包价值

总的来说，每个背包（容量由小到大）的价值不是由上一层状态转移来，而是同一层，容量较小的背包的状态转移来

所以，遍历顺序可以颠倒，因为状态和上一层没关系，只要当前层前面的状态更新了就可以（纯完全背包），这里的层是指可以放的物品到哪一个了。

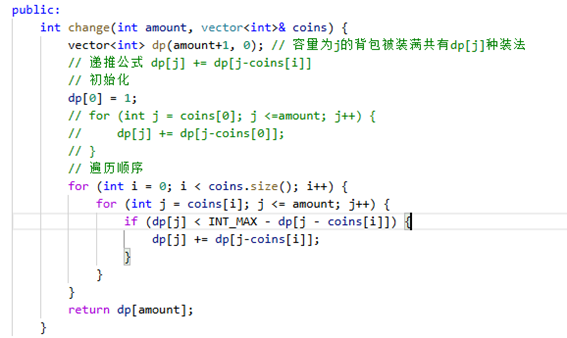
518. 零钱兑换 II

视频讲解：动态规划之完全背包，装满背包有多少种方法？组合与排列有讲究！| LeetCode：518.零钱兑换II_哔哩哔哩_bilibili

代码随想录  

转化：

硬币面额：重量

硬币面额：价值

总金额：背包容量

问：由多少种方式可以装满背包，组合结果不重复

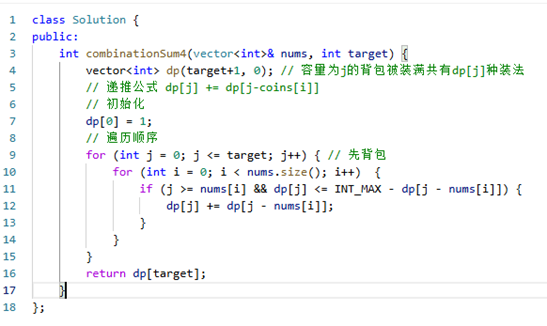
377. 组合总和 Ⅳ

视频讲解：动态规划之完全背包，装满背包有几种方法？求排列数？| LeetCode：377.组合总和IV_哔哩哔哩_bilibili

代码随想录

零钱兑换II：排列问题先背包后物品，要从递推的过程去理解 为什么先遍历背包

上图截自代码随想录公众号

dp[4] = dp[4-nums[0]] + dp[4-nums[1]] + dp[4-nums[2];

同理 dp[3] = dp[3-nums[0]] + dp[3 – nums[1]] +dp[3 -nums[2];

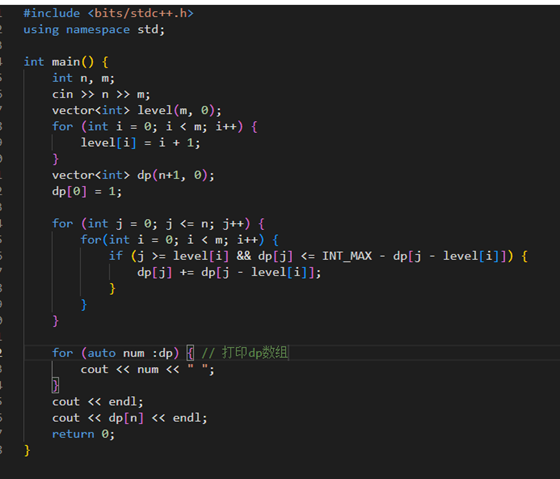
70. 爬楼梯 （进阶）

代码随想录