利用控制方法求解优化问题（李雅普诺夫方法）介绍及matlab实现

---

前言

参考文献：[1]张瑞友,王超慧,陈勇强.基于控制思想求解非线性规划问题的李雅普诺夫方法[J].东北大学学报(自然科学版),2021,42(09):1217-1225+1245.
文章中指出约束非线性规划问题广泛存在于智能制造领域，多年来一直是学术界的研究热点与难点之一，解决这类问题的方法主要有牛顿迭代法等启发式方法及各种智能优化方法( 或称为元启发式算法)。 这些智能优化方法通常计算时间较长且难以保证收敛。

一、李雅普诺夫方法

1.李雅普诺夫方法的基本思想

李雅普诺夫方法具较强的处理约束能力和收敛性。李雅普诺夫方法将约束优化问题描述为一个动态系统，进而基于动态系统的稳定控制状态实现对优化问题的求解。

2.李雅普诺夫方法的具体求解过程

文章中介绍的李雅普诺夫方法求解非线性规划问题的基本过程如下所示
任意给出下面形式的单目标非线性优化问题（P1）:

其中: x 为决策变量; f 为目标函数; g( x) 为n 维等式约束; h( x) 为m 维不等式约束，hmin和hmax分别为不等式约束的下界和上界。

引入非负松弛变量q( ≥0) ，将目标函数(1)的最小化转化为如下偏差函数的零点问题．

类似地，引入非负松弛变量s( ≥0)和t( ≥0) ，问题P1 的约束条件( 2) 和( 3) 可以转化为如下的零点问题

则：

求解式( 10) 的最小化问题，也就是求解如下方程:

由于问题的非线性特性，式( 11) 难以直接求解，设计1 个动态系统，其中的决策变量和松弛变量与时间相关． 在此假设下，可将式( 10) 视为李雅普诺夫函数． 根据李雅普诺夫定理［13］可知: 若能使式( 10) 的时间导数为负定或半负定，则该动态系统可以稳定收敛于平衡点．W( z) 对时间的求导结果为

上述为李雅普诺夫方法得到渐进稳定系统的证明及推导，则根据上述分析，具体求解时采取如下方法：

3.思考

对于文章中介绍的方法，笔者认为该方法具有如下的局限性（仅供参考）：首先，如式(15)-(18)所示，该方法需要求多次偏导数，但是偏导数的求解过程需要耗费大量时间，当决策变量变多或约束条件及目标函数较为复杂时可能不再适用（文章中的案例目标函数和约束条件比较简单，决策变量也比较少）。其次，该方法求解结果严重依赖于目标函数的松弛变量q和初始值的选取，以及目标函数和松弛变量q的变化速度（详情参见文章），但是这些都需要人为提前设定，当设定不合理时结果不好。

二、matlab实现

代码如下：

%没有约束情况下的非线性规划问题求解
%min f(x1,x2)=(6*x1/(2+x1^2+x2^2))
%% 定义初始条件
x1 = 2;    % 初始值
x2 = 2;    % 初始值
q0 = -10;
initialConditions = [x1; x2; q0];
kq=1e3;
kx=1e5;
n=size(initialConditions,1);%方程个数
%% 定义时间范围
tspan = [0, 0.01]; % 仿真时间范围
%% 定义目标函数
%定义决策变量
for i=1:1:n
    x(i)=sym (['x',num2str(i)]); 
end
%定义目标函数
% f=(6*max(x(1),x(2))/(2+(x(1))^2+(x(2))^2));
f=(6*x(1)/(2+(x(1))^2+(x(2))^2));
%% 构建微分方程组
%取目标函数偏导
% f_diff=zeros(2,0);
for i=1:1:n-1
    f_diff(i)=diff(f,x(i));
end
%构建决策变量的微分方程组
for i=1:1:n-1
    f_ob(i)=-kx*(f_diff(i)*(f-x(n)));
end
% 构建目标函数中松弛变量的微分方程
f_ob(n)=kq*(f-x(n));
% 将符号函数转换为函数句柄
expr=f_ob';
f_obfh = matlabFunction(expr, 'Vars', {x});
% 定义ODE函数
odeFunc = @(t, y) [
    f_obfh(y.');
];
%% 使用ode45求解器进行求解
[t, sol] = ode45(odeFunc, tspan, initialConditions);
sol(:,end+1)=sol(end,n)-sol(:,end);
figure;
plot(t, sol);
xlabel('时间');
ylabel('状态变量');

legend('x1','x2','f','error');
x=sol(end,1:n);

得到如下结果：

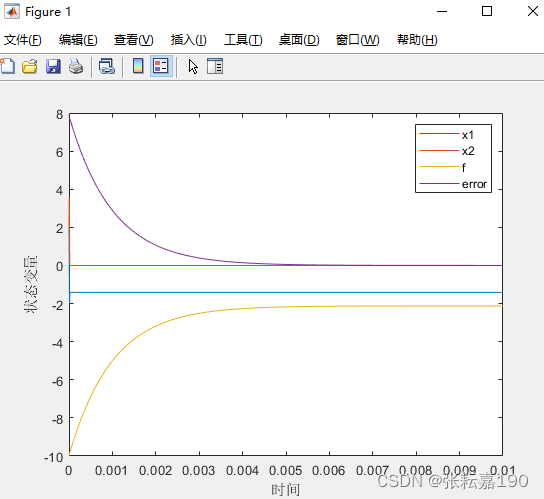
与直接求解最小值x1=-1.414,x2=0得到的结果相同。
但是，当参数选取不合理（如下）时，得到的结果不正确

%没有约束情况下的非线性规划问题求解
%min f(x1,x2)=(6*x1/(2+x1^2+x2^2))
%% 定义初始条件
x1 = 2;    % 初始值
x2 = 2;    % 初始值
q0 = -10;
initialConditions = [x1; x2; q0];
kq=1e5;
kx=1e5;
n=size(initialConditions,1);%方程个数
%% 定义时间范围
tspan = [0, 0.01]; % 仿真时间范围
%% 定义目标函数
%定义决策变量
for i=1:1:n
    x(i)=sym (['x',num2str(i)]); 
end
%定义目标函数
% f=(6*max(x(1),x(2))/(2+(x(1))^2+(x(2))^2));
f=(6*x(1)/(2+(x(1))^2+(x(2))^2));
%% 构建微分方程组
%取目标函数偏导
% f_diff=zeros(2,0);
for i=1:1:n-1
    f_diff(i)=diff(f,x(i));
end
%构建决策变量的微分方程组
for i=1:1:n-1
    f_ob(i)=-kx*(f_diff(i)*(f-x(n)));
end
% 构建目标函数中松弛变量的微分方程
f_ob(n)=kq*(f-x(n));
% 将符号函数转换为函数句柄
expr=f_ob';
f_obfh = matlabFunction(expr, 'Vars', {x});
% 定义ODE函数
odeFunc = @(t, y) [
    f_obfh(y.');
];
%% 使用ode45求解器进行求解
[t, sol] = ode45(odeFunc, tspan, initialConditions);
sol(:,end+1)=sol(end,n)-sol(:,end);
figure;
plot(t, sol);
xlabel('时间');
ylabel('状态变量');

legend('x1','x2','f','error');
x=sol(end,1:n);

这是由于此时选取的q的收敛速度过快（代码第八行），且q的初始值设置较小，目标函数尚未收敛到最小值即与q相等。如下图所示（具体参见文章解释）