小白从零开始学习“公钥密文传输”

1. 公钥密码通信

• 密钥分配问题

加密通信的核心本质就是对信息进行加密，防止信息被除了发送方与接收方之外的第三者获取。因此采用加密技术，这样即使第三者获得了加密后传输的信息，他也无法破译，无法得到真实原始的信息。但接收方目的也是要获得原始信息，想让接收方能够破解密码，发送方就要教会接收方怎么解密，这个过程一般体现为发送方把加密密钥也传输给接收方，接收双方采用同一个密钥进行加密或者解密操作，这种密码通常被称为对称密码。

此时新的问题--密钥分配问题即出现了，既然发送的加密信息有概率被第三方获取，那么传输的加密密钥也有概率被获取，此时的加密还是没有效果。

解决密码分配问题的一种解法就是公钥密码，也被称为非对称密码。

• 公钥密码与私钥密码

在上文所提到的公钥密码通信模式中，发送方和接收方所使用的密码是不同的，一组密码包含公钥和私钥这样一对密码。

公钥负责对信息进行加密，相当于给信息上了一把锁，这个公钥是公开的，所有人都知道的，第三者也可以获取，任何想给接受方发信息的人都可以用这个公钥密码对信息进行加密。

而私钥密码对信息进行解密，相当于解开信息上锁的钥匙，这个私钥是严格保密的，但是只需要接收方知道就可以了，不需要传输通信，因此避免了密钥传输问题。接收方获取了公钥加密的信息后，再用私钥进行破解，这样第三者即使截取了公钥加密的信息，没有私钥也徒劳无功。

• 公钥密码传输流程-Part1/无证书/无签名

此时我们考虑一个最简单的公钥密码传输过程：消息的接收方生成一对公钥与私钥，公钥发送给发送方，而私钥自己保留。此时的发送方将要传输的信息通过公钥进行加密，加密后的信息大胆的传输给接收方，而接收方根据手里的私钥对信息解密，这样就完成了一次需要加密的信息的传输。

上述的流程可以见下图。

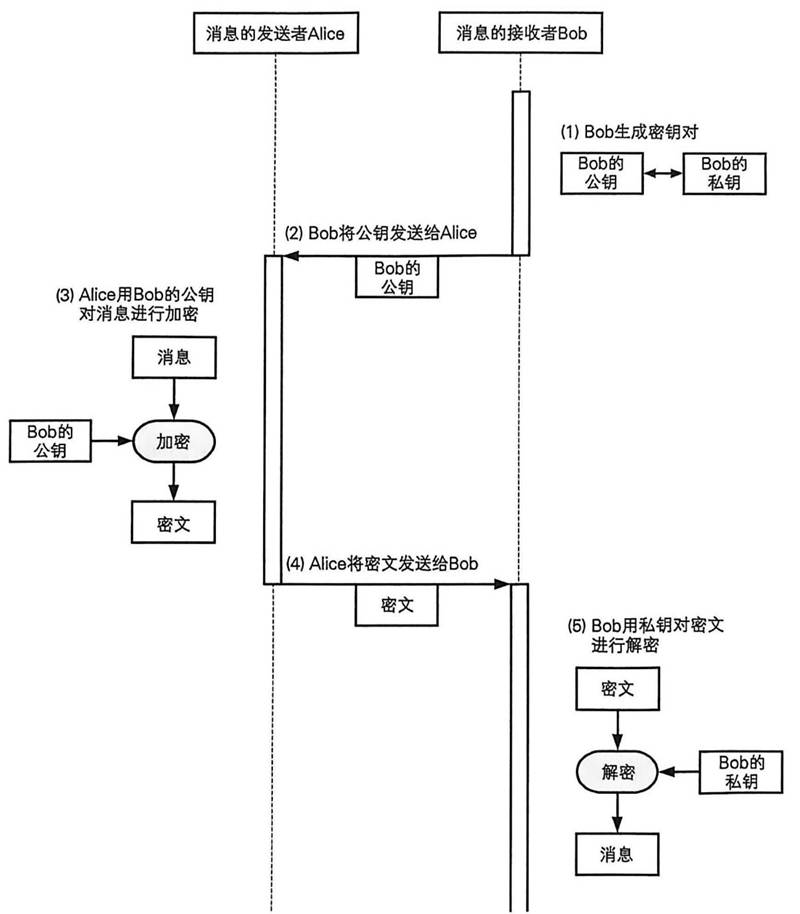
图1 简单的公钥密码传输过程

• 数字签名

上述讨论的公钥密码的简单通信基于一个事实：任何知道公钥密码的人都可以对信息进行加密，向接收方发送“加密信息”。此时我们考虑加密通信的应用场景：公司机密。财务往来……等等，试想你通过自己的私钥解密，发现有人用公钥加密了一段“借我2000元”的信息给你，署名是你的朋友，当你把钱转了过去，你的“朋友”缺矢口否认这件事，声称没有发过这样的消息，联想到“任何知道公钥密码的人都可以对信息进行加密，向接收方发送加密信息”这个事实。此时你没有任何办法防止他进行否认！

要解决“防止接收方否认”这个问题，最好的办法就是像借条一样让发送方签名、“摁手印”，有没有不能被仿制的手印呢？这就是“数字签名”，其本质就是把公钥密码进行反向应用。

刚刚的传输流程只提到了接收方的一对密钥，我们称之为Recv_PK（接收方公钥）和Recv_SK（接收方私钥），那么发送方可不可以也生成一对完全不同的密钥呢？答案肯定是可以的，我们称之为Send_PK（发送方公钥）和Send_SK（发送方私钥），通过这对发送方公钥私钥，就可以完成无法否认的数字签名，具体流程如下：

1. 在准备开始之前，发送方把Send_PK（发送方公钥）通知接收方，接收方把Recv_PK（接收方公钥）通知发送方。
2. 发送方准备好了写好的原始信息，作为要传输的密文，用Recv_PK（接收方公钥）进行加密，等待接收方用自己的私钥解开获取原始信息。此时得到了“加密消息”。
3. 发送方根据这段原始信息的部分特征，得到其散列值，将这个散列值作为签名的内容，用自己的私钥，也就是Send_SK（发送方私钥）进行加密，得到了“签名”。这一过程称为“对消息进行：‘数字签名’”。
4. 发送方将“加密消息+签名”一并传输给接收方

• 接收方根据自己的私钥，对加密消息进行解密，得到原始信息，并计算其接收消息散列值。
• 接收方根据发送方公钥，对签名进行反向解密（这一部分可参考钥匙和锁理论，你用钥匙插进锁里能打开锁，用锁也能反向验证钥匙的正确性）得到了原始签名，也就是发送时的散列值。
• 如果接收消息的散列值和签名里的散列值一模一样，那就可以认为，这个消息就是发送方发来了，并且中途没有被人修改

**此过程用到了单向散列函数的相关知识

• 公钥密码传输流程-Part2/无证书/含签名

数字签名应用了“没有私钥的人无法生成使用该私钥所生成的密文”这一核心原理，上述流程可见下图：

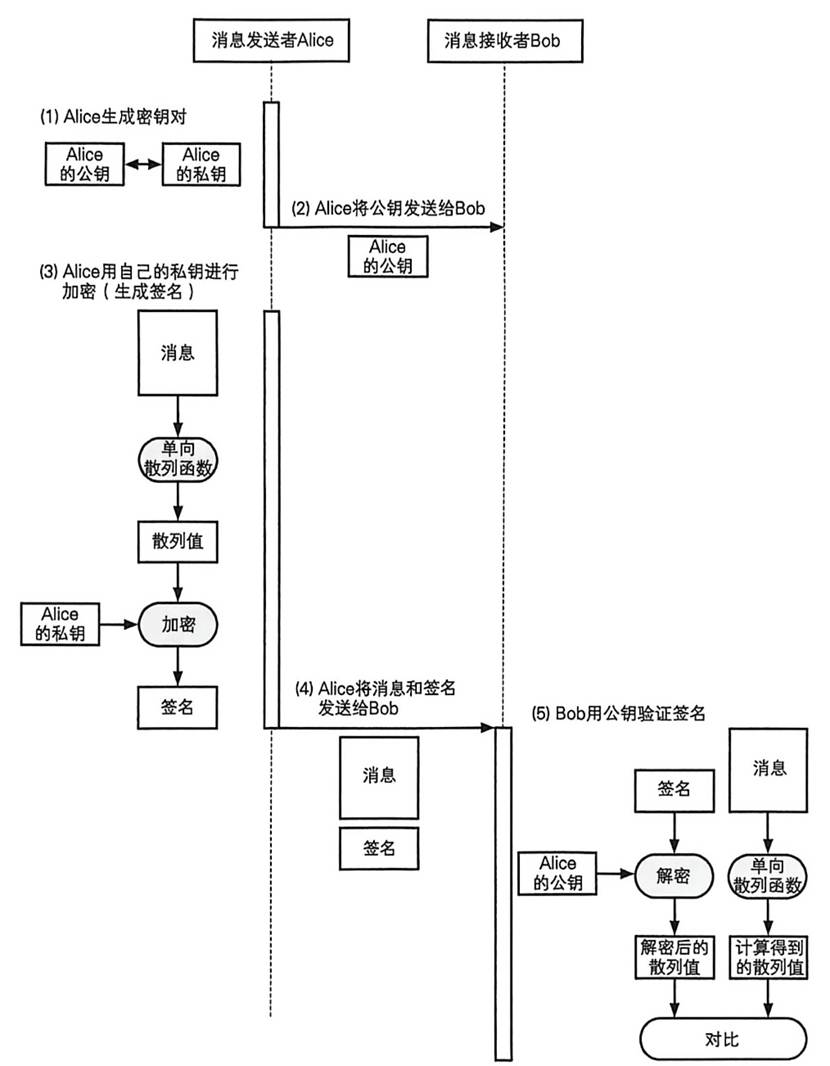
图2 含有数字签名的公钥密码传输过程

• 中间人攻击

那么这样的传输方案就完全避免了中间人获取原始信息的可能性了吗？答案当然是否定的，在上文的介绍中其实隐含了一次信息传输过程：当发送方想要给接收方传输信息时，他需要向接收方索要公钥，接收方把公钥发送给发送方。

这个过程中第三者是有机可乘的，这个第三者我们一般称为“中间人”，中间人接听到了发送方向接收方索要公钥的信息，并把接收方把公钥发送给发送方的通信进行拦截，转而将自己生成的一对非对称密码当中的公钥（伪接收方公钥）发给发送方，发送方毫无察觉，利用这个错误的公钥进行加密、发送，此时中间人再通过自己的私钥（伪接收方私钥）进行破解，就能拿到原始的传输信息了。

上述流程可以简化为下图所示：

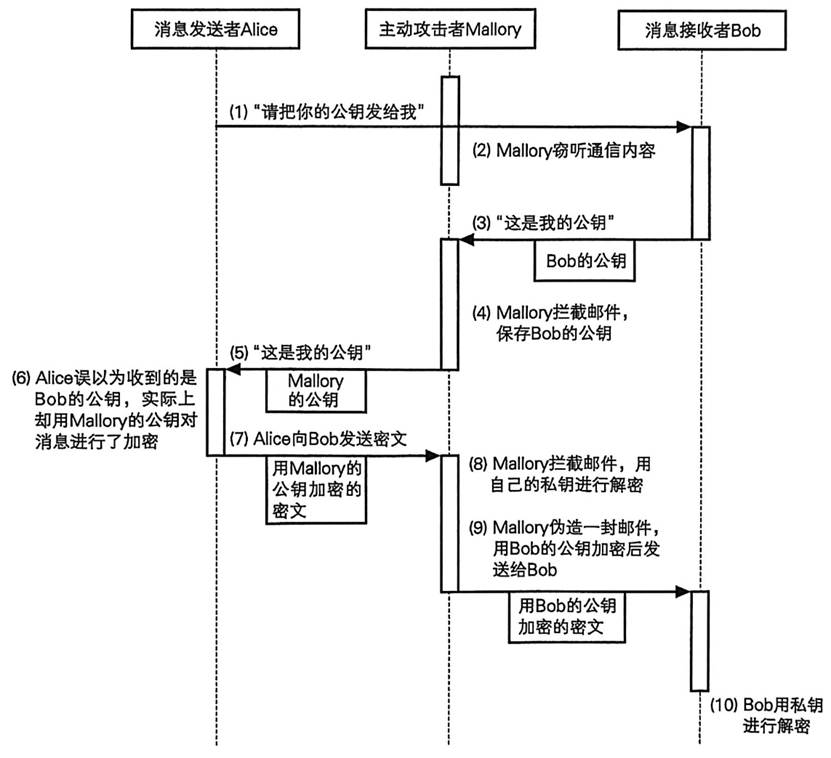
图3 被中间人攻击的公钥密码传输过程

那么我们会有这样的疑问：数字签名可以识别出中间人吗？答案是不能的，数字签名主要的作用是“防否认”并不能验证发出消息的到底是谁，只能让发出消息的这个人事后承认这个消息是他发的，但那于事无补。

更技术的理解，既然中间人可以截获信息，他完全可以把发送方传输给接收方的Send_PK（发送方公钥）截获，并换成自己的“伪发送方公钥”，并用自己的“伪发送方私钥”对消息散列值进行签名，接收方同样无法识别。

话说到这里似乎陷入了一个死循环，我们永远无法防备这个强大的“中间人”了吗？这里就需要引入一个绝对权威的第三方机构了！

• 认证机构&数字证书

其实通过上文的矛盾我们不难看出，无法防范的根本原因是：“我无法证明向我发消息的这个人就是我想要的接收方”，其引申含义就是“我无法确定我拿到的这个公钥就是接收方的公钥”。

这个问题看似无解，但是联系到现实生活，你该如何证明你的电动车是你的呢？无论你怎么说电动车是你的，我都说你是伪造的，就是不认可你，这时候你怎么办？很多人就会想到，我给你看公安局的驾驶证！你敢质疑公安局吗？这样便完成了绝杀，是基于“公安局”这样的权威第三方机构的信誉和地位完成的。

那么在密文传输过程中，假设有一个公安局一样的第三方权威机构，他就能告诉你：“你收到这个公钥，就是属于接收方的！百分百没错！”或者“你收到这个公钥，就是属于发送方的！百分百没错！”那么中间人不攻自破，因为小偷是无法拿到公安局认证的。这个机构就是“认证中心”。

继续思考，只要有一个接收方一个发送方，就会有一对密钥，甚至密钥还可以不定期更换，每发送一次消息就要让认证中心认证一次，认证中心且不是忙不过来？那有没有什么办法让认证中心不出手，又能证明你的公钥正确性呢？

聪明的朋友很快就想到了，认证中心也可以有自己的非对称密钥对，也就是Trent_PK（认证中心公钥）和Trent_SK（认证中心私钥），此时我们默认Trent_PK（认证中心公钥）是所有人都已知的！并且Trent_SK（认证中心私钥）是完全安全不会被中间人模仿的（警察局的保险箱绝对安全）。那么，如果让认证中心对发送接收双方互换的密钥进行签名，双方收到后认证来自认证中心的数字签名，这个数字签名完全正确，就能证明随签名而来的消息（密钥）是完全正确的！这个利用Trent_SK（认证中心私钥）对消息进行数字签名的过程，就叫做“开具数字证书”，这个认证中心私钥生成的数字签名，就是“数字证书”。

那么有了认证中心的参与，我们的传输过程会变成怎么样呢？在发送方和接收方交互消息之前，要发生以下动作：

1. 接收方把自己的公钥和相关信息（邮箱，姓名等等）通过线下等方式安全的交给认证中心，认证中心基于接收方公钥和相关信息的散列值，用认证中心私钥进行加密，生成数字签名，开具数字证书。
2. 接收方把这个数字证书发给发送方，发送方百度一下得到了人尽皆知的认证中心公钥，利用这个公钥解密得到数字签名的原始信息（接收方公钥散列值），并把一并收到的接收方公钥信息也计算一个散列值，两个数值一对比，perfect！完全一样！那么说明这个接收方公钥就是接收方发来的，且没有被修改过，完全正确。

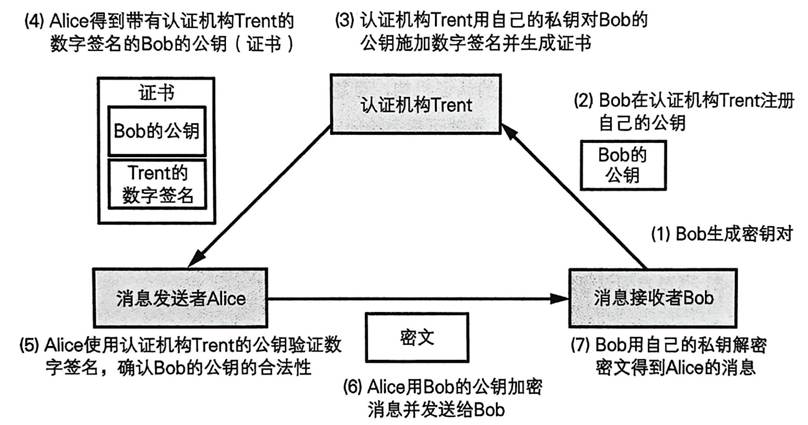
图4 认证中心签发接收者公钥证书的过程

--小插曲：如果我是一个不怀好意的第三方，我拿着一个真的数字证书来骗你信息怎么办？这时候就代表开具的数字证书不仅仅要包含接收方公钥了，还要有相关信息，一旦相关信息对不上，散列值就也对不上，此时如果对上了验证成功，那么这个公钥就一定是相关信息里接收方的那个公钥！

1. 发送方同理，把自己的信息和发送方公钥发给认证中心，将数字证书发给接收方，接收方通过认证。
2. 此时！发送方有了完全可靠的接收方公钥，能够放心的把要传输的密文信息用这个接收方公钥进行加密，同时用自己的发送方私钥对散列值加密完成签名。而接收方有了完全可靠的发送方公钥，通过公钥对签名解析得到可靠的签名数值，也能用自己的私钥对加密信息进行解密，获得加密信息的散列值数值，两者对比无误，即完成了一次可靠的公钥密文传输。