AAAI2022 | AI-FGTM | 使对抗样本更具迁移性和难以区分性

---

论文链接

本文 “Making Adversarial Examples More Transferable and Indistinguishable” 提出 Adam 迭代快速梯度双曲正切方法（AI-FGTM），通过改进梯度处理步骤，生成迁移性和不可区分性更好的对抗样本，在多种攻击场景下优于现有方法，提升攻击成功率的同时降低平均扰动。

---

摘要-Abstract

Fast gradient sign attack series are popular methods that are used to generate adversarial examples. However, most of the approaches based on fast gradient sign attack series cannot balance the indistinguishability and transferability due to the limitations of the basic sign structure. To address this problem, we propose a method, called Adam Iterative Fast Gradient Tanh Method (AI-FGTM), to generate indistinguishable adversarial examples with high transferability. Besides, smaller kernels and dynamic step size are also applied to generate adversarial examples for further increasing the attack success rates. Extensive experiments on an ImageNetcompatible dataset show that our method generates more indistinguishable adversarial examples and achieves higher attack success rates without extra running time and resource. Our best transfer-based attack NI-TI-DI-AITM can fool six classic defense models with an average success rate of 89.3% and three advanced defense models with an average success rate of 82.7%, which are higher than the state-of-theart gradient-based attacks. Additionally, our method can also reduce nearly 20% mean perturbation. We expect that our method will serve as a new baseline for generating adversarial examples with better transferability and indistinguishability.

快速梯度符号攻击系列是用于生成对抗样本的常用方法。然而，由于基本符号结构的限制，大多数基于快速梯度符号攻击系列的方法无法平衡不可区分性和迁移性。为了解决这个问题，我们提出了一种名为Adam迭代快速梯度双曲正切方法（AI - FGTM）的方法，用于生成具有高迁移性且难以区分的对抗样本。此外，还采用了更小的内核和动态步长来生成对抗样本，以进一步提高攻击成功率。在与ImageNet兼容的数据集上进行的大量实验表明，我们的方法能够生成更难以区分的对抗样本，并且在不增加运行时间和资源的情况下实现更高的攻击成功率。我们性能最佳的基于迁移的攻击方法NI - TI - DI - AITM能够以89.3%的平均成功率欺骗六个经典防御模型，以82.7%的平均成功率欺骗三个先进防御模型，这比最先进的基于梯度的攻击方法表现更优。此外，我们的方法还可以将平均扰动降低近20%。我们期望我们的方法能成为生成具有更好迁移性和不可区分性的对抗样本的新基线。

---

引言-Introduction

该部分主要介绍了研究背景、问题以及提出的方法和贡献，具体内容如下：

1. 研究背景：深度神经网络（DNNs）在诸多任务中取得成功，但易受对抗样本攻击，即微小扰动的输入会使DNNs产生错误结果，且对抗样本具有迁移性，对现实应用构成严重威胁，引发了大量防御方法的研究。攻击方法大致分为基于梯度的方法、基于分数的方法和基于决策的方法，本文聚焦于基于梯度的方法。
2. 存在问题：基于梯度的方法生成的对抗样本虽满足 $L_p$ 约束且黑盒成功率较高，但易被识别。基于基本符号结构的方法存在局限性，如TI - MI - FGSM中梯度处理步骤会破坏梯度信息，符号函数还会增大扰动规模 。
3. 提出方法：提出Adam迭代快速梯度双曲正切方法（AI - FGTM），通过改进主要梯度处理步骤，提高对抗样本的不可区分性和迁移性。以TI - MI - FGSM为例，用Adam和tanh函数分别替代动量算法和符号函数，采用动态步长和更小的高斯模糊滤波器。
4. 研究贡献：改进主要梯度处理步骤，提升对抗样本的不可区分性和迁移性；与现有基于迁移的攻击方法结合，能获得更小的扰动和更大的损失；实验证明，在不增加运行时间和资源的情况下，攻击成功率高于当前最先进的基于梯度的攻击方法。

图1：我们方法的概述。
( a ) 我们用双曲正切函数（tanh函数）代替符号函数，以生成更小的扰动。
( b ) 我们使用Adam优化器，而非动量法和梯度归一化，仅在十次迭代中就能获得更大的损失值。
( c ) 我们在高斯模糊中使用更小的内核，以避免梯度信息的损失。
( d ) 我们逐渐增大步长。

图2：干净样本与由三种组合攻击生成的对抗样本的对比。（1）TI-DI-AITM（$\lambda =0.65$）实现了与TI-DIM相似的成功率，并且生成了更难以区分的对抗样本。（2）TI-DI-AITM（$\lambda =1.3$）比TI-DIM实现了高得多的成功率，并且生成了更难以区分的对抗样本。

---

现有攻击方法回顾-Review Of Existing Attack Methods

该部分主要回顾了基于梯度的攻击方法，先给出问题定义，再详细介绍各类方法，具体内容如下：

1. 问题定义：给定一组预训练分类器，包括白盒分类器 $(f_{Wi}{)}_{i\in [N]}$ 和未知分类器 $(f_{Bj}{)}_{j\in [M]}$，以及干净样本 $x$，其能被正确分类为真实标签 $y^{true}$。目标是利用白盒分类器生成满足 ${\Vert x^{adv}-x\Vert }_p\le \epsilon$ 的对抗样本 $x^{adv}$，本文聚焦 $p=\infty$ 的非针对性攻击，且对抗样本要能同时误导白盒和未知分类器。
2. 基于梯度的方法
   • 快速梯度符号法（FGSM）：建立基于梯度方法的基本框架，通过一步更新，最大化给定分类器的损失函数 $J(x^{adv},y^{true})$ 来生成对抗样本，公式为 $x^{adv}=x+\epsilon \cdot sign\left({\nabla }_{x}J\left(x,y^{true}\right)\right)$ 。
   • 基本迭代法（BIM）：FGSM的迭代版本，在白盒攻击中表现较好，但在基于迁移的攻击中效果欠佳，通过小步长 $\alpha$ 迭代更新对抗样本 。
   • 动量迭代快速梯度符号法（MIFGSM）：通过在梯度计算中引入动量项来增强对抗样本的迁移性。
   • Nesterov迭代法（NIM）：在MIFGSM基础上集成预期更新，进一步提高对抗样本的迁移性。
   • 尺度不变法（SIM）：应用输入图像的尺度副本提升迁移性，但运行时间和资源需求大。
   • 多样输入法（DIM）：每次迭代以概率 $p$ 对对抗样本进行随机缩放和填充，可与其他基于梯度的方法结合提升迁移性。
   • 平移不变法（TIM）：通过一组平移示例优化对抗样本，计算梯度时使用预定义高斯滤波器卷积。在有限资源下，NIM、TIM和DIM的组合（NI-TI-DIM）是目前较强的基于迁移的攻击方法。

---

方法-Methodology

该部分主要阐述了提出AI-FGTM方法的动机、AI-FGTM的具体内容以及它与NIM的结合方式，具体如下：

1. 动机
   • 符号函数的弊端：基于梯度的方法中符号函数存在缺陷，它将所有梯度值归一化到1、-1或0，导致梯度信息丢失，还会把小梯度值归一化到1或 -1，增加扰动大小。而tanh函数不仅能像符号函数那样归一化大梯度值，还能像 $y=x$ 函数那样保留小梯度值，可替代符号函数并减小扰动。
   • Adam优化器的优势：在对抗攻击中应用Nesterov加速梯度（NAG）和动量算法时发现，可迁移其他方法生成对抗样本。Adam优化器在少量迭代（$T=10$）中，比动量算法能获得更大损失，且能以 $m_t/\sqrt{v_t+\delta }$ 归一化梯度，因此可引入Adam优化器。
   • 动态步长的作用：传统收敛算法通过学习率衰减提升模型性能，现有基于梯度的方法设置稳定步长 $\alpha =\epsilon /T$。考虑到攻击方法旨在最大化目标模型损失函数，采用动态步长且 ${\sum }_{t=0}^{T-1}{\alpha }_t=\epsilon$，有望提高对抗样本迁移性。
   • 小内核高斯模糊的好处：大内核高斯模糊虽能提升对抗样本迁移性，但会导致梯度信息丢失。使用小内核高斯模糊可避免此问题，使梯度信息在生成对抗样本中发挥更重要作用。
2. AI-FGTM
   • Adam算法的应用与修改：Adam算法利用过去梯度平方的指数移动平均值来缓解学习率快速衰减。在对抗攻击中应用时，对其进行修改。初始设置 $x_0^{adv}=x$，$m_0=0$，$v_0=0$，计算第一和第二时刻估计值，公式分别为 $m_{t+1}=m_t+{\mu }_1\cdot {\nabla }_{x_t^{adv}}J\left(x_t^{adv},y^{true}\right)$ 和 $v_{t+1}=v_t+{\mu }_2\cdot {\left({\nabla }_{x_t^{adv}}J\left(x_t^{adv},y^{true}\right)\right)}^2$ 。
   • 更新对抗样本：用tanh函数替代符号函数更新对抗样本，步长 ${\alpha }_t$ 为动态变化，且满足 ${\sum }_{t=0}^{T-1}{\alpha }_t=\epsilon$，更新公式为 $x_{t+1}^{adv}=Cli{p}_{\epsilon }^x\left\{x_t^{adv}+{\alpha }_t\cdot tanh\left(\lambda \frac{m_{t+1}}{\sqrt{v_{t+1}}+\delta }\right)\right\}$ ，tanh函数可在不降低成功率的情况下减少对抗样本扰动。
3. AI-FGTM与NIM的结合：受NIM将预期更新集成到MI-FGSM的启发，将预期更新集成到AI-FGTM中。先按公式计算每次迭代步长，Nesterov项表示为 $x_t^{nes}=x_t^{adv}+{\alpha }_t\cdot \frac{m_t}{\sqrt{v_t}+\delta }$ ，后续更新步骤与AI-FGTM类似，最终将AI-FGTM、NIM、TIM和DIM的组合总结为NI-TI-DI-AITM，详细过程以算法形式给出。

---

实验-Experiments

该部分通过多种实验，验证了AI-FGTM方法的有效性，具体内容如下：

1. 实验设置
   • 数据集：使用NIPS 2017对抗竞赛中的1000张图像进行实验。
   • 模型：采用13个模型，包括4个非防御模型（如Inception v3、Inception v4等）用于制作对抗样本，6个经典防御模型（如Inc-v3ens3、Inc-v3ens4等）和3个先进防御模型（Feature Distillation、Comdefend、Randomized Smoothing ）用于评估对抗样本效果。
   • 基线：重点对比TI-DIM、NI-TI-DIM、TI-DI-AITM和NI-TI-DI-AITM，其中TI-DIM和NI-TI-DIM是当前先进方法。
   • 超参数：依据相关方法，设置最大扰动 $\epsilon =16$，迭代次数 $T=10$。TI-DI-AITM中内核大小设为 $9\times 9$，其他对比方法设为 $15\times 15$。
   • 平均扰动大小计算：对于大小为 $M\times N\times 3$ 的对抗样本 $x^{adv}$，平均扰动大小 $P_m=\frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{\sum }_{k=1}^3|x_{ijk}^{adv}-x_{ijk}|}{M\times N\times 3}$。
2. 运行效率比较：使用Nvidia GPU GTX 1080 Ti比较各攻击方法运行时间。结果显示，结合AI-FGTM的攻击方法未增加运行时间，而SIM在单模型和模型集成设置下运行时间长且资源需求大，后续实验将其排除。
   
   表1：本文中使用的缩写
   
   表2：为Inception v3、Inception v4、Inception ResNet v2、ResNet v2 - 101以及这四个模型的集成生成1000个对抗样本所需的运行时间（秒）。
3. 消融研究：对比不同部分对方法的影响，观察到tanh函数和Adam都能减小扰动大小，且Adam可提升对抗样本迁移性；二者结合能大幅减小扰动，但对迁移性提升有限；较小内核和动态步长虽使扰动稍有增加，但能提高对抗样本迁移性。
   
   表3：对tanh函数、Adam优化器、内核大小和动态步长效果的消融研究。使用TI-DIM以及结合了我们方法不同部分的TI-DIM，分别为Inception v3、Inception v4、Inception ResNet v2、ResNet v2-101生成对抗样本。我们比较了生成的对抗样本针对六个经典防御模型的平均扰动和平均攻击成功率。
4. 单模型攻击场景验证：比较基于AI-FGTM的攻击方法和基线攻击对六个经典防御模型的成功率。结果表明，基于AI-FGTM的攻击方法始终大幅优于基线攻击，生成的对抗样本迁移性和不可区分性更好。
   
   表4：在单模型设置下，针对六个防御模型的对抗攻击成功率（%）。对抗样本分别使用TI-DIM、NI-TI-DIM、TI-DI-AITM和NI-TI-DI-AITM为Inception v3、Inception v4、Inception ResNet v2、ResNet v2-101生成。
5. 模型集成攻击场景验证：展示针对四个非防御模型集成生成的对抗样本的成功率。结果显示，本文方法对经典防御模型和先进防御模型的攻击成功率更高。如NI-TI-DI-AITM对六个经典防御模型平均成功率达89.3%，对三个先进防御模型平均成功率达82.7%，体现出方法的优越性。
   
   图3：使用不同攻击方法为Inception v3、Inception v4、Inception ResNet v2和ResNet v2 - 101的集成模型生成的对抗样本结果。
   
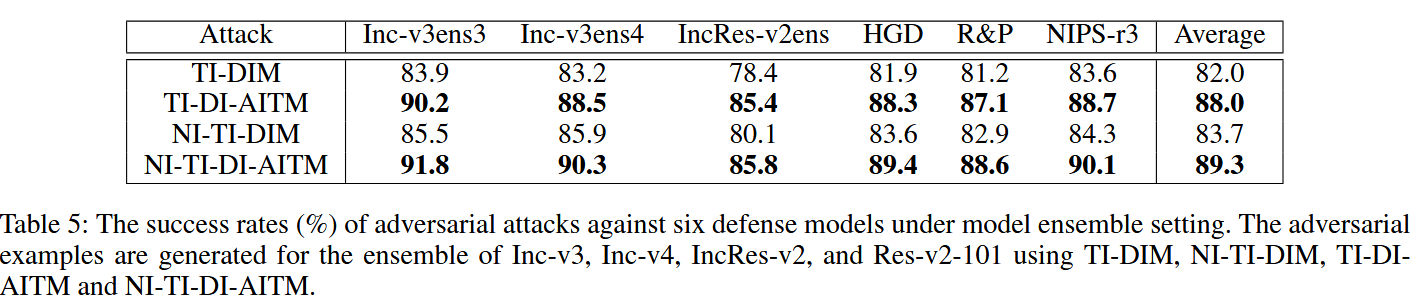
   表5：在模型集成设置下，针对六个防御模型的对抗攻击成功率（%）。这些对抗样本是使用TI-DIM、NI-TI-DIM、TI-DI-AITM和NI-TI-DI-AITM，针对Inception v3、Inception v4、Inception ResNet v2和ResNet v2-101的模型集成生成的。
   
   表6：在模型集成设置下，针对特征蒸馏（Feature Distillation）、Comdefend和随机平滑（Randomized Smoothing）的对抗攻击成功率（%）。对抗样本是使用TI-DIM、NI-TI-DIM、TI-DI-AITM和NI-TI-DI-AITM为Inception v3、Inception v4、Inception ResNet v2和ResNet v2-101的模型集成生成的。

---

结论-Conclusion

该部分总结了AI - FGTM方法的优势及研究意义，具体如下：

1. 方法优势：提出AI - FGTM方法用于生成难以区分且迁移性强的对抗样本。该方法改进了基本符号结构的主要梯度处理步骤，克服了现有基于基本符号方法的局限。在与ImageNet兼容的数据集上进行大量实验，结果表明该方法在不增加运行时间和资源的情况下，能生成更难以区分的对抗样本，且攻击成功率更高。
2. 攻击效果：性能最佳的NI - TI - DI - AITM攻击方法，对六个经典防御模型的平均成功率达89.3%，对三个先进防御模型的平均成功率为82.7%，优于当前最先进的基于梯度的攻击方法。同时，该方法能将平均扰动降低近20%。
3. 研究意义：AI - FGTM为生成具有更好迁移性和不可区分性的对抗样本提供了新的基线。其良好的攻击效果对更有效防御模型的开发提出了安全挑战，推动了对抗样本防御技术的进一步研究 。