ICCV2023 | GRA | 通过梯度相关攻击提高对抗性迁移性

最新推荐文章于 2025-03-17 13:40:11 发布

四口鲸鱼爱吃盐

最新推荐文章于 2025-03-17 13:40:11 发布

阅读量1.4k

点赞数 34

分类专栏：文献阅读文章标签：深度学习人工智能对抗样本 dnn 神经网络

本文链接：https://blog.csdn.net/qq_60090693/article/details/145566711

版权

文献阅读专栏收录该内容

133 篇文章

订阅专栏

Boosting Adversarial Transferability via Gradient Relevance Attack

摘要-Abstract
引言-Introduction
相关工作-Related Work
方法-Approach
实验-Experiments
结论与讨论-Conclusion And Discussion

论文链接

本文 “Boosting Adversarial Transferability via Gradient Relevance Attack” 提出梯度相关攻击（GRA）方法，通过设计梯度相关框架挖掘输入邻域信息，利用衰减指标应对对抗扰动符号波动，提升了对抗样本的可迁移性，实验验证了该方法在多种模型上的有效性。

摘要-Abstract

Plentiful adversarial attack researches have revealed the fragility of deep neural networks (DNNs), where the imperceptible perturbations can cause drastic changes in the output. Among the diverse types of attack methods, gradient-based attacks are powerful and easy to implement, arousing wide concern for the security problem of DNNs. However, under the black-box setting, the existing gradient-based attacks have much trouble in breaking through DNN models with defense technologies, especially those adversarially trained models. To make adversarial examples more transferable, in this paper, we explore the fluctuation phenomenon on the plus-minus sign of the adversarial perturbations’ pixels during the generation of adversarial examples, and propose an ingenious Gradient Relevance Attack (GRA). Specifically, two gradient relevance frameworks are presented to better utilize the information in the neighborhood of the input, which can correct the update direction adaptively. Then we adjust the update step at each iteration with a decay indicator to counter the fluctuation. Experiment results on a subset of the ILSVRC 2012 validation set forcefully verify the effectiveness of GRA. Furthermore, the attack success rates of 68.7% and 64.8% on Tencent Cloud and Baidu AI Cloud further indicate that GRA can craft adversarial examples with the ability to transfer across both datasets and model architectures.

大量对抗攻击研究揭示了深度神经网络（DNN）的脆弱性，即难以察觉的扰动就能导致其输出发生剧烈变化。在众多攻击方法中，基于梯度的攻击方法强大且易于实施，这引发了人们对DNN安全问题的广泛关注。然而，在黑盒设置下，现有的基于梯度的攻击方法很难突破采用了防御技术的DNN模型，尤其是那些经过对抗训练的模型。为了使对抗样本更具可迁移性，本文探究了在生成对抗样本过程中，对抗扰动像素正负号的波动现象，并提出了一种巧妙的梯度相关性攻击（GRA）方法。具体而言，我们提出了两种梯度相关性框架，以更好地利用输入邻域的信息，从而自适应地修正更新方向。然后，我们使用一个衰减指标在每次迭代时调整更新步长，以应对这种波动。在ILSVRC 2012验证集的一个子集上的实验结果有力地验证了GRA的有效性。此外，在腾讯云和百度智能云上68.7%和64.8%的攻击成功率进一步表明，GRA生成的对抗样本能够跨数据集和模型架构迁移。

引言-Introduction

这部分主要介绍了研究的背景和动机，指出深度神经网络（DNNs）在取得成果的同时存在易受对抗样本攻击的问题，尤其是在黑盒攻击场景下现有基于梯度的攻击方法对有防御机制的模型效果不佳，进而提出了梯度相关性攻击（GRA）方法，具体内容如下：

研究背景：DNNs在多个领域成果丰硕，但在计算机视觉领域，其对人类难以察觉的恶意扰动极为敏感。生成具有强可迁移性的对抗样本，对揭示模型安全缺陷和探索内部机制意义重大，这成为计算机视觉领域的关键任务。
攻击设置及现有方法局限：攻击设置分为黑盒和白盒两种。白盒设置下攻击者可获取模型所有信息，许多攻击方法能实现近100%的攻击成功率；而黑盒设置下攻击者仅能获取模型输出，这使得攻击性能下降，尤其是面对有防御机制的模型。近年来提出多种方法应对这一问题，如基于梯度的攻击方法、输入增强变换和集成策略等，但现有方法存在不足，如方差调整（VT）未充分利用输入与邻域的梯度相关性。
提出GRA方法：受点积注意力框架启发，设计两个梯度相关性框架挖掘邻域信息，通过余弦相似度确定更新方向。研究发现对抗扰动符号的波动及固定步长影响对抗样本生成，因此引入衰减指标调整步长。将MI-FGSM与梯度相关性框架和衰减指标结合，提出GRA方法。实验证明GRA性能优于其他先进攻击方法，平均攻击成功率可达83.0%，比其他方法至少提高12.3%。

图1. 干净图像及其在Inception-v3上由梯度相关性攻击（GRA）生成的对抗样本的注意力图。目标模型是ResNet-152。

图2. 两种像素变化趋势的示意图：(a) 对抗样本的像素值变化；(b) 对抗扰动的符号变化。请注意，对抗样本是在Inception-v3模型上生成的。

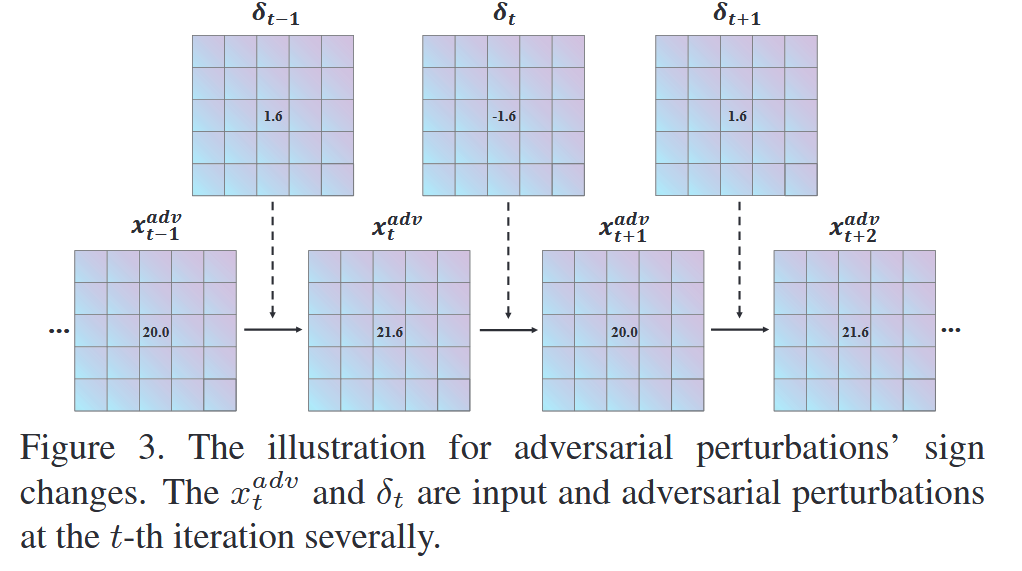
图3. 对抗扰动符号变化的示意图。 $x_{t}^{adv}$ 和 $\delta_{t}$ 分别是第 $t$ 次迭代时的输入和对抗扰动。
研究贡献：探索了对抗样本生成中对抗扰动符号的波动现象，并设计步长衰减指标应对；提出两种梯度相关性框架，充分利用输入邻域信息；结合当前输入增强变换提出GRA方法，显著提升对抗样本的可迁移性。综合实验表明GRA优于最新的基于梯度的攻击方法。

方法-Approach

本文该部分详细介绍了所提攻击方法的相关理论与机制，通过引入梯度相关性框架和衰减指标，改进现有攻击方法，提升对抗样本生成效果与攻击性能，具体内容如下：

初步知识：任务是寻找能欺骗目标分类器 $F_{\theta}$ 的对抗样本 $x^{adv}=x^{clean}+\delta$ ，需满足 $F_{\theta}(x^{clean})\neq F_{\theta}(x^{adv})$ 且 $\|\delta\|_{\infty}<\varepsilon$ 。在白盒设置下，可将其看作优化问题求解；但在黑盒设置中，通常用源模型 $F_{\psi}$ 生成对抗样本攻击目标模型，这种能成功欺骗其他模型的能力被称为对抗迁移性。
梯度相关性框架：方差调整（VT）利用上一次迭代的梯度方差修正当前梯度，但无法准确反映当前迭代损失函数的变化趋势。本文提出新方式，利用当前迭代的邻域信息修正当前梯度。通过采样得到附近图像 $x_{t}^{i}=x_{t}^{adv}+\gamma_{t}^{i}$ ，计算当前梯度 $G_{t}(x)$ 与 $x_{t}^{i}$ 上计算的梯度 $G_{t}^{i}(x)$ 的相关性。受点积注意力框架启发，提出两种框架：
- 个体梯度相关性框架：将 $G_{t}(x)$ 视为查询向量， $G_{t}^{i}(x)$ 视为键向量，通过余弦相似度 $s_{t}^{i}=\frac{G_{t}(x)\cdot G_{t}^{i}(x)}{\|G_{t}(x)\|_{2}\cdot\|G_{t}^{i}(x)\|_{2}}$ 建立相关性，得到加权梯度 $WG_{t}^{i}=s_{t}^{i}\cdot G_{t}+(1 - s_{t}^{i})\cdot G_{t}^{i}$ ，再计算全局加权梯度 $WG_{t}=\frac{1}{m}\sum_{i = 1}^{m}WG_{t}^{i}$ 。
- 平均梯度相关性框架：为提高效率，直接计算 $G_{t}(x)$ 与邻域平均梯度 $\overline{G_{t}}(x)=\frac{1}{m}\sum_{i = 1}^{m}G_{t}^{i}(x)$ 的相关性。通过余弦相似度 $s_{t}=\frac{G_{t}(x)\cdot\overline{G_{t}}(x)}{\|G_{t}(x)\|_{2}\cdot\|\overline{G_{t}}(x)\|_{2}}$ ，得到全局加权梯度 $WG_{t}=s_{t}\cdot G_{t}+(1 - s_{t})\cdot\overline{G_{t}}$ 。该框架中平均梯度可视为辅助修正项，根据当前梯度与平均梯度的相似程度分配权重。这两种框架都基于当前迭代邻域信息，与VT基于上一次迭代信息不同，且都可与MI - FGSM结合。
  
  图4. 两种梯度相关性框架示意图：(a) 个体梯度相关性框架；(b) 平均梯度相关性框架。
衰减指标：对抗扰动符号的波动和固定步长会使对抗样本在最优解附近振荡。由于对抗扰动符号取决于动量积累符号，定义衰减指标 $M_{t + 1}=M_{t}\odot(M_{t + 1}^{e}+\eta\cdot M_{t + 1}^{d})$ 。其中， $M_{t + 1}^{e}$ 和 $M_{t + 1}^{d}$ 分别表示相邻两次迭代中对抗扰动不变和变化的位置。若符号无波动，保持固定步长；若像素符号反复波动，表明该像素值可能接近最优解，通过衰减因子 $\eta$ 减小步长使其更接近最优解。每次迭代的更新过程为 $x_{t + 1}^{adv}=Clip\{x_{t}^{adv}+\alpha\cdot M_{t + 1}\odot sign(g_{t + 1})\}$ 。将MI - FGSM与平均梯度相关性框架和衰减指标结合，得到梯度相关性攻击（GRA）算法；与个体梯度相关性框架结合时记为I - GRA，用于区分两种框架。

图5. 对抗扰动符号出现波动时的两种情况：(a) 没有衰减指标；(b) 有衰减指标

实验-Experiments

这部分主要介绍了针对梯度相关性攻击（GRA）所开展的实验，通过多组实验验证了GRA的有效性，具体内容如下：

实验设置
- 数据集：沿用前人做法，选取ILSVRC 2012验证集中的1000张干净图像，这些图像能被本文所涉模型几乎100%准确分类。
- 模型：选择Inceptionv3、Inception-v4、Inception-Resnetv2和Resnet-v2-101作为源模型来生成对抗样本；目标模型包含上述源模型、对抗训练模型（如adv-Inceptionv3等），还考虑了与五种防御方法（PD、NRP、JPEG、ComDefend和FD ）结合的模型，另外对两个实际在线模型进行攻击测试。
- 参数设置：参考前人工作设置攻击参数，如迭代次数 $T$ 设为10，扰动幅度上限 $ε$ 设为16 ，步长 $α$ 设为1.6等，同时对不同攻击方法的特定参数进行设定。
单一方法攻击：用VTMI、VTNI、Admix、I-GRA和GRA在四个源模型上生成对抗样本，攻击七个目标模型。结果显示，GRA在多数正常训练模型和对抗训练模型上的攻击成功率高于其他方法；I-GRA和GRA大多情况下优于对比方法，且GRA略胜I-GRA，后续实验为简化仅采用GRA。

表1. 单次攻击对七个模型的攻击成功率（%）。对抗样本分别在Inception-v3、Inception-v4、Inception-Resnet-v2和ResNet-101上生成。 $*$ 表示白盒攻击的成功率，加粗结果为最优。
组合变换攻击：探究GRA与组合变换（CT，包含DI、TI和SI）的兼容性。实验表明，GRA-CT的攻击成功率最高，证实GRA与其他变换兼容性良好。

表2. 四种基于梯度的迭代攻击结合组合变换（CT）对七个模型的攻击成功率（%）。对抗样本分别在Inception-v3、Inception-v4、Inception-ResNet-v2和ResNet-101上生成。 $*$ 表示白盒攻击的成功率，加粗的结果是最优的。
集成策略攻击：运用集成策略增强GRA，攻击九个防御模型，并在两个在线模型上测试。结果显示，GRA在集成策略下平均攻击成功率达83.0%，对在线模型的攻击成功率分别为68.7%和64.8% ，均优于VTNI和Admix，凸显其有效性和对现实世界模型的威胁。

表3. 由在Inception-v3、Inception-v4、Inception-ResNet-v2和ResNet-101上同步生成的对抗样本对九个防御模型的攻击成功率（%）。加粗的结果为最佳。

表4. 采用集成策略生成的对抗样本对两个在线模型的攻击成功率（%）。加粗的结果是最佳的。
消融研究：分析GRA中样本数量 $m$ 、样本范围上界因子 $β$ 和衰减因子 $η$ 三个关键超参数的影响。 $m$ 增加时，正常训练模型上攻击成功率快速上升， $m = 20$ 后趋于稳定，对抗训练模型上 $m > 50$ 时仍有上升趋势； $β = 3.5$ 时，GRA在目标模型上成功率最高；衰减因子 $η$ 接近 $0.94$ 时，正常训练模型和对抗训练模型的平均攻击成功率都较高。

图6. 在Inception-v3上生成对抗样本时，梯度相关性攻击（GRA）在不同样本数量下的攻击成功率（%）。请注意，此处样本范围上界因子 $β = 3.5$ ，衰减因子 $η = 0.94$ 。

图7. 在Inception-v3上生成对抗样本时，梯度相关性攻击（GRA）在样本范围因子 $β$ 取不同上界时的攻击成功率（%）。请注意，此处样本数量 $m = 20$ ，衰减因子 $\eta = 0.94$ 。

图8. 在梯度相关性攻击（GRA）下，对抗样本在Inception-v3上生成时，两组模型（正常训练组和对抗训练组）在不同衰减因子 $η$ 下的平均攻击成功率（%）。请注意，此处样本数量 $m = 20$ ，样本范围上界因子 $β = 3.5$ .

结论与讨论-Conclusion And Discussion

这部分对研究进行了全面总结，并对未来基于梯度的攻击方法发展方向进行了探讨，具体内容如下：

研究结论：提出了梯度相关性攻击（GRA）方法，并对生成对抗样本过程中对抗扰动像素正负号的波动现象进行了探索。设计了两种梯度相关性框架来挖掘输入周围的潜在邻域信息，综合考虑余弦相似度计算效率和攻击性能，在GRA中采用平均梯度相关性框架。同时，设计了衰减指标，在遇到频繁波动时减小步长。在ILSVRC 2012验证集子集上进行的大量实验，有力地验证了GRA的优越性。此外，利用GRA生成的对抗样本对两个实际在线模型进行测试，揭示了现实世界中部署的模型可能存在不可靠的问题。
未来展望：认为未来基于梯度的攻击方法的改进可集中在两个方面。一方面是开发有效利用额外信息的方法，目前增强输入数据的方法众多，但充分利用这些信息的方法较少；另一方面是设计更合适的步长微调方式，使更新方向更加合理。