Transferability Bound Theory: Exploring Relationship between Adversarial Transferability and Flatness
本文 “Transferability Bound Theory: Exploring Relationship between Adversarial Transferability and Flatness” 提出对抗样本可迁移性的理论边界,证明平坦性与可迁移性无必然联系,并基于理论分析提出 TPA 攻击方法,通过实验验证其在多种场景下的有效性。
摘要-Abstract
A prevailing belief in attack and defense community is that the higher flatness of adversarial examples enables their better cross-model transferability, leading to a growing interest in employing sharpness-aware minimization and its variants. However, the theoretical relationship between the transferability of adversarial examples and their flatness has not been well established, making the belief questionable. To bridge this gap, we embark on a theoretical investigation and, for the first time, derive a theoretical bound for the transferability of adversarial examples with few practical assumptions. Our analysis challenges this belief by demonstrating that the increased flatness of adversarial examples does not necessarily guarantee improved transferability. Moreover, building upon the theoretical analysis, we propose TPA, a Theoretically Provable Attack that optimizes a surrogate of the derived bound to craft adversarial examples. Extensive experiments across widely used benchmark datasets and various real-world applications show that TPA can craft more transferable adversarial examples compared to state-of-the-art baselines. We hope that these results can recalibrate preconceived impressions within the community and facilitate the development of stronger adversarial attack and defense mechanisms.
在攻防领域,一种普遍的观点认为,对抗样本的平坦度越高,其跨模型可迁移性就越好,这使得人们对使用锐度感知最小化及其变体的兴趣日益浓厚。然而,对抗样本的可迁移性与其平坦度之间的理论关系尚未得到很好的确立,这使得这种观点值得怀疑。为了填补这一空白,我们进行了理论研究,并首次在极少实际假设的情况下,推导出了对抗样本可迁移性的理论边界。我们的分析表明,对抗样本平坦度的增加并不一定能保证可迁移性的提高,这对上述观点提出了挑战。此外,基于理论分析,我们提出了TPA(理论可证攻击)方法,它通过优化所推导边界的替代指标来生成对抗样本。在广泛使用的基准数据集和各种实际应用中进行的大量实验表明,与最先进的基线方法相比,TPA能够生成更具可迁移性的对抗样本。我们希望这些结果能够重新校准该领域内的先入之见,并推动更强有力的对抗攻击和防御机制的发展。
引言-Introduction
该部分内容主要阐述研究背景和研究问题,指出当前对抗样本可迁移性研究中存在的问题,引出本文的研究重点,具体内容如下:
- 研究背景:对抗样本可迁移性指其能误导不同参数和架构的目标模型,在模型鲁棒性评估和数据隐私保护等方面意义重大。但现有生成的对抗样本常对代理模型过度适配,可迁移性受限,因此研究者致力于开发增强可迁移性的技术。其中,受模型泛化能力与损失曲面平坦性关联的启发,基于平坦性的方法成为热点,如 Admix 借鉴Mixup思想,Foret等人提出优化小扰动半径内的最坏情况损失来调节损失曲面,此类方法的实证效果显著,引发了对其变体的研究热潮。
- 研究问题:尽管基于平坦性的增强可迁移性技术在实证上表现出色,但对抗样本可迁移性与平坦性的理论关系并未明确。目前尚不清楚收敛到平坦极值点的对抗样本是否必然具有更好的可迁移性,因为平坦性与泛化能力的关系仍有争议,这使得可迁移性与平坦性的关系更加扑朔迷离。基于此,本文旨在理论上探究两个关键问题:一是平坦对抗样本是否必然与可迁移性提升相关;二是理论分析能否指导开发更具原则性的基于迁移的攻击方法。针对第二个问题,本文提出理论可证攻击(TPA),通过优化推导边界的替代指标来生成对抗样本,且该方法在基准测试和实际应用中表现优异。
相关工作-Related Work
该部分主要介绍了与本文研究相关的两类工作,分别是基于平坦性的优化方法和增强可迁移性的方法,具体内容如下:
- 基于平坦性的优化方法:直观上,模型在训练数据上的损失曲面可近似测试数据上的情况,因此平坦极值点被认为比尖锐极值点在训练和测试数据间的性能差距更小,即具有更好的泛化能力。基于此,SAM等方法将平坦性项或其变体融入损失函数以提升模型泛化能力,如通过公式 max ∥ ρ ∥ ≤ ϵ L ( F θ + ρ ( x ) , y ) − L ( F θ ( x ) , y ) \max_{\|\rho\| \leq \epsilon} \mathcal{L}(F_{\theta+\rho}(x), y)-\mathcal{L}(F_{\theta}(x), y) max∥ρ∥≤ϵL(Fθ+ρ(x),y)−L(Fθ(x),y) 量化从 θ \theta θ 移动到相邻最差参数值时损失的增加量,以此评估损失曲面在 θ \theta θ 点的平坦度 。后续研究探索了多种平坦性度量指标,如Fisher行列式和梯度范数等用于正则化损失曲面。然而,近期研究对此提出质疑,Dinh等人证明存在损失曲面尖锐但在测试数据上表现良好的网络;Andriushchenko等人通过实验揭示在大型神经网络中,平坦性与泛化能力并无强相关性。
- 增强可迁移性的方法:这类方法大致可分为基于输入正则化、基于优化和基于模型的方法。
- 基于输入正则化的方法:在每次迭代中,通过集成多个变换后的输入来生成对抗样本,不同方法的区别在于所采用的变换技术。例如,DI 提出对输入进行缩放和填充,TI 对输入进行平移,SI 对输入进行缩放;Admix 尝试将输入与其他类别的图像混合;SSA 在频域中对输入进行扰动以产生更多样化的变换输入;BSR 将输入分割为不重叠的块,随机打乱和旋转这些块。
- 基于优化的方法:利用更先进的优化器,如 MI 采用Momentum优化器,以增强对抗样本的可迁移性。
- 基于模型的方法:从模型本身的角度增强可迁移性,例如 SGM 改进反向传播过程以放大早期层的梯度,因为早期层学习的特征在不同模型中更具共享性;StyLess使用风格化网络防止对抗样本使用非鲁棒的风格特征。此外,一些研究探索基于平坦性的优化方法来提高对抗样本的可迁移性,如Qin等人引入 RAP,通过调整公式(如上述SAM中的公式)来生成平坦度增强的对抗样本;还有研究选择惩罚生成的对抗样本的梯度。
理论分析-Theoretical Analysis
该部分主要对对抗样本的可迁移性展开理论探索,通过设定假设、推导定理,深入分析了影响对抗样本可迁移性的因素,具体内容如下:
- 理论分析的基础设定:从基于迁移的对抗攻击的标准设置出发,其主要目标是让基于本地代理模型 F F F 生成的对抗样本对目标模型 F ′ F' F′ 尽可能有效。对于给定的自然样本 x x x 及其真实标签 y y y,普通的基于迁移的攻击通过求解优化任务来为 x x x 生成对抗噪声 δ ∗ \delta^{*} δ∗,即 δ ∗ = a r g m i n δ − L ( F ( x + δ ) , y ) , s . t . , ∥ δ ∥ ∞ ≤ ϵ \delta^{*}=\underset{\delta}{arg min }-\mathcal{L}(F(x+\delta), y), s.t., \| \delta\| _{\infty} \leq \epsilon δ∗=δargmin−L(F(x+δ),y),s.t.,∥δ∥∞≤ϵ,其中 L \mathcal{L} L 为交叉熵损失, ϵ \epsilon ϵ 为扰动预算。为更好地研究对抗样本的可迁移性问题,将其分解为两个因素:局部有效性项,用于衡量生成的对抗样本在代理模型上的损失;迁移相关损失项,用于量化对抗样本从代理模型迁移到目标模型时损失的变化,分别用 L ( F ( x + δ ) , y ) L(F(x+\delta), y) L(F(x+δ),y) 和 D ( x + δ , y ) = L ( F ′ ( x + δ ) , y ) − L ( F ( x + δ ) , y ) D(x+\delta, y)=L(F'(x+\delta), y)-L(F(x+\delta), y) D(x+δ,y)=L(F′(x+δ),y)−L(F(x+δ),y) 来评估。
- 理论假设
- 假设3.1: x x x 的潜在分布是连续且有界的,存在常数 B 1 B_{1} B1,使得对于任意 x x x,有 p ( x ) ≤ B 1 p(x) ≤B_{1} p(x)≤B1。
- 假设3.2: p ( x ) p(x) p(x) 的梯度范数是有界的,存在常数 B 2 B_{2} B2,使得对于任意 x x x,有 ∥ ∇ p ( x ) ∥ ≤ B 2 \|\nabla p(x)\| ≤B_{2} ∥∇p(x)∥≤B2。
- 假设3.3:对抗样本在自然中出现的概率小于自然样本,即 p ( x + δ ) ≤ p ( x ) p(x+\delta) ≤p(x) p(x+δ)≤p(x)。
- 假设3.4:代理模型生成的对抗样本在代理模型上的损失大于在目标模型上的损失,即 L ( F ′ ( x + δ ) , y ) ≤ L ( F ( x + δ ) , y ) L(F'(x+\delta), y) ≤L(F(x+\delta), y) L(F′(x+δ),y)≤L(F(x+δ),y)。
- 假设3.5:代理模型基于类似ResNet的架构,每一层应用线性变换后接ReLU激活函数。
- 定理推导与分析
- 定理3.1:(具体证明见原文的附录)在假设3.1 - 3.5成立的情况下,对于较小的 ∥ δ ∥ 2 2 \|\delta\|_{2}^{2} ∥δ∥22,有 E p ( x ) { ∥ D ( x + δ , y ) ∥ 2 2 } ≤ E p ( x ) { ∥ D ( x , y ) ∥ 2 2 + C ∥ δ ∥ 2 2 ∥ ∇ D ( x , y ) ∥ 2 2 } ⏟ T h e i n h e r e n t m o d e l d i f f e r e n c e c o m p o n e n t + ( 1 + C ) E p ( x ) { ∥ δ ∥ 2 2 ∥ ∇ l o g F ( x + δ ) ∥ 2 2 } ⏟ T h e f i r s t − o r d e r g r a d i e n t c o m p o n e n t + 2 E p ( x ) { ∥ δ ∥ 2 2 ∑ i ∣ ∇ 2 l o g F ( x + δ ) [ i , i ] ∣ } ⏟ T h e s e c o n d − o r d e r g r a d i e n t c o m p o n e n t \mathbb{E}_{p(x)}\left\{\| D(x+\delta, y)\| _{2}^{2}\right\} \leq \underbrace{\mathbb{E}_{p(x)}\left\{\| D(x, y)\| _{2}^{2}+C\| \delta\| _{2}^{2}\| \nabla D(x, y)\| _{2}^{2}\right\}}_{The\ \ inherent\ \ model\ \ difference\ \ component }+\underbrace{(1+C) \mathbb{E}_{p(x)}\left\{\| \delta\| _{2}^{2}\| \nabla log F(x+\delta)\| _{2}^{2}\right\}}_{The\ \ first-order\ \ gradient\ \ component }+\underbrace{2 \mathbb{E}_{p(x)}\left\{\| \delta\| _{2}^{2} \sum_{i}\left|\nabla^{2} log F(x+\delta)[i, i]\right|\right\}}_{The\ \ second-order\ \ gradient\ \ component } Ep(x){∥D(x+δ,y)∥22}≤The inherent model difference component Ep(x){∥D(x,y)∥22+C∥δ∥22∥∇D(x,y)∥22}+The first−order gradient component (1+C)Ep(x){∥δ∥22∥∇logF(x+δ)∥22}+The second−order gradient component 2Ep(x){∥δ∥22i∑ ∇2logF(x+δ)[i,i] } ,其中 C = B 1 B 1 + B 2 ∥ δ ∥ 2 C=\frac{B_{1}}{B_{1}+B_{2}\|\delta\|}^{2} C=B1+B2∥δ∥B12, [ i , i ] [i, i] [i,i] 表示给定矩阵中第 i i i 行和第 j j j 列的元素。同时有 ∥ L ( F ′ ( x + δ ) , y ) ∥ 2 2 ≥ ∣ ( ∥ L ( F ( x + δ ) , y ) ∥ 2 2 − K ) ∣ \left\| \mathcal{L}\left(F'(x+\delta), y\right)\right\| _{2}^{2} \geq\left|\left(\| \mathcal{L}(F(x+\delta), y)\| _{2}^{2}-K\right)\right| ∥L(F′(x+δ),y)∥22≥ (∥L(F(x+δ),y)∥22−K) ,这里 K K K 为上述不等式右边三项之和。
- 对定理中各项的分析:
- 固有模型差异分量(The inherent model difference component,不等式右侧第一项):该分量通过评估代理模型和目标模型对自然样本 x x x 的输出差异,直观地衡量了两个模型的相似性。其值越高,代理模型生成的对抗样本就越难迁移到目标模型。在实际中,由于目标模型期望在 x x x 上表现良好、攻击者可微调代理模型使 x x x 在其中的损失较小,以及两个模型差异小时梯度差异也较小等原因,该分量的值往往不大。此外,该分量为合适代理模型的选择提供了标准,即代理模型对 x x x 的预测需与目标模型接近,放宽了对架构和数据相似性的要求。
- 一阶梯度分量和二阶梯度分量:定理中与
δ
\delta
δ 方向相关的因素包括一阶梯度和二阶梯度分量,一阶梯度分量可直接衡量对抗样本的平坦度。但二阶梯度分量的存在表明,可迁移性并非仅取决于平坦度。以函数
f
(
x
)
=
sin
(
x
2
)
f(x)=\sin(x^{2})
f(x)=sin(x2) 为例,优化其一阶梯度范数并不能得到优化其一阶梯度和二阶梯度范数之和的最优解,这凸显了仅最小化一阶梯度分量不足以确保最小化边界。

图1: y = sin x 2 y = \sin x^{2} y=sinx2 的一阶导数和二阶导数的可视化。黑色星号表示 y 1 y_1 y1 和 y 3 y_3 y3 取得最小值的位置。
提出的方法TPA-The Proposed Approach TPA
该部分详细介绍了基于理论分析提出的TPA(Theoretically Provable Attack)方法,涵盖方法概述、优化公式和近似求解三方面内容,具体如下:
- 方法概述:在上部分理论分析中,将对抗样本可迁移性分解为局部有效性项和迁移相关损失项,并推导了后者的边界。自然的想法是联合优化这两项,以生成更具可迁移性的对抗样本。其中,局部有效性项可维持生成的对抗样本对代理模型的攻击有效性,而迁移相关损失项的边界能控制对抗样本迁移到目标模型时的性能下降,从而实现更好的可迁移性。然而,原边界包含二阶梯度分量,优化成本高。因此,TPA提出用一个计算可行且理论上有效的替代项来代替原边界,通过理论验证确保其攻击有效性,并在下面介绍了对该优化目标的近似求解方法。
- 优化公式:TPA的优化目标形式化为
δ
∗
=
a
r
g
m
i
n
δ
−
L
(
F
(
x
+
δ
)
,
y
)
+
λ
E
Δ
∼
U
(
−
b
,
b
)
{
∥
∇
L
(
F
(
x
+
δ
+
Δ
)
,
y
)
∥
2
}
\delta^{*}=\underset{\delta}{arg min }-\mathcal{L}(F(x+\delta), y)+\lambda \mathbb{E}_{\Delta \sim U(-b, b)}\left\{\| \nabla \mathcal{L}(F(x+\delta+\Delta), y)\| _{2}\right\}
δ∗=δargmin−L(F(x+δ),y)+λEΔ∼U(−b,b){∥∇L(F(x+δ+Δ),y)∥2},约束条件为
∥
δ
∥
∞
≤
ϵ
,
b
≥
0
\| \delta\| _{\infty} \leq \epsilon, b \geq 0
∥δ∥∞≤ϵ,b≥0.
在这个公式中, − L ( F ( x + δ ) , y ) -L(F(x+\delta), y) −L(F(x+δ),y) 作为局部有效性项, ∥ ∇ L ( F ( x + δ + Δ ) , y ) ∥ 2 \| \nabla L(F(x+\delta+\Delta), y) \|_{2} ∥∇L(F(x+δ+Δ),y)∥2 充当推导边界的替代项。
该替代项旨在调节一阶梯度和二阶梯度分量,由于在特定扰动范数约束和代理 - 目标模型对下,固有模型差异分量为常数项,所以未包含在替代项中。
通过最小化样本 x + δ x+\delta x+δ 周围的梯度,直观上可使 x + δ x+\delta x+δ 本身的梯度范数减小。
理论上,二阶梯度用于量化一阶梯度的变化率,通过惩罚 x + δ x+\delta x+δ 周围样本的梯度范数,可使这些样本的梯度范数趋于零,进而隐式调节二阶梯度。具体证明为 ∑ i ∣ ∇ 2 l o g F ( x + δ ) [ i , i ] ∣ = ∑ i ∣ lim μ → 0 ∇ l o g F ( x + δ + μ ) [ i ] − ∇ l o g F ( x + δ ) [ i ] μ ∣ = ∥ lim μ → 0 { ( ∇ L ( F ( x + δ + μ ) , y ) − ∇ L ( F ( x + δ ) , y ) ) ⋅ 1 μ } ∥ 1 \sum_{i}\left|\nabla^{2} log F(x+\delta)[i, i]\right|=\sum_{i}\left|\lim _{\mu \to 0} \frac{\nabla log F(x+\delta+\mu)[i]-\nabla log F(x+\delta)[i]}{\mu}\right|=\| \lim _{\mu \to 0}\left\{(\nabla L(F(x+\delta+\mu), y)-\nabla L(F(x+\delta), y)) \cdot \frac{1}{\mu}\right\} \| _{1} ∑i ∇2logF(x+δ)[i,i] =∑i limμ→0μ∇logF(x+δ+μ)[i]−∇logF(x+δ)[i] =∥limμ→0{(∇L(F(x+δ+μ),y)−∇L(F(x+δ),y))⋅μ1}∥1,即当 x + δ x+\delta x+δ 周围样本的梯度范数趋于零时,二阶梯度分量也趋于零,说明该替代项能有效调节一阶梯度和二阶梯度。 - 近似求解:由于
F
(
⋅
)
F(\cdot)
F(⋅) 具有高度非线性和非凸性,难以直接求解公式中的解析解。标准做法是采用基于梯度的优化方法,但公式的梯度涉及在多个点
x
+
δ
+
Δ
i
x+\delta+\Delta_{i}
x+δ+Δi 处计算Hessian矩阵,在高维空间中计算成本极高。
为避免直接计算Hessian矩阵,利用泰勒展开对 H x + δ + Δ i ∇ L ( F ( x + δ + Δ i ) , y ) ∥ ∇ L ( F ( x + δ + Δ i ) , y ) ∥ 2 H_{x+\delta+\Delta_{i}} \frac{\nabla L(F(x+\delta+\Delta_{i}), y)}{\| \nabla L(F(x+\delta+\Delta_{i}), y) \|_{2}} Hx+δ+Δi∥∇L(F(x+δ+Δi),y)∥2∇L(F(x+δ+Δi),y) 进行近似估计。
假设 ϕ \phi ϕ 足够小,对 L ( F ( x + δ + Δ i + ϕ ) , y ) \mathcal{L}\left(F\left(x+\delta+\Delta_{i}+\phi\right), y\right) L(F(x+δ+Δi+ϕ),y) 进行泰勒展开得到 L ( F ( x + δ + Δ i + ϕ ) , y ) = L ( F ( x + δ + Δ i ) , y ) + ∇ L ( F ( x + δ + Δ i ) , y ) ϕ \mathcal{L}\left(F\left(x+\delta+\Delta_{i}+\phi\right), y\right)=\mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right)+\nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right) \phi L(F(x+δ+Δi+ϕ),y)=L(F(x+δ+Δi),y)+∇L(F(x+δ+Δi),y)ϕ,对其两边求导可得 ∇ L ( F ( x + δ + Δ i + ϕ ) , y ) = ∇ L ( F ( x + δ + Δ i ) , y ) + H x + δ + Δ i ϕ \nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}+\phi\right), y\right)=\nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right)+H_{x+\delta+\Delta_{i}} \phi ∇L(F(x+δ+Δi+ϕ),y)=∇L(F(x+δ+Δi),y)+Hx+δ+Δiϕ。
令 ϕ = k ∇ L ( F ( x + δ + Δ i ) , y ) ∥ ∇ L ( F ( x + δ + Δ i ) , y ) ∥ 2 \phi = k \frac{\nabla L(F(x+\delta+\Delta_{i}), y)}{\left\|\nabla L(F(x+\delta+\Delta_{i}), y)\right\|_{2}} ϕ=k∥∇L(F(x+δ+Δi),y)∥2∇L(F(x+δ+Δi),y)( k k k 为小常数),则 H x + δ + Δ i ∇ L ( F ( x + δ + Δ i ) , y ) ∥ ∇ L ( F ( x + δ + Δ i ) , y ) ∥ 2 = ∇ L ( F ( x + δ + Δ i + k ∇ L ( F ( x + δ + Δ i ) , y ) ∥ ∇ L ( F ( x + δ + Δ i ) , y ) ∥ 2 ) , y ) k − ∇ L ( F ( x + δ + Δ i ) , y ) k H_{x+\delta+\Delta_{i}} \frac{\nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right)}{\left\| \nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right)\right\| _{2}}=\frac{\nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}+k \frac{\nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right)}{\left\| \nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right)\right\| _{2}}\right), y\right)}{k}-\frac{\nabla \mathcal{L}\left(F\left(x+\delta+\Delta_{i}\right), y\right)}{k} Hx+δ+Δi∥∇L(F(x+δ+Δi),y)∥2∇L(F(x+δ+Δi),y)=k∇L(F(x+δ+Δi+k∥∇L(F(x+δ+Δi),y)∥2∇L(F(x+δ+Δi),y)),y)−k∇L(F(x+δ+Δi),y).
将该近似结果代入原梯度公式,得到公式的近似估计梯度。与直接计算Hessian矩阵相比,该近似求解仅涉及一阶梯度,计算时间为线性,提高了TPA的计算效率。同时,泰勒展开产生的近似误差为 O ( k ) O(k) O(k).
模拟实验-Simulation Experiment
该部分主要通过模拟实验对TPA方法进行评估,包括实验设置、攻击结果及分析,具体内容如下:
- 实验设置
- 数据集:从ImageNet中随机选取10000张图像。
- 模型:考虑14种模型,包括12种卷积神经网络(如ResNet50、DenseNet121等)和2种基于Transformer的架构(ViT和Swin),还在采用不同防御机制(如对抗训练、鲁棒训练)的安全模型上验证TPA性能。
- 基线方法:选取9种当前先进的攻击方法(如BIM、DI等)与TPA进行对比,其中Self-Universality是有针对性的攻击,仅报告其在有针对性设置下的性能。
- 评估指标:使用攻击成功率(ASR)作为评估指标,即对抗样本被目标模型误分类的比率。
- 超参数配置:基线方法采用其原始论文中的超参数设置,TPA的超参数设置为 λ = 5 \lambda = 5 λ=5, b = 16 b = 16 b=16, k = 0.05 k = 0.05 k=0.05, N = 10 N = 10 N=10,所有方法的迭代次数设为20, ϵ \epsilon ϵ 设为16,步长设为1.6。
- 攻击结果
-
对正常模型的攻击结果:在卷积神经网络和Transformer类神经网络上测试TPA的攻击效果。结果表明,TPA显著优于所有基线方法。以ResNet50为代理模型时,TPA的攻击成功率平均比当前最先进的基于迁移的攻击方法SSA高出约9%。
表1:不同攻击方法对正常模型的攻击成功率(%)。最佳结果以粗体显示。

-
对安全模型的攻击结果:在使用鲁棒训练防御的模型上评估TPA的有效性,实验采用未防御模型作为代理模型,这种设置下代理模型和目标模型差异更大,更具挑战性。结果显示,TPA仍能生成更具可迁移性的对抗样本,相较于SSA,其攻击成功率有大幅提升。
表2:不同方法在安全模型上的攻击成功率(%)。考虑了三种不同的鲁棒训练方法:使用 L 2 L_{2} L2 扰动的对抗训练( L 2 − { 0.03 − 5 } L2 - \{0.03-5\} L2−{0.03−5})、使用 L ∞ L_{\infty} L∞ 扰动的对抗训练(AdvIncV3和EnsAdvIncResV2)、使用风格化ImageNet(SIN)的鲁棒训练以及风格化和自然ImageNet混合(SIN - IN)的鲁棒训练。最佳结果以粗体显示。

-
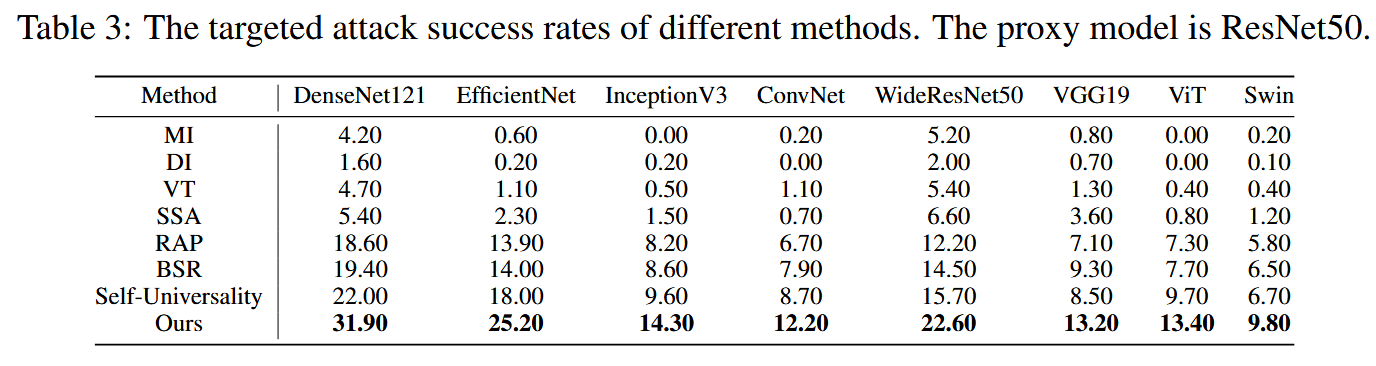
目标性攻击结果:研究TPA在目标性攻击场景下的有效性。结果表明,TPA在目标性攻击设置下的表现突出,即使与专门为目标性攻击设计的Self-Universality相比,也具有明显优势。
表3:不同方法的有针对性攻击成功率。代理模型为ResNet50。
-
不同扰动预算下的攻击结果:小扰动预算会增加基于迁移攻击的难度,通过改变扰动预算评估不同方法的攻击效果。实验结果显示,在不同扰动预算下,TPA的攻击成功率在所有设置中均处于领先地位。

图2:不同扰动预算下TPA的攻击效果。对抗样本由ResNet50生成。
-
现实世界应用中的评估-Evaluation in Real World Applications
该部分主要在实际应用场景中对TPA进行评估,展示了TPA在现实复杂环境下的有效性,具体内容如下:
- 评估原因:在实际应用中评估TPA性能更具挑战性,但也能带来更可靠的评估结果。这是因为现实应用具有独特的特点,包括使用复杂模型且可能包含实际防御机制、训练设置复杂多样、输出结构为多层级标签及置信度,与代理模型的输出空间差异大等。
- Google MLaaS平台:攻击Google Cloud Vision应用(包括图像分类和目标检测),这是一种先进的AI服务。通过为该应用生成100个对抗样本,收集其响应并让志愿者对样本与响应的一致性进行评分(1分表示完全错误,5分表示精确)来评估TPA。若得分1或2则视为攻击成功,实验结果显示图像分类和目标检测的攻击成功率分别约为70%和80%。同时发现无效对抗样本常涉及ImageNet中未涵盖的“Person”标签相关实体,这表明TPA未被引导去破坏“Person”的特征。
- 反向图像搜索引擎:测试TPA对Google、Bing、Yandex和Baidu这四款主流反向图像搜索引擎的攻击效果。复用为Google服务生成的对抗样本,根据检索图像与原始图像的相似度进行1 - 5分评分,分数与相似度成反比。结果表明,四款搜索引擎对TPA生成的对抗样本均存在显著漏洞,尤其是百度图片搜索,会返回完全不相关的图像。
- 多模态AI平台:在OpenAI和Amazon的多模态AI平台(GPT - 4和Claude3)上评估TPA。以得分1或2视为攻击成功,TPA在GPT - 4和Claude3上的攻击成功率分别高达56%和62%。例如,在一个示例中,GPT - 4和Claude3都未能准确识别图像内容,将绿色水果误判为其他物体。
表4:对抗样本对现实世界应用有效性的评分。我们从ImageNet中随机抽取100个样本,使用TPA和ResNet50为它们生成对抗样本。我们招募了一名志愿者来评估图像内容与应用程序所做预测之间的一致性。评分越低,攻击的有效性越高。


图3:例子.
GPT-4的回应:这张图片看起来像是一幅数字绘画,或者是在一张用刀切绿色卷心菜或生菜的照片上添加了类似动画故障的效果。图片色彩鲜艳,从动作上看,刀正在切蔬菜。
Claude3回应:这张图片展示了各种装满不同种类农产品和蔬菜的塑料袋。袋子里装着生菜或绿叶蔬菜、胡萝卜,还有看起来像是某种香草或绿色植物。塑料袋能让人从外面看到里面的东西。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










