Codeforces Round 906 (Div. 2)个人题解（A-D)

目录

A. Doremy's Paint 3

B. Qingshan Loves Strings

C. Qingshan Loves Strings 2

D. Doremy's Connecting Plan

---

A. Doremy's Paint 3

由a1+a2==a2+a3可得

a1==a3

同理：a3==a5,a5==a6

可知奇数位相等，同理偶数位也相等。

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long 
const int N=1e6+10;
int n;
void solve()
{
	cin>>n;
	unordered_map<int,int>r;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		r[x]++;
	}
	if(r.size()>=3)cout<<"No"<<endl;
	else if(r.size()==1)cout<<"Yes"<<endl;
	else 
	{
		vector<int>aas;
		for(auto i:r)aas.push_back(i.second);
		if(n%2==0)
		{
			if(aas[0]==aas[1])cout<<"Yes"<<endl;
			else cout<<"No"<<endl;
		}
		else 
		{
			if(abs(aas[0]-aas[1])==1)cout<<"Yes"<<endl;
			else cout<<"No"<<endl;
		}
	}
}
signed main()
{
	int T=1;
	cin>>T;
	while(T--)solve();
	return 0;
} 

B. Qingshan Loves Strings

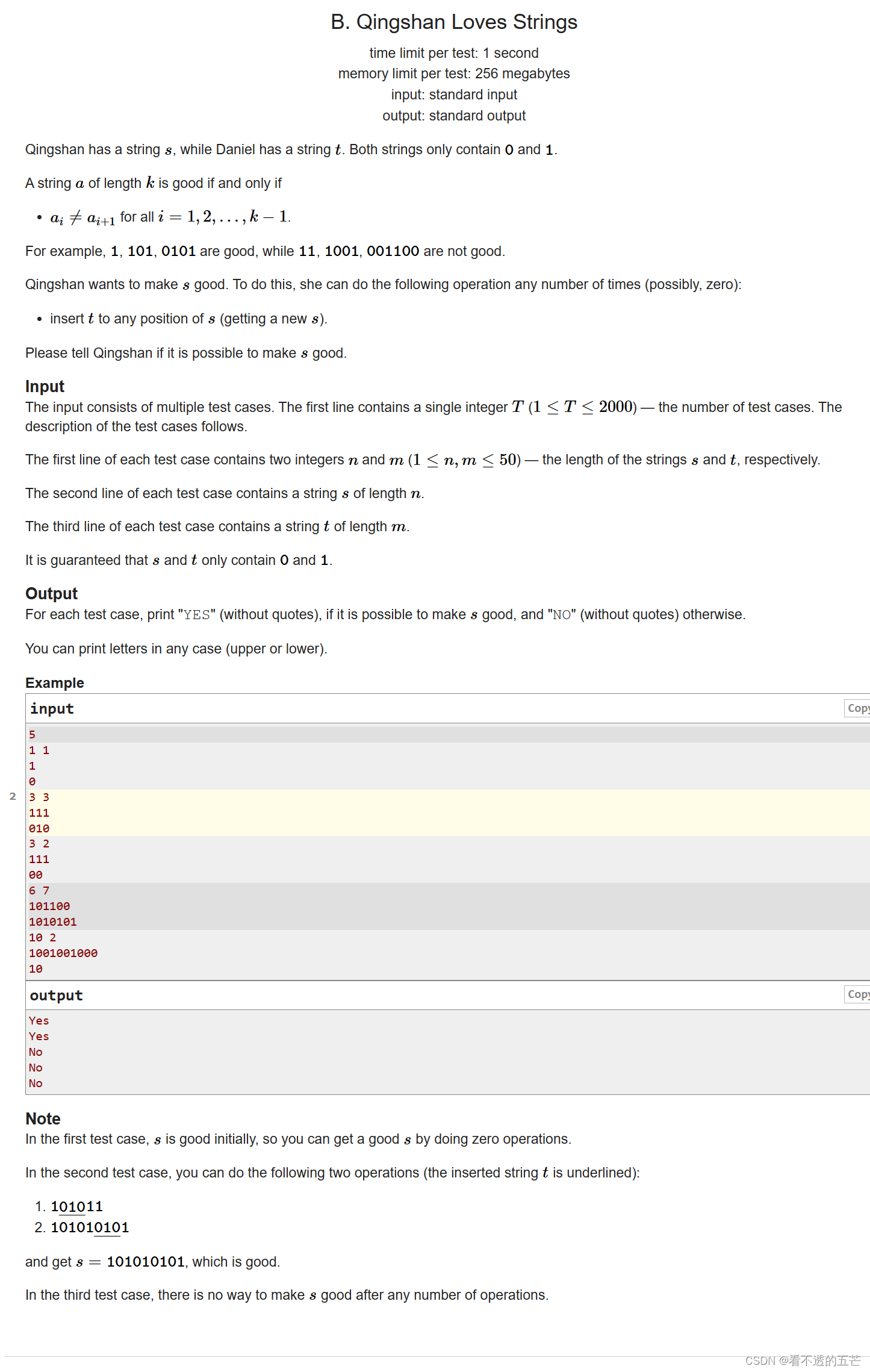
可以将s中出现重复位置的地方插入t字符串，然后进行暴力判断。也可以分类讨论，但是写起来相对复杂，建议用前者的方法。

分类讨论代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long 
const int N=1e6+10;
int n,m;
void solve()
{
	cin>>n>>m;
	string s,t;
	cin>>s>>t;
	char sh='9';
	int flag=0;
	char fg;
	int sum=0;
	set<char>aas;
	for(int i=0;i<s.size()-1;i++)
	{
		if(s[i]==s[i+1])
		{
			aas.insert(s[i]);
			fg=s[i];
		}
	}
	sum=aas.size();
	for(int i=0;i<t.size();i++)
	{
		if(sh==t[i])
		{
			flag=1;
			break;
		}
		sh=t[i];
	}
	if(flag==1)
	{
		if(sum)cout<<"NO"<<endl;
		else cout<<"YES"<<endl;
	}
	else 
	{
		if(sum==2)cout<<"NO"<<endl;
		else if(sum==1)
		{
			char p=t[0];
			if(t[0]-t[(int)t.size()-1])
			{
				cout<<"NO"<<endl;
			}
			else 
			{
				if(p-fg)cout<<"YES"<<endl;
				else cout<<"NO"<<endl;
			}
		}
		else cout<<"YES"<<endl;
	}
}
signed main()
{
	int T=1;
	cin>>T;
	while(T--)solve();
	return 0;
} 

C. Qingshan Loves Strings 2

题目条件分析：

给出对象：给出一个字符串，

操作方式：要求从中添加“01”串，

目标对象：使得中心对称的位置不相等。

目标特性：0和1的数量相等，并且字符数量是偶数。

操作方式特性：添加的“01”当中0和1的数量相等。并且可以在任意位置进行插入。

思路：

首先判断字符串s长度是否为偶数并且0和1的数量是否相等。

如果不满足输出-1，满足的情况一定有解。

构造策略：从左右两端开始构造，如果左右两端字符不同，那么两端指针向中间前进。如果相等，那么分情况讨论。

1、两端都为0，即0.....0。显然可以将其变成0.....01。这样左右两端不相同了。

2、两端都为1，即1.....1。显然可以将其变成011...1。这样左右两端不相同了。

将其变为不同后左右指针向中间前进，重复该操作。最终一定可以得到满足需求的字符串。

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define PII pair<int,int>
#define endl "\n"
const int N=1e6+10;
void solve()
{
	int n;
	cin>>n;
	string s;
	cin>>s;
	int flag=0,sum=0,ssm=0;
	for(int i=0;i<s.size();i++)
	{
		if(s[i]=='0')sum++;
	}
	vector<int>ans;
	if(n%2==1||n/2-sum)cout<<"-1"<<endl;
	else 
	{
//		int l=0,r=(int)s.size()-1;
		while(ssm*2<(int)s.size())
		{
			if(s[ssm]-s[(int)s.size()-1-ssm])ssm++;
			else 
			{
				if(s[ssm]=='0')
				{
					ans.push_back((int)s.size()-ssm);
					s.insert((int)s.size()-ssm,"01");
				}
				else
				{
					ans.push_back(0+ssm);
					s.insert(ssm,"01");
				}
			}
		}
		cout<<ans.size()<<endl;
		for(int i=0;i<ans.size();i++)cout<<ans[i]<<" ";
		cout<<endl;
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	int T=1;
	cin>>T;
	while(T--)solve();
	return 0;
} 

D. Doremy's Connecting Plan

题目条件分析：

给出对象：给出n个点的权值。

操作方式：每个点有个权值wi,编号为i。如果两个点所在联通分量权值之和大于两个点乘积再乘常数c。那么两个点可以相连。

目标对象：一个完整的强连通图。

目标特性：任意两点之间存在路径可达。

操作方式特性：两点的连接和两联通分量和有关，和越大，并且下标乘积越小，可连性越强。

思路：

1、首先我们的目标是构成一个强连通图。所有我们可以对单个强连通分量进行分析，想要将两个强连通分量相连，首先必须找出两个强连通分量各自编号的最小值进行相连，因为无论选择哪两个点，其和都是固定的。但是编号乘积不同。

2、根据（1）所介绍的性质，我们可以认为，两个点相连等价于相容为一个新的点，新的点的编号为两点编号的最小值，新点的权值为两点权值的和。

3、猜测以1为目标与其它相连接一定是存在可连的，如果1和其它点都不可连，那么其余任何两个点都不可连。证明猜测的方式很简单：假设编号为1的点和a点不可连，编号为1的点与b点也不可怜，假设a点和b点可连，得到矛盾的结论。因此假设成立。具体证明过程可自行实现，不难证明。

综上所述

代码如下:

#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define PII pair<int,int>
#define endl "\n"
const int N=1e6+10;
int arr[N];
int n,c;
struct nood{
	int w,id;
};
bool cmp(nood A,nood B)
{
	return A.w-A.id*c>B.w-B.id*c;
}
void solve()
{
	cin>>n>>c;
	vector<nood>ans;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		ans.push_back({x,i});
	}
	sort(ans.begin()+1,ans.end(),cmp);
	int flag=0;
	int sum=ans[0].w;
	for(int i=1;i<ans.size();i++)
	{
		if(ans[i].w+sum<ans[i].id*c)
		{
			flag=1;
			break;
		}
		sum+=ans[i].w;
	}
	if(flag==0)cout<<"Yes"<<endl;
	else cout<<"No"<<endl;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	int T=1;
	cin>>T;
	while(T--)solve();
	return 0;
}