单调栈完全解析

胡桃姓胡，蝴蝶也姓胡

已于 2022-09-13 06:14:45 修改

阅读量923

点赞数 4

分类专栏：数据结构与算法刷题文章标签：数据结构

于 2022-09-09 21:51:18 首次发布

本文链接：https://blog.csdn.net/qq_61039408/article/details/126788910

版权

数据结构与算法刷题专栏收录该内容

4 篇文章 0 订阅

订阅专栏

栈里面的元素存放数字下标组成的链表（有重复元素）

我们今天要讲解的数据结构是单调栈，单调栈顾名思义，使用的数据结构是栈Stack。单调栈中存放的数据具有一定的单调性，从而可以很好的求解一些问题。

单调栈的应用场景

假如我们有一个数组，我们有一个位置是i，我们需要得到比i位置小于等于或者大于等于的数字的左边和右边的坐标，而且这个坐标是离位置i最近的。此时我们需要得到数组的每一个位置的这样的信息。

使用单调栈，我们可以实现使用O(N)的复杂度求出这个信息。

例如我要找比3小的而且和3距离最近的左边和右边的坐标。因此我们就可以通过单调栈找出1和2。而且顺便的，我们可以遍历一次得到所有的下标的这个信息，这个就是单调栈的作用。

为什么要使用单调栈？

对于「找最近一个比当前值大/小」的问题，都可以使用单调栈来解决。

单调栈就是在栈的基础上维护一个栈内元素单调。

在理解单调栈之前，我们先回想一下「朴素解法」是如何解决这个问题的。

对于每个数而言，我们需要遍历其右边的数，直到找到比自身大的数，这是一个 O(n^2)的做法。

之所以是 O(n^2)，是因为每次找下一个最大值，我们是通过「主动」遍历来实现的。

而如果使用的是单调栈的话，可以做到 O(n)O(n) 的复杂度，我们将当前还没得到答案的下标暂存于栈内，从而实现「被动」更新答案。

也就是说，栈内存放的永远是还没更新答案的下标。

具体的做法是：

每次将当前遍历到的下标存入栈内，将当前下标存入栈内前，检查一下当前值是否能够作为栈内位置的答案（即成为栈内位置的「下一个更大的元素」），如果可以，则将栈内下标弹出。

如此一来，我们便实现了「被动」更新答案，同时由于我们的弹栈和出栈逻辑，决定了我们整个过程中栈内元素单调。

也就是说：

要从逻辑上去理解为什么能用「单调栈」解决问题：

我们希望将 O(n^2)算法优化为 O(n)算法，因此需要将「主动」获取答案转换为「被动」更新
我们需要使用数据结构保持那些「尚未更新」的位置下标，由于题目要求的是找「下一个更大的元素」，因此使用栈来保存
「被动」更新答案的逻辑导致了我们栈内元素单调

单调栈作用的基本过程

假设我们需要求比当前位置小的两个数字。

首先我们需要定义一个栈，这个栈由低向上存放的数据由小到大。

我们将数组的每一个元素的下标依次放入栈中。因为我们知道下标就可以通过下标找到值，而如果放值的话那么就无法定位到下标，因此需要用哈希表记录，这无疑是一种很大的浪费行为，因此我们应该放入下标作为单调栈的元素。例如：

我们先把1 放入栈中：

发现栈满足由小到大的规则，因此继续进行元素的存放。

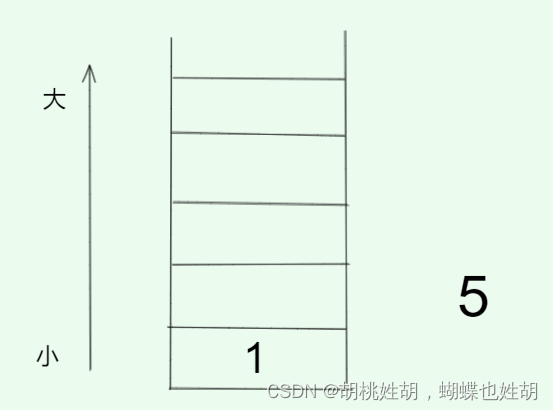
发现满足规则 1 < 5，于是我们可以把5放入栈中：

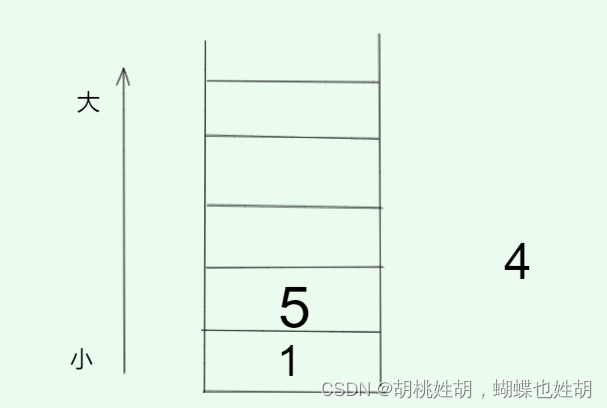
这个时候我们发现，4 < 5，不满足从小到大的元素要求了，于是我们不可以把4放入栈中，因为把4放入栈中就破坏了由小到大的规则。于是这个时候，我们应该把5弹出，此时压在5底下的1就是5这个数字左边的答案，没有压入栈的4就是5右边的答案。因为栈是从小到大递增的，所以5下面的就是左边的答案，而第一次出现的比5小的上面的4就是右边的答案，这个很容易想清楚。此时，我们已经求出了5的下标的左边和右边的数据了。

5出去之后发现1 < 4，所以可以把4压入栈中。

此时我们发现 4 > 3，所以3不可以压入栈中，把4弹出，4底下的1就是4的位置左边的答案的值，3就是右边的答案的值，此时，我们已经求出了值为4的左边和右边的答案了。

我们发现1 < 3，所以3可以压入栈中。

3 < 8，8可以压入栈中。

2 < 8，所以2不可以压入栈中，8弹出，8底下的3就是8左边的，2就是8右边的，此时我们已经求出了8的位置的答案了。

2 < 3，所以仍然不可以压入，3弹出，1是3左边的，2是3右边的，我们已经求出了3的位置的答案了。

1 < 2，可以压入。

2 < 9，可以压入。

9 > 4，4不可以压入，9弹出，2是9左边的，4是9右边的，此时我们已经求出了9的位置的答案了。

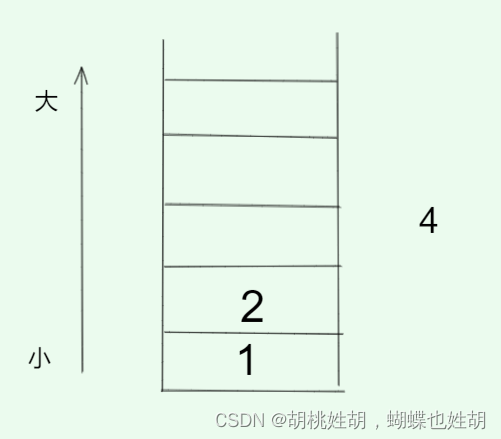
4可以压入。

2不可以压入，4弹出，2是4左边的，2是4右边的。此时我们已经求出了4的位置的答案了。

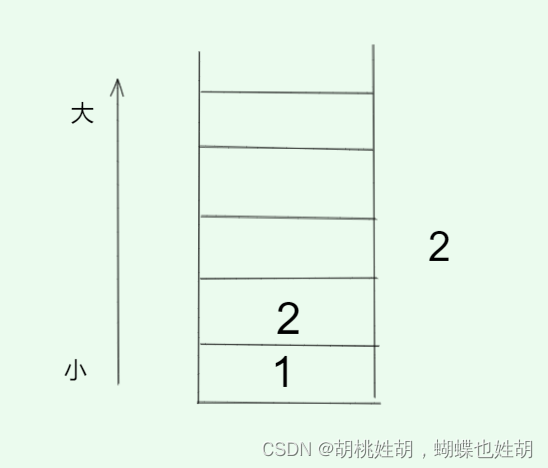
出现了相等的情况，我们这个时候认为不可以压入。

2弹出，1是2左边的，2是2右边的。

2可以压入。

0不可以压入，2弹出，得到2的位置的答案了。

不可以压入，1弹出，1底下没有数据，这说明1左边没有比它小的数字，0是1右边的答案。我们已经求出1位置的答案了。

0可以压入。

已经没有数字和我们再比较了，所以我们直接把0弹出，0下面没有数字，所以0左边没有比它小的，而0弹出之后数组为空了，所以0右边也没有比它小的数字。我们已经求出了0的位置的答案了。

可以看到我们求得答案的数字的顺序。可以发现不是顺序的，但是可以把所有的数字全部都求到答案。

单调栈的实现方式

我们用一个int[][] res 数组来记录位置和值左边和右边的下标。

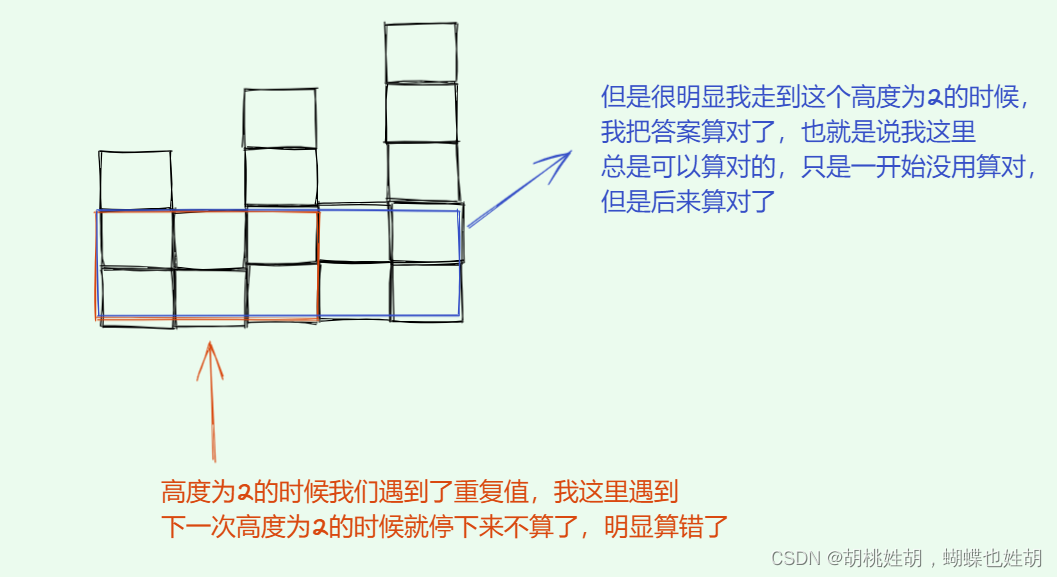
我们从上面的过程中可以知道，我们的数组可能会遇到重复的值，这个时候，我们依然要优先弹出，因为重复的值是具有连通性的，我第一个值算的结果可能不对，但是后面遇到重复的值的时候总可以算对。

i位置和j位置的值是重复的值，n和m是我需要的答案，假如我的i位置遇到了j就弹出了，那么确实算错了。

那么算到j的时候，我们也可以算出这个值的答案。这个性质在解题的时候很管用，因为单调栈的应用题不一定要精准的求出每一个位置的答案。但是如果我们硬是要求出每一个位置完全正确的值，放在数组里面的话，那么我们就需要用链表了。栈里面的元素不是一个下标，是下标组成的链表。

这里我们都用代码实现一下：

栈里面的元素存放数字下标（无重复元素）

public class MonotonousStack {
    public static int[][] getNearLessNoRepeat(int[] arr) {
        int[][] res = new int[arr.length][2];
        // 只存位置
        Stack<Integer> stack = new Stack<>();
        int N = arr.length;
        for (int i = 0; i < N; i++) {
            while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
                int j = stack.pop();
                int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
                res[j][0] = leftLessIndex;
                res[j][1] = i;
            }
            stack.push(i);
        }
        while (!stack.isEmpty()) { // 这个时候代表的是我的数字右边都一定没有比我小的，因为我在操作的过程中，每一个数字右边都没有值
            int j = stack.pop();
            int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
            res[j][0] = leftLessIndex;
            res[j][1] = -1; // 代表我右边没有值
        }
        return res;
    }
}

栈里面的元素存放数字下标组成的链表（有重复元素）

当我们遇到相同的元素的时候，就把相同的元素串联在链表后面。

当我们用链表的时候，我们每次弹出的值是链表的末尾的数字。并且一次性需要弹出一整条链表，具体道理大家可以自己思考一下，这个不难想象。

public class MonotonousStack {
    public static int[][] getNearLessNoRepeat(int[] arr) {
        int[][] res = new int[arr.length][2];
        // 只存位置
        Stack<List<Integer>> stack = new Stack<>();
        int N = arr.length;
        for (int i = 0; i < N; i++) {
            while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {
                List<Integer> pop = stack.pop(); // 这一条链表里面的所有的数字都应该被求出来了
                int leftNearIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
                for (Integer num : pop) {
                    res[num][0] = leftNearIndex;
                    res[num][1] = i;
                }
            }
            if (!stack.isEmpty() && arr[stack.peek().get(0)] == arr[i]) {
                stack.peek().add(Integer.valueOf(i));
            } else {
                List<Integer> list = new ArrayList<>();
                list.add(i);
                stack.push(list);
            }
        }
        while (!stack.isEmpty()) {
            List<Integer> pop = stack.pop();
            int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
            for (Integer num : pop) {
                res[num][0] = leftLessIndex;
                res[num][1] = -1;
            }
        }
        return res;
    }
}

单调栈的应用题目

直方图类型

这些题我是循序渐进的，所以一定要按照循序看才能体会到里面的精华。

题目一

给定一个非负数组arr，代表直方图返回直方图的最大长方形面积。

我们先来举一个例子，假如说我们有数组:

int[] arr = {3, 2, 4, 2, 5};

我们先画出代表这个数组的直方图。

接下来我们要求的是直方图的最大长方形面积。

我们来提取一下题目的信息：

长方形
最大

这两个信息是至关重要的。首先，我们需要保证是一个长方形，其次，我们要让这个长方形的面积达到最大。其实达到最大这一件事情是很简单的，我们只需要得到每一个长方形，然后求出面积，在求出面积的过程中，我们使用一个变量，maxValue来记录最大值就可以了。所以问题的关键其实是我如何在直方图中得到有效的长方形。

我们可以使用单调栈！

先说一下解题步骤，然后大家反过来思考为什么应该这么做：

我们有一个i位置，我们需要求出比i位置高度低的左边的离它最近的位置k和右边的离它最近的位置m。因为如果我的高度比i位置的高度高的话，那么我们是无法以i位置为高度构成一个长方体的。这里用单调栈求。
于是我们以i位置为高度就可以算出一个长方形的面积（m - i + 1 - 2）* i位置的高度。注意，这里是以i位置为高度求出对应的长方形的面积
遍历一遍，求出每一个位置的长方形的面积，并且求出他们当中最大的。

因此我们每次只需要求以某一个位置为高度的长方体面积就可以了。

    public static int largestRectangleArea(int[] height) {
        int maxArea = 0;
        Stack<Integer> stack = new Stack<>();
        int N = height.length;
        for (int i = 0; i < N; i++) {
            while (!stack.isEmpty() && height[stack.peek()] >= height[i]) {
                int j = stack.pop();
                int k = stack.isEmpty() ? -1 : stack.peek();
                int curArea = (i - k + 1 - 2) * height[j];
                maxArea = Math.max(maxArea, curArea);
            }
            stack.push(i);
        }
        while (!stack.isEmpty()) {
            int j = stack.pop();
            int k = stack.isEmpty() ? -1 : stack.peek();
            int curArea = (N - k + 1 - 2) * height[j];
            maxArea = Math.max(maxArea, curArea);
        }
        return maxArea;
    }

这里有一个小疑问，这个题目是很可能出现重复值的，为什么不用链表的形式串联起来？

答案是我们不需要串联起来，因为如果有重复值的话，我第一次遇到这个值可能会算错，但是后面会算对的，因为有重复值的时候具有连通性。

题目二

给定一共二维数组matrix，其中的值不是0就是1，返回全部由1组成的最大子矩形，内部有多少个1。

例如这个是我们的二维数组。

我们要求出里面的最大子矩阵内部有多少个1，说白了就是求最大子矩阵的面积。

我们做过题目一了，这道题和题目一一样是属于直方图类型的题目。

我们以第一行为基准可以生成一个直方图。

然后我们以第二行为基准也可以生成一个直方图。

我们生成的数组是2 2 2 2 0 2，这个数组可以画出一个直方图，那么这个数组是怎么生成的呢？

就是假如我是1就可以累加，是0的话就代表到达最大高度了，就不可以累加了。

第三行，第四行，第五行同理。

我们让每一行都生成一个直方图数组，然后我们的最大子矩阵的位置只有以下几种可能性。

最大子矩阵的位置在以第一行为基准的直方图里面。

最大子矩阵的位置在以第二行为基准的直方图里面。

最大子矩阵的位置在以第三行为基准的直方图里面。

。。。。。。

因为最大子矩阵一定在以某一行为基准的直方图里面，所以我们只需要把每一行为基准的直方图的最大矩阵面积全部都求出来就可以了。

    public static int maximalRectangle(char[][] map) {
        int maxArea = 0;
        int[] height = new int[map[0].length];
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[0].length; j++) {
                height[j] = map[i][j] == '0' ? 0 : height[j] + 1;
            }
            maxArea = Math.max(maxArea, maxRecFromBottom(height));
        }
        return maxArea;
    }

    private static int maxRecFromBottom(int[] height) {
        int maxArea = 0;
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < height.length; i++) {
            while (!stack.isEmpty() && height[stack.peek()] >= height[i]) {
                int j = stack.pop();
                int k = stack.isEmpty() ? -1 : stack.peek();
                int curArea = (i - k + 1 - 2) * height[j];
                maxArea = Math.max(maxArea, curArea);
            }
            stack.push(i);
        }
        while (!stack.isEmpty()) {
            int j = stack.pop();
            int k = stack.isEmpty() ? -1 : stack.peek();
            int curArea = (height.length - k + 1 - 2) * height[j];
            maxArea = Math.max(maxArea, curArea);
        }
        return maxArea;
    }

题目三

给定一个二维数组matrix，其中的值不是0就是1，返回全部由1组成的子矩阵的数量。

这道题也是直方图问题：

根据概率论的一些知识，我们可以很容易的得出一些答案：

子矩阵的数量 = 以第一排为基准的子矩阵的数量 + 以第二排为基准的子矩阵的数量 + 。。。。

于是问题转换成了，我们要求一个直方图里面的子矩阵的数量，这个怎么求呢？

例如我们有一块儿区域。

假如我要求高度为6的矩形的数量。这里我们限制死了，高度必须是6！那么我们可以根据等差数列求得，在这一块区域里面，高度为6的子矩阵数量是：

(N * (N + 1)) / 2

怎么来的？

我N，N ~ N + 1, N ~ N + 2, N ~ N + 3 ........ N ~ N + N可以构成矩形。有N个矩形

我N + 1, N + 1 ~ N + 2, N + 1 ~ N + 3.......N + 1 ~ N + N也可以构成矩形。有N - 1个矩形

。。。。有N - 2个矩形

。。。。

有1个矩形。

这很明显可以用到等差数列进行求解。

于是，我们成功求出了高度为6的，但是在这个区域里面还要高度为5的，高度为4的等等。这个区域里面的子矩阵和 = 高度为6的 + 高度为5的 + 高度为4的。。。。。

那么我们算到什么时候停止呢？

不符合规则的最近的左边的高度是4，右边是2，所以我们算到高度为4的时候就直接停止。因为我们高度为4的会由左边那个子矩阵的时候进行计算，如果我们这个时候进行计算了的话，就算重了。于是就是 :

(N + (N + 1)) / 2 * (height[cur] - Math.max(左边，右边))

那么这个时候还有一个很重要的问题：

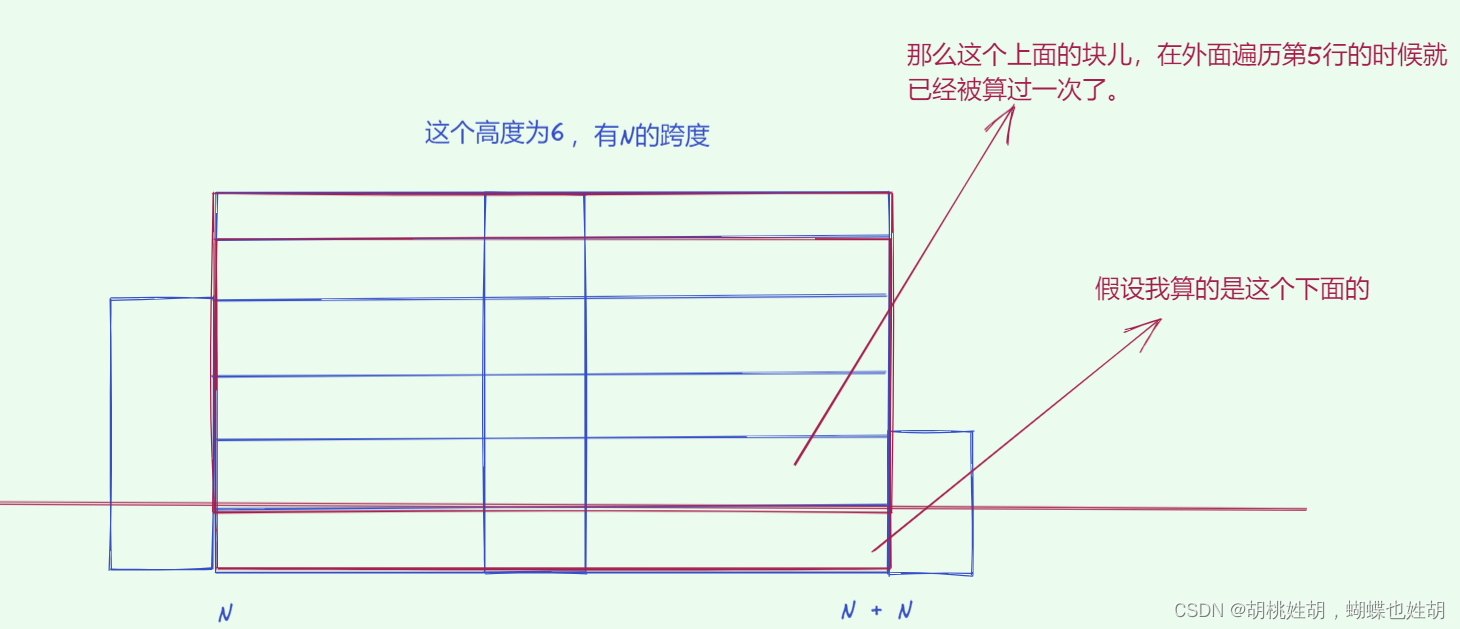
假如说我高度为5的子矩阵。

可以看到上面有，下面也有。但是我们的算法只能算到一边的。这样对吗。

答案是这样做没有问题，原因是：虽然我们这样只能算到下面的，也就是一边的，但是另外一边在遍历的时候一定会被算进去。例如：

    public static int num(int n) {
        return (((n + 1) * n) >> 1);
    }

    // 抽象成直方图
    public static int numSubmat(int[][] mat) {
        int nums = 0;
        int[] height = new int[mat[0].length];
        for (int i = 0; i < mat.length; i++) {
            for (int j = 0; j < mat[0].length; j++) {
                height[j] = mat[i][j] == 0 ? 0 : height[j] + 1;
            }
            nums += countFromBottom(height);
        }
        return nums;
    }

    private static int countFromBottom(int[] height) {
        int nums = 0;
        Stack<Integer> stack = new Stack<>();
        int N = height.length;
        for (int i = 0; i < N; i++) {
            // 这里注意，我们这里是不可以加等号的，因为我们加等号的话有一部分的区域会被计算两次
            while (!stack.isEmpty() && height[stack.peek()] > height[i]) {
                int j = stack.pop();
                int left = stack.isEmpty() ? -1 : stack.peek();
                // 算跨度
                int n = j - left + 1 - 2;
                // 算高度
                int down = height[j] - Math.max(left == -1 ? 0 : height[left], height[i]);
                nums += down * num(n);
            }
        }
        while (!stack.isEmpty()) {
            int j = stack.pop();
            int left = stack.isEmpty() ? -1 : stack.peek();
            // 算跨度
            int n = N - left + 1 - 2;
            // 算高度
            int down = height[j] - (left == -1 ? 0 : height[left]);
            nums += down * num(n);
        }
        return nums;
    }

直方图问题总结

形如子矩阵这样的问题，我们要解决此类问题有一个最大的约束，那就是保证这个图形是一个矩阵。单调栈可以做到这一点。而对于一个二维的空间来说，我们可以把一个二维空间压缩成很多个一维空间，每一个一维空间都可以使用单调栈求解。而二维空间的答案可以通过一维空间来求解。在这里可能需要一些概率论的知识，把一个大问题的求得得以分解成很多小的，可以分解成一维的问题来解决。

胡桃姓胡，蝴蝶也姓胡

关注

4
点赞
踩
4

收藏

觉得还不错? 一键收藏
打赏
0
评论
单调栈完全解析

形如子矩阵这样的问题，我们要解决此类问题有一个最大的约束，那就是保证这个图形是一个矩阵。单调栈可以做到这一点。而对于一个二维的空间来说，我们可以把一个二维空间压缩成很多个一维空间，每一个一维空间都可以使用单调栈求解。而二维空间的答案可以通过一维空间来求解。在这里可能需要一些概率论的知识，把一个大问题的求得得以分解成很多小的，可以分解成一维的问题来解决。
复制链接

扫一扫