0x17 二叉堆

0x17 二叉堆

二叉堆是一种支持插入、删除、查询最值的数据结构。它其实是一种满足“堆性质”的完全二叉树，树上的每一个节点带有一个权值。若树中的任意一个节点的权值都小于等于其父节点的权值，则称该二叉树满足“大根堆性质”，称其为“大根堆”。若树中的任意一个节点的权值都大于等于其父节点的权值，则称该二叉树满足“小根堆性质”，称其为“小根堆”。

根据完全二叉树性质，我们可以采取层次序列储存方式，直接用一个数组保存二叉堆。层次序列存储方式，就是逐层从左往右为树中的节点依次编号，把此编号作为节点在数组中储存的位置（下标）。在这种储存方式中，父节点编号等于子节点编号除以2，左子节点编号等于父节点编号乘2，右子节点编号等于父节点编号乘2加1，如下图所示：

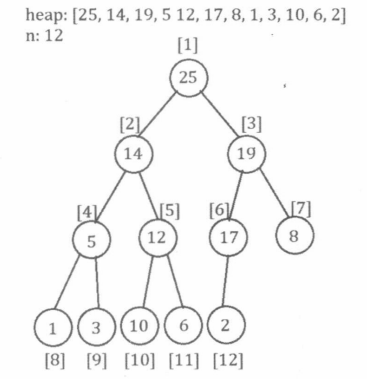
我们以大根堆为例，探讨堆支持的常见几种操作。

Insert:

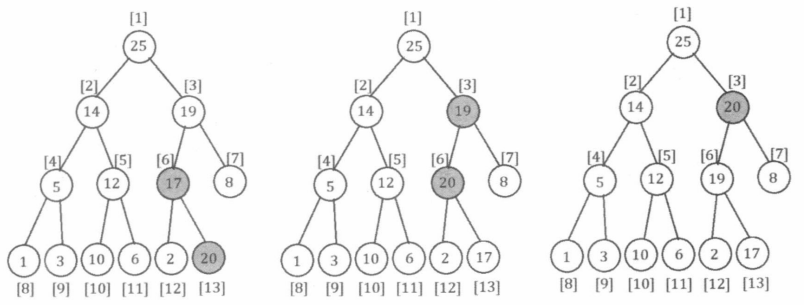
insert(val)操作向二叉堆中插入一个带有权值val的新节点。我们吧这个新节点直接放在储存二叉堆的数组末尾，然后通过交换的方式向上调整，直至满足堆性质。其时间复杂度为堆的深度，即$O(logN)$。

int heap[SIZE],n;
void up(int p) //向上调整
{
    while(p>1)
    {
        if(heap[p]>heap[p/2])
        {
            swap(heap[p],heap[p/2]);
            p/=2;
        }
        else
            break;
    }
}
void insert(int val)
{
    heap[++n]=val;
    up(n);
}

GetTop:

GetTop返回二叉堆的堆顶权值，即最大值heap[1]，时间复杂度为$O(1)$。

Extract:

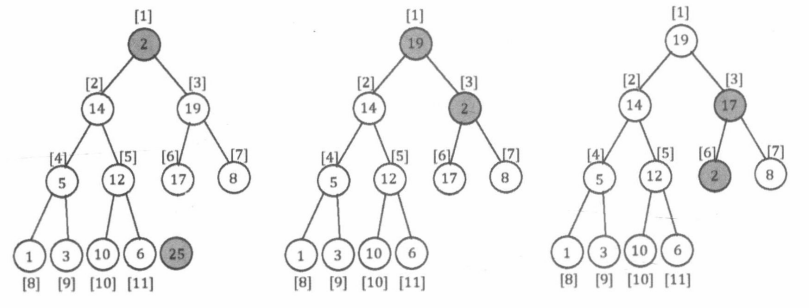
Extract操作把堆顶元素从二叉堆中移除。我们把堆顶heap[1]与储存数组末尾的节点heap[n]交换，然后移除数组末尾节点（令n减少1），最后把堆顶通过交换的方式向下调整，直至满足堆性质。其时间复杂度为堆的深度，即$O(logN)$。

void down(int p)
{
    int s=p*2; //p的左子节点
    while(s<=n)
    {
        if(s<n&&heap[s]<heap[s+1])
            s++;
        if(heap[s]>heap[p])
        {
            swap(heap[s],heap[p]);
            p=s,s=p*2;
        }
        else
            break;
    }
}

void Extract()
{
    heap[1]=heap[n--];
    down(1);
}

Remove:

Remove(p)操作把存储在数组下标p位置的节点从二叉堆中删除。与Extract相类似，我们把heap[p]与heap[n]交换，然后令n减少1。注意此时heap[p]既有可能需要向下调整，也有可能需要向上调整，需要分别检查和处理。时间复杂度为$O(logN)$。

void remove(int k)
{
    heap[k]=heap[n--];
    up(k),down(k);
}

C++ STL中的priority_queue（优先队列）为实现了一个大根堆，支持push(Insert)，top(GetTop)，pop(Extract)操作，不支持Remove操作，详细用法参见第0x71节。

1.Huffman树

考虑这样一个问题：构造一棵包含$n$个叶子结点的$k$叉树，其中第$i$个叶子结点带有权值$w_i$，要求最小化$\sum w_i\ast l_i$，其中$l_i$表示第$i$个叶子结点到根节点的距离。该问题被称为$k$叉Huffman树（哈夫曼树）。

为了最小化$\sum w_i\ast l_i$，应该让权值大的叶子结点的深度尽可能小。当$k=2$，我们很容易想到用下面这个贪心算法来求出二叉Huffman树。

1.建立一个小根堆，插入这$n$个叶子结点的权值。

2.从堆中取出最小的两个权值$w_1$和$w_2$，令$ans+=w_1+w_2$。

3.建立一个权值为$w_1+w_2$的树节点$p$，令$p$成为权值$w_1$和$w_2$的树节点的父亲。

4.在堆中插入权值$w_1+w_2$。

5.重复第2~4步，直至堆的大小为1。

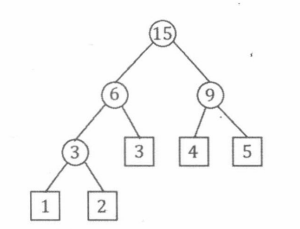
最后，由所有新建的$p$与原来的叶子结点构成的树就是Huffman树，变量ans就是$\sum w_i\ast l_i$的最小值。

对于$k(k>2)$叉Huffman树的求解，直观的想法是在上述贪心算法的基础上，改为每次从堆中取出最小的k个权值。然而仔细思考可以发现，如果在执行最后一轮循环时，堆的大小为$2\sim k-1$之间（不足以取出k个），那么整个Huffman树的根的子节点的个数就小于k。这显然不是最优解——我们任取Huffman树中一个深度最大的节点，把它改为根的子节点，就会使$\sum w_i\ast l_i$变小。

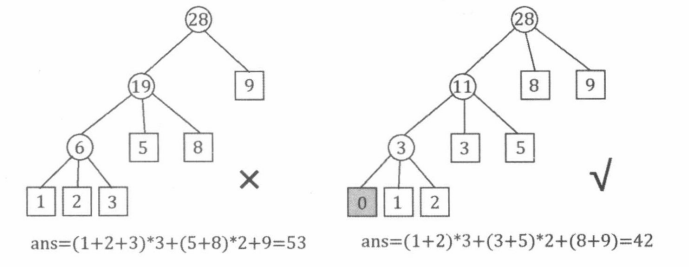
为此我们可以添加一些权值为0的叶子结点，使叶子结点的个数满足$(n-1)\mathrm{mod}(k-1)=0$，然后“每次从堆中取出最小的k个权值”的贪心想法就是正确的。