动态规划--背包系列

 

目录

 

1.01背包

2.完全背包

3.多重背包

4.分组背包

后续文章会给出例题！

 

 

---

 

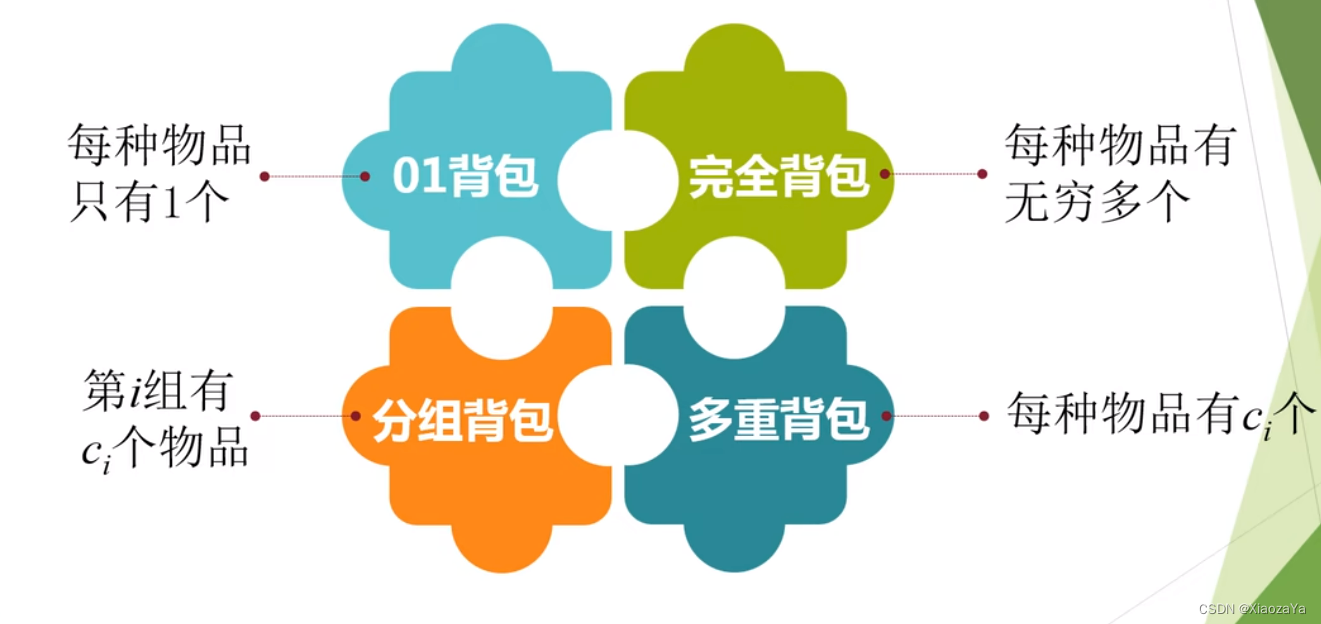
1.01背包

问题描述：

给定n个物品，每个物品仅有一个，其重量wi，价值vi，现有一容量为W的背包，求解：

在不超过背包容量的情况下，使放入背包的物品价值最大。

.1定义状态：dp[i][j]为将前i种物品放入容量为j的背包可以获得的最大价值

.2.确定状态转移方程：dp[i][j]=max(d[i-1][j-w[i]+v[i], dp[i-1][j])

解释：对于第i个物品有放(1)和不放(0)两种选择。

.3.确定边界值：由dp[i][j]的定义易知：dp[i][0]=d[0][j]=0

.4.模板代码

(该模板可以求出具体那些物品放入了背包)

int n, W;//n为物品种类数，W为背包容量
int dp[n+1][W+1];
//之后代码不在定义n, W, dp等变量
int bag(int w[], int v[]){
    for(int i=1;i<n+1;i++)
        for(int j=1;j<W+1;j++)
            if(j>=w[i]) dp[i][j]=max(dp[i-1][j-w[i]]+v[i], dp[i-1][j]);
            else dp[i][j]=dp[i-1][j];
    return dp[n][W];
}

//确认具体放入的物品
void find(int is_[],int w[]){
    for(int i=n,j=W,k=0;i>0;i--)
        if(dp[i][j]>dp[i-1][j]) is_[k++]=i,j-=w[i];
}

--空间优化

..1.滚动数组：

由状态转移方程知：dp[i][j]仅仅由dp[i-1][...]转移而来，即第i行的值只与第i-1行有关，因此仅需两行，一行用来保存(i)当前值，一行用来保存上一次(i-1)的值

int bag(int w[], int v[]){
    int dp[2][W+1]={0};
    for(int i=1;i<n+1;i++)
        for(int j=1;j<W+1;j++)
            if(j>=w[i]) dp[i%2][j]=max(dp[(i-1)%2][j-w[i]]+v[i], dp[(i-1)%2][j]);
            else dp[i%2][j]=dp[(i-1)%2][j];
    return dp[n%2][W];
}

..2.利用时间差倒推：

int bag(int w[], int v[]){
    int dp[W+1]={0};
    for(int i=1;i<n+1;i++)
        for(int j=W;j>=w[i];j--)
            dp[j]=max(dp[j-w[i]]+v[i], dp[j]);
    return dp[W];
}

2.完全背包

问题描述：

给定n个物品，每个物品有无数个，其重量wi，价值vi，现有一容量为W的背包，求解：

在不超过背包容量的情况下，使放入背包的物品价值最大。

与01背包基本一致，但注意一种物品在放入一个后，之后还可以继续放入

.1定义状态：dp[i][j]为将前i种(不是第i个)物品放入容量为j的背包可以获得的最大价值

.2.确定状态转移方程：dp[i][j]=max(d[i][j-w[i]+v[i], dp[i-1][j])

直接上优化代码：

...利用时间差正推：

这里对正推做简要解释：由状态转移方程知欲求dp[i][j]则需要先求出dp[i][j-w[i]]与dp[i-1][j]，而dp[i][j-w[i]]在dp[i][j]之前，所以正推先求出dp[i][j]之前的值----这里建议画图，清晰明了。

int bag(int w[], int v[]){
    int dp[W+1]={0};
    for(int i=1;i<n+1;i++)
        for(int j=w[i];j<=W;j++)
            dp[j]=max(dp[j-w[i]]+v[i], dp[j]);
    return dp[W];
}

3.多重背包

问题描述：

给定n个物品，每个物品仅有ci个，其重量wi，价值vi，现有一容量为W的背包，求解：

在不超过背包容量的情况下，使放入背包的物品价值最大。

.法1：暴力分解：

        将ci个种类相同的物品看成不同的物品，转换为01背包问题求解(容易TLE)

int bag(int w[], int v[], int c[]){
    int dp[W+1]={0};
    for(int i=1;i<n+1;i++)
        for(int k=1;k<=c[i];k++)
            for(int j=W;j>=w[i];j--)
                dp[j]=max(dp[j-w[i]]+v[i], dp[j]);
    return dp[W];
}

.法2：二进制拆分：

        

  为何选择二进制拆分，不选择三进制、四进制拆分？

       因为二进制拆分出来的数之间相互组合可以取满0~c[i]之间的所有物品且个数最少

       如上图将9拆分成1，2，4，2它们之间相互组合可以取到：0(一个都不要)、1、2、...、8、9

int bag(int w[], int v[], int c[]){
    for(int i=1;i<=n;i++)
        if(w[i]*c[i]>=W)
            //转换成完全背包 --- w[i]*c[i]>=W 意味着理论上i类物品的个数足够将背包装满
            for(j=w[i];j<=W;j++)
                d[j]=max(dp[j-w[i]]+v[i], dp[j]);
        else
            for(int k=1;c[i]>0;k<<1){
                //x是二进制拆分后的类包含的个数
                //eg:9 -- 1,2,4,2
                //k:1 2 4 8 --- c[i]:9 8 6 2 k与c[i]的同步变化
                //最后k会变成8 此时余量为c[i]=2所以取最小值
                int x=min(k, c[i]);
                //转换成01背包
                for(int j=W;j>=x*w[i];j--)
                    dp[j]=max(dp[j-x*w[i]]+x*v[i], dp[j]);
                //更新余量c[i]
                c[i]-=x; 
            }
}

若只是可信性，则可以使用数组优化。

4.分组背包

问题描述：

有 N 组物品和一个容量是 W 的背包。每组物品有若干个，同一组内的物品最多只能选一个。每件物品的体积是 wij，价值是 vij，其中 i 是组号，j 是组内编号。求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大，输出最大价值。

与01背包类似，但是每次选取则考虑组内最大

.1定义状态：dp[i][j]为将前i组物品放入容量为j的背包可以获得的最大价值

.2.确定状态转移方程：dp[i][j]=max(d[i-1][j-w[i][k]]+v[i][k], dp[i][j])

int bag(int w[][..], int v[][..], int cp[]){
    for(int i=1;i<=n;i++)
        for(int j=0;j<=W;j++)
            for(int k=1;k<=c[i];k++)
                if(j>=w[i][k])
                     dp[i][j]=max(dp[i-1][j-w[i][k]]+v[i][k], dp[i][j]);

     return dp[n][W];
}