Logisitic回归——房价预测-CSDN博客

本文链接：https://blog.csdn.net/qq_61676094/article/details/134630989

文章目录

前言
一、引用库
二、读取数据
三、sigmoid函数
四、梯度上升法
五、绘制数据点和回归直线
六、小小自我提问
总结

前言

啊每周写一篇真是让人热爱学习（bushi）

今天给大家带来的是线性回归中的一种经典方法——logistic（逻辑斯蒂）回归，并用该方法解决房价比例的问题

logistic回归——Logistic回归是统计学习中的经典分类方法，属于对数线性模型，所以也被称为对数几率回归。虽然是叫做回归，但其实这是一种分类算法，Logistic回归是一种线性分类器，针对的是线性可分问题。

利用logistic回归进行分类的主要思想是：根据现有的数据对分类边界线建立回归公式，以此进行分类。

一、引用库

绘图、矩阵计算

from matplotlib import pyplot as plt
import numpy as np

二、读取数据

这部分数据是进行了一些自我编写，数据量较少，但是将就能用。

再xsl中编写完成后另存为为txt格式进行读取

def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('xxhg.txt')   #同一文件夹相对地址mo问题
    for line in fr.readlines():                                       # 遍历读取数据
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])#一行三列矩阵
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat

三、sigmoid函数

逻辑回归作为分类算法，它的输出是0/1。那么如何将回归的一个输出值转换成0/1呢？

当当，此刻轮到我们sigmoid函数上场。

Sigmoid函数是一种常见的非线性函数，其数学表达式为1/(1+e^-x)。其中，x为自变量，e为自然对数的底数。Sigmoid函数的取值范围位于0到1之间。

$y=\frac{1}{1+e^{-x}}$

#绘制sigmoid函数
def draw():
    x = torch.linspace(-10,10,1000)
    y = 1/(1+torch.pow(math.e,-x))
    plt.plot(x.data.numpy(),y.data.numpy())
    plt.show()

sigmoid函数绘制：

设置sigmoid函数，将结果值映射到函数上可得到对应概率值

# sigmoid函数
def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))

四、梯度上升法

梯度上升法是一种迭代算法。其基本思想是通过不断调整参数来使目标函数的值不断增大，最终得到某函数的最大值。函数f（x,y）的梯度由下列式子表示：

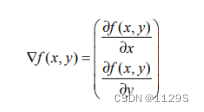
该梯度即分别按x和y方向移动对应函数（求微分）。其中，函数f(x,y) 必须要在待计算的点上有定义并且可微。

如图所示：

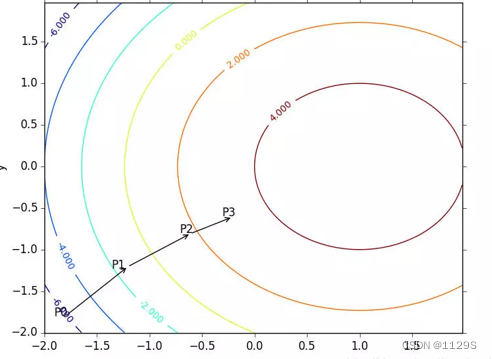
梯度上升算法到达每个点后都会重新估计移动的方向。从 P0 开始，计算完该点的梯度，函数就根据梯度移动到下一点 P1。在 P1 点，梯度再次被重新计算，并沿着新的梯度方向移动到 P2 。移动量大小为步长。如此循环迭代，直到满足停止条件（某个误差范围内）。迭代过程中，梯度算子总是保证我们能选取到最佳的移动方向。迭代公式：

$w:=w+\alpha \bigtriangledown _{w}^{}\textrm{f(w)}$

# 梯度上升算法
def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)                                    # 转换为NumPy矩阵
    labelMat = np.mat(classLabels).transpose()                        # 转换为NumPy矩阵，并且矩阵转置
    m, n = np.shape(dataMatrix)                                       # 获取数据集矩阵的大小，m为行数，n为列数
    alpha = 0.01                                                  # 目标移动的步长
    maxCycles = 500                                                # 迭代次数
    weights = np.ones((n, 1))                                         # 权重初始化为1
    for k in range(maxCycles):                                     # 重复矩阵运算
        h = sigmoid(dataMatrix * weights)                          # 矩阵相乘，计算sigmoid函数
        error = (labelMat - h)                                     # 计算误差
        weights = weights + alpha * dataMatrix.transpose() * error # 矩阵相乘，更新权重
    return weights

记得给标签矩阵转置！！！！！

计算出回归系数

dataMat, labelMat = loadDataSet()
weigths = gradAscent(dataMat, labelMat)
plotBestFit(weigths.getA())
print("w0: %f, w1: %f, W2: %f" % (weigths[0], weigths[1], weigths[2]))

五、绘制数据点和回归直线

def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()                      
    dataArr = np.array(dataMat)                               # 转换成umPy的数组
    n = np.shape(dataArr)[0]                                  
    xcord1 = []; ycord1 = []                               # 存放正样本
    xcord2 = []; ycord2 = []                               # 存放负样本
    for i in range(n):                                     
        if int(labelMat[i]) == 1:                          # 数据的标签为1，表示为正样本
            xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2])
        else:                                              
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=20, c='blue', marker='s')  # 绘制正样本
    ax.scatter(xcord2, ycord2, s=20, c='red')            # 绘制负样本
    x = np.arange(1.0, 10.0, 0.01)                             # x区间
    y = (-weights[0] - weights[1] * x) / weights[2]        # 最佳拟合直线
    ax.plot(x, y)
    plt.interactive(False)
    plt.title('分类结果')                                   # 标题
    plt.xlabel('房大小'); plt.ylabel('价格')                     # x，y轴的标签
    plt.show()

结果图：

六、小小自我提问

输入一个房子的大小和房子的价格，通过该回归函数得出该不该买这个房子呢？0是不买，1是买，sa！yikuzo！

用到了math.isclose进行判断需要额外加入一个math库~

#输入一个价位和房子大小 判断是否适合购买 适合输出1 不适合输出04
price=float(input("房子价位为："))
size=float(input("房子大小为："))
y=(-weigths[0] - weigths[1] * size) / weigths[2]
if math.isclose(price,y,rel_tol=0.7,abs_tol=0):#设置相对误差和绝对误差
    print("1")
else: print("0")