一个没啥大用，但好玩的东西

已于 2025-10-17 10:03:53 修改
阅读量364 收藏 6
点赞数 5
CC 4.0 BY-SA版权
分类专栏： 工具学习 文章标签： 服务器 运维
于 2025-10-15 12:06:41 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_61840254/article/details/153317251

DNS域名服务器解析与ip地址。之前一直搞不懂这个玩意儿，今天来好好探索一下。

概念：DNS(Domain Name System)是对网络/服务器的名字进行解析管理的系统。为什么要解析管理名字，是因为我们要通过名字（域名）进行计算机之间的相互访问。通过DNS把域名解析成IP地址来进行通信任务。ICANN管理全球域名、CNNIC管理中国域名

域名结构：主机名.三级域名.二级域名.顶级域名 
命名规则：字母数字连字符、不分大小写

例子：www.bilibili.com/主机 二级(权威域名) 顶级
           mail.163.com/主机 二级 顶级

解析域名的过程：查询一个网址www.bilibili.com

步骤 1：查询本地 DNS 缓存。用户在浏览器输入网址后，系统会先检查本地缓存。有ip返回，若本地缓存无记录或已过期，进入下一步。
步骤 2：查询本地 DNS 服务器。系统会向本地 DNS 服务器发送查询请求，这是用户网络默认配置的 DNS（如家庭网络由路由器分配，通常是运营商 DNS 或手动设置的公共 DNS，如 114.114.114.114）。有ip返回，若本地服务器无缓存，进入层级迭代查询。

步骤 3：查询根 DNS 服务器。本地 DNS 服务器向根 DNS 服务器（全球共 13 组，负责最高层级域名管理）发送请求，询问 “www.bilibili.com” 所属的顶级域名（.com）由哪个服务器管理。获得信息：“.com” 顶级域名的权威 DNS 服务器地址。
步骤 4：查询顶级域名（TLD）DNS 服务器。本地 DNS 服务器向 “.com”顶级域名 DNS 服务器发送请求，询问 “ bilibili.com ”（二级域名）的权威 DNS 服务器地址。获得信息：：“baidu.com” 的权威 DNS 服务器地址（即b站自己管理的 DNS 服务器）。
步骤 5：查询权威 DNS 服务器。本地 DNS 服务器向 “bilibili.com” 的权威 DNS 服务器发送请求，这是该域名的 “最终管理者”，存储着 “ www.bilibili.com ” 对应的 IP 地址。获得信息：IP地址。

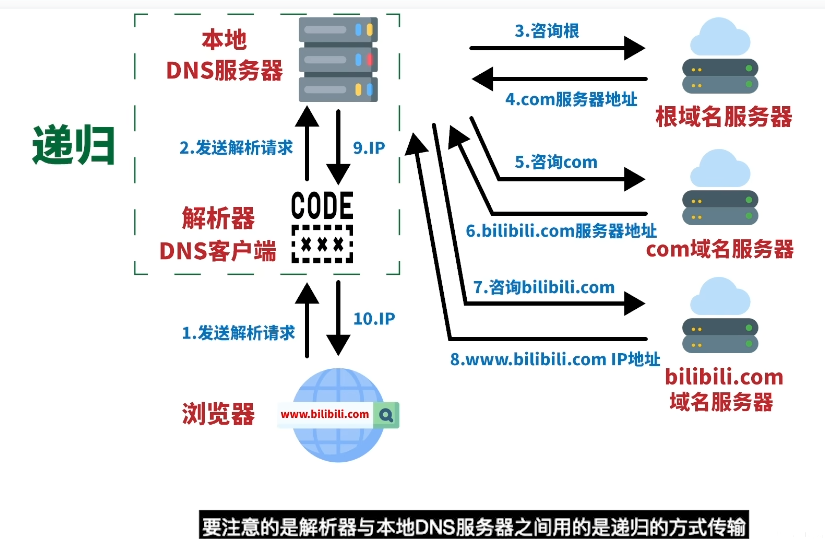
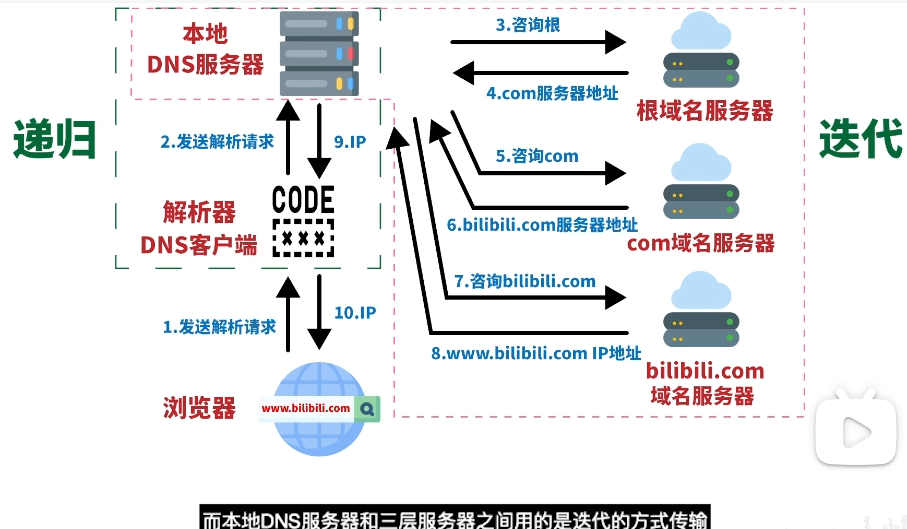
模拟本地 DNS 服务器的查询过程与解析

win+R——>cmd——>nslookup 域名

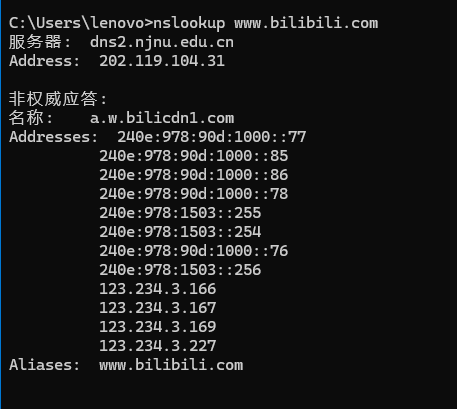
界面会先显示当前使用的 DNS 服务器地址，下方 “非权威应答” 后的内容即为解析结果，“名称” 对应主机名，“Addresses” 后列出的就是解析到的 IP 地址（可能包含 IPv4 和 IPv6）

那么实际上这就是全过程了，获得IP地址后，就可以正常上网或通信了。

毫无争议的github顶级有用的开源项目排行榜
github_35614077的博客
05-20 4952
github顶级有用的开源项目排行 TOP 14. 假装自己中病毒软件 https://github.com/bitdust/WamaCry 这个用途可太广泛了： 0. 一周没进展要开周会了怎么办 明天就是deadline了可是论文还没写完怎么办 这稿子还想再拖一周可是借口都用完了怎么办 不想加班，又找不到理由开溜怎么办 别人都中毒了，就我没中感觉out了怎么办 生活好无趣，想假装中毒发个朋友圈怎么办 ... ... TOP 13. 灭霸脚本 https://github.com/hotvulcan/
《白说》---- 读书笔记
浅语
01-23 3263
阅读日期：2017.01.10~2016.01.20说话不是件好玩的事儿（序）（1） 不是我说的话，安到我的头上，有麻烦也得替人担着；而真正是我说的话，常常麻烦也不少。（2） “做一个新闻评论员，最重要的素质是不是要有思想？”“不是。做一个称职的新闻评论员，最重要的是勇气，敏锐和方向感。”（3） “身在这里，还没走，守土有责；到点儿就撞钟，守时，可谓敬业；更重要的是，还得把日常的工作撞成自己与别人的
GCD介绍（一）: 基本概念和Dispatch Queue
wu347771769的专栏
06-05 368
什么是GCD？ Grand Central Dispatch或者GCD，是一套低层API，提供了一种新的方法来进行并发程序编写。从基本功能上讲，GCD有点像NSOperationQueue，他们都允许程序将任务切分为多个单一任务然后提交至工作队列来并发地或者串行地执行。GCD比之NSOpertionQueue更底层更高效，并且它不是Cocoa框架的一部分。 除了代码的平行执行能力，GC
【前端就业课 第一阶段】HTML5 零基础到实战（十）JavaScript基础一篇入门
1_bit 的博客
02-10 3527
注意：手机（APP）打开，内容显示更佳，不会的私聊博主即可 想要拿代码或加入学习计划（** 博主会监督你并且教你写文章 **）的拉到最下面（PC端Web打开）加博主即可，目录也在最下面。 参加1_bit博主前端学习计划发文时在头部记得加上本专栏链接，示例如下： 我已加入 1_bit 博主的免费前端 站起来 学习计划，专栏链接：https://blog.csdn.net/a757291228/category_11609526.html ...
计算机组成原理笔记——概论、数据表示、储存系统（王道考研）
亦梦亦醒乐逍遥的博客
06-11 3429
本文是对王道计算机考研《计算机组成原理》课程的总结，主讲咸鱼学长讲的确实清晰
从历史中讲创业的韧性
caoz的梦呓
12-03 450
又从知乎看到一个好玩的题目，说历史上意志力强大的例子，那么一个高票答案我也赞同，就是刘备刘皇叔。五次创业失败，四次妻离子散，关键几点第一，人家其实并非真的走投无路，从曹操...
JAVA零基础小白自学日志——第四天
mycqyjn的博客
07-02 710
今日学习，运算符
GCD
abcde459548764的博客
11-26 100
from：http://www.dreamingwish.com/dream-category/toturial/gcd-guide GCD介绍（一）: 基本概念和Dispatch Queue 什么是GCD？ Grand Central Dispatch或者GCD，是一套低层API，提供了一种新的方法来进行并发程序编写。从基本功能上讲，GCD有点像NSOperationQueue，...
第二十章
aohuang8877的博客
09-08 693
第二十章 唯与呵，其相去几何？美与恶，其相去何若？人之所畏，亦不可以不畏人。望呵，其未央哉！众人熙熙，若飨于太牢，而春登台。我泊焉未兆，若婴儿未咳。纍（léi）呵，如无所归。众人皆有余，而我独遗。我愚人之心也，沌沌呵。俗人昭昭，我独若昏。俗人察察，我独闷闷。沕呵，其若海。望呵，其若无所止。众人皆有以，我独顽以鄙。我欲独异于人，而贵食母。 第二十章1 人为啥会喜欢八卦新闻？ 各位朋友...
c代码-日常练习没啥大用
07-16
"C代码-日常练习没啥大用"这个标题虽然看似轻描淡写，但实际蕴含了学习编程的核心理念：通过日常练习来提升技能。无论对于初学者还是经验丰富的开发者，持续的实践都是至关重要的。 描述中的“没啥大用”可能是在...
在阿里云CentOS服务器上使用Certbot为Nginx配置SSL证书
Dxh0112_的博客
10-16 984
本文记录如何为阿里云CentOS服务器上的网站配置免费的Let's Encrypt SSL证书，解决浏览器“不安全”警告。
服务器连接百度网盘并下载文件
qq_58459892的博客
10-15 684
你可以去自己网盘主页刷新一下，确认能看到刚刚保存的那个文件夹以及里面的所有文件。：用我们已经验证过的命令行工具，从你自己的网盘里，把文件下载到服务器。：运行命令行工具，登录你的账号，把你网盘里的文件下载到服务器的数据盘。查看你网盘根目录的文件列表，找到第一部分里转存的那个文件夹的名字。：用浏览器，手动将分享链接的文件，转存到你自己的百度网盘里。”的流程，绕开了所有之前遇到的障碍，是目前最可靠的解决方案。：将别人分享的文件，变成你自己网盘里的“私有财产”。，也就是你要下载的、在你百度网盘里的那个文件夹。
开源 Linux 服务器与中间件（一）基本介绍
ajassi2000的博客
10-15 1422
本文记录了Linux C语言开发的学习历程，重点解析了Linux服务器与中间件的核心概念和应用场景。内容涵盖Web服务器（Nginx/Apache）、应用服务器（Tomcat/Node.js）、数据库（MySQL/Redis）及消息中间件（Kafka/RabbitMQ）等功能特点，并给出典型架构组合示例。通过对比不同技术的适用场景，帮助开发者构建高效稳定的系统架构。文章还附带C语言开发系列教程链接，为Linux开发学习提供完整参考路径。
云服务器与传统服务器租用的核心差异解析（云服务器与服务器租用之间的区别在哪里？）
本人是新手，有一定的了解不到位，望海涵
10-16 448
一般情况下，主要是对硬盘，CPU和内存进行升级，但服务器要考虑到软硬件的兼容问题，升级成本和难度也相对较高。云服务器和服务器租用其实与服务器托管是不一样的。从上述的情况综合而言，云服务器购置更灵活价格也会更低，在性能上面，虽然云服务器的技术让其完美解决了原来虚拟主机的不稳定的缺点，但是服务器租用的稳定性更胜一筹。服务器租用的稳定性和访问速度比较好，云服务器的访问速度很快，稳定性会比物理服务器差一点。但数据处理方面，高配置的服务器比云服务器相对更快，可以保证用户的访问响应速度，提升用户体验，性能也更稳定。
鲲鹏ARM服务器配置YUM源
Angushine的专栏
10-15 249
鲲鹏ARM服务器，安装的操作系统为CentOS7 2009。
在 Claude Code 中设置 MCP 服务器（技术总结）
qq_41586848的博客
10-15 1369
MCP（Model Context Protocol）是一种为Claude提供外部能力的机制，通过安装不同功能的MCP服务器，可赋予Claude文件系统访问、网页抓取、浏览器自动化等能力。文章详细介绍了各类MCP工具（如Sequential Thinking、Playwright、Brave Search等）的安装命令和配置方法，并提供了macOS/Linux的一键安装脚本。同时解释了不同系统下的配置文件位置差异、常见问题解决方案，以及如何通过结构化提示工程优化Claude使用MCP的效果。最后强调需注意全
上传OSS服务器图片文件视频(使用elemenplus上传组件)
lb2917的博客
10-16 1129
上传OSS服务器图片视频文件
HUAWEI A800I A2 aarch64架构服务器鲲鹏920开启虚拟化功能
最新发布
平庸
10-16 271
摘要 本文介绍了国产虚拟化配置中SMMU功能的开启步骤。SMMU作为硬件层面的内存管理单元，负责I/O设备与系统内存间的地址转换和安全隔离。配置流程包括：通过BMC控制台进入BIOS设置界面，在Advanced > MISC Config路径下依次启用"Smmu Work Around"和"Support Smmu"选项，最后保存设置并重启服务器使配置生效。该配置无需修改grub文件，适用于国产服务器虚拟化环境的初始化设置。
.NET UA Server SDK基于.NET Standard实现工业级OPC UA跨平台服务器
励志做最业余的专业博主，控件产品可以私我~
10-16 428
Unified Automation推出的.NET UA Server SDK是一款基于.NET Standard的专业开发工具包，旨在帮助开发者使用C#语言高效构建符合OPC UA标准的高性能服务器应用，实现跨平台部署与工业互联。
三个盒子一个里面有一百万选择了一个排除了一个选择的一个和没有排除的一个那个概率大用c语言表示
02-27
<think>嗯，用户的问题看起来是关于概率的，具体是三个盒子的选择问题。首先，我需要明确用户的问题到底是什么。他说的是三个盒子，其中一个有一百万，选择了一个之后排除了一个没有的，然后在剩下的两个中选择一个的概率问题。这让我想到可能是蒙提霍尔问题（Monty Hall problem），也就是常说的三门问题。 那用户的问题是不是这样：有三个盒子，其中一个有百万奖金，参赛者选择一个后，主持人会打开一个没有奖金的盒子，然后问参赛者是否要换剩下的那个盒子，这时候换的概率更高？如果是这样的话，那么正确的概率应该是换的话有2/3的概率中奖，不换的话是1/3。所以用户可能是在问这个情况下的概率差异，并且希望用C语言来表示或者验证这个概率。 不过用户提到“用C语言表示”，可能需要用程序来模拟这个过程，通过大量的试验次数来验证概率是否正确。所以接下来我需要考虑如何用C语言编写一个模拟程序，模拟多次选择，分别计算换与不换的中奖概率。 首先，我需要明确步骤。程序的大致思路应该是： 1. 初始化三个盒子，随机放置百万奖金。 2. 参赛者随机选择一个盒子。 3. 主持人打开一个没有被选中且没有奖金的盒子。 4. 参赛者选择是否更换到剩下的那个盒子。 5. 记录换与不换的中奖情况。 6. 重复多次，统计概率。 然后，需要处理一些细节问题，比如如何随机生成奖金的盒子，如何选择主持人打开的盒子，以及在换与不换时的判断逻辑。比如，当参赛者初始选择正确的情况下，主持人会随机打开另外两个中的一个，这时候如果换就会输；如果初始选择错误，主持人只能打开剩下的那个没有奖金的盒子，换的话就会赢。所以在程序中需要正确模拟这些情况。 接下来，我需要考虑如何用C语言实现这些步骤。可能需要使用随机数生成函数，比如srand和rand，但要注意设置随机种子，比如用time(NULL)来初始化。然后，用循环来进行多次试验，比如十万次或者一百万次，记录换和不换的成功次数。 可能的代码结构如下： - 包含头文件：stdio.h, stdlib.h, time.h。 - 主函数中设置随机种子。 - 定义变量，比如试验次数、换的成功次数、不换的成功次数。 - 循环试验次数次： - 随机生成有奖的盒子（0、1、2中的一个）。 - 参赛者随机选择一个盒子（0、1、2中的一个）。 - 确定主持人要打开的盒子：从剩下的两个盒子中排除有奖的那个，如果参赛者选对了，主持人随机选剩下的两个中的一个；如果参赛者选错了，主持人只能选剩下的那个没奖的。 - 确定剩下的盒子（换的话就是剩下的未被打开和未被选择的那个）。 - 判断换是否中奖，以及不换是否中奖，统计次数。 - 最后计算概率并输出。 不过，这里可能有个问题，当参赛者初始选择正确时，主持人有两个盒子可以打开，这时候在程序中需要随机选择一个。但如果是这样的情况，是否会影响概率？根据蒙提霍尔问题，换的概率是2/3，无论主持人如何选择。所以即使主持人随机选，换的概率仍然应该是2/3。所以在程序中需要正确处理这种情况。 另外，在代码实现时，如何确定主持人打开的盒子？比如，假设奖在prize_box，参赛者选的是choice。剩下的两个盒子是另外两个，主持人必须打开一个没有奖的。如果参赛者的选择正确（choice == prize_box），那么主持人可以在剩下的两个盒子中任选一个；如果参赛者的选择错误，那么主持人必须打开剩下的那个没奖的盒子。 例如，假设盒子是0、1、2。prize_box是随机生成的。参赛者选的是choice。然后主持人需要从剩下的两个盒子中排除有奖的，并打开一个没有奖的。剩下的那个未被打开和未被选择的盒子就是换的选项。 所以，在代码中，可以这样处理： 当参赛者选择后，遍历所有盒子，找到不是choice且不是prize_box的盒子，这些就是主持人可以打开的盒子。如果参赛者选对了，那么有两个盒子可选，主持人随机选一个；如果选错了，那么只有一个盒子可以打开。 或者另一种方法：主持人必须打开一个不是参赛者选择且没有奖的盒子。剩下的那个未被打开的盒子就是换的选项。 例如： 确定所有可能的盒子，然后主持人打开其中一个符合条件的盒子，剩下的那个就是换的选项。 具体到代码，可能需要列出所有可能的盒子，然后找出哪些可以作为主持人打开的盒子，再随机选一个，或者唯一的一个。 例如，假设prize_box是0，参赛者选0，那么主持人可以打开1或2中的一个；如果参赛者选1，而prize_box是0，那么主持人必须打开2。 所以在代码中，可以用循环来找主持人可以打开的盒子： for(int i=0; i<3; i++){ if(i != choice && i != prize_box){ // 这个i是主持人可以打开的盒子 host_open = i; // 如果有多个，随机选一个 } } 不过，这样可能只能找到一个，如果有多个的话，比如参赛者选的是prize_box时，可能会有两个选项。这时候需要收集所有可能的选项，然后随机选一个。 所以，正确的做法是，生成一个数组，包含所有可能的可以被主持人打开的盒子（即不是参赛者的选择，且不是有奖的），然后从中随机选一个。如果这个数组的长度是1，直接选；如果是2，随机选一个。 例如： int available_doors[2]; int count = 0; for(int i=0; i<3; i++){ if(i != choice && i != prize_box){ available_doors[count] = i; count++; } } // 然后从available_doors中随机选一个，即0到count-1的索引 int host_open = available_doors[rand() % count]; 然后，剩下的盒子就是剩下的那个未被choice和host_open选中的盒子。这时候换的盒子就是剩下的那个。 例如： 剩下的盒子是0,1,2中，不是choice也不是host_open的那个。即： int remaining; for(int i=0; i<3; i++){ if(i != choice && i != host_open){ remaining = i; break; } } 然后，换的话就是选择remaining，不换的话就是原来的choice。 然后比较remaining是否等于prize_box，以及choice是否等于prize_box，来统计换和不换的成功次数。 所以整个程序的逻辑大致是这样。然后，通过大量的试验次数，比如一百万次，统计换的成功次数除以总次数，应该接近2/3，不换的成功次数接近1/3。 现在，用户可能希望看到这样的C代码，以及相应的解释。所以，在回答中需要先解释问题的背景，即蒙提霍尔问题，然后给出C代码的示例，模拟这个过程，最后说明运行结果及其概率。 不过，用户的问题描述可能有些不太准确，比如“排除了一个选择的一个和没有排除的一个那个概率大”，需要确认是否是蒙提霍尔问题。所以，在回答的开始部分，需要先确认问题，并解释正确的概率模型，然后用C代码来验证。 此外，用户可能对概率的计算不太清楚，所以需要用代码来直观展示。同时，代码需要正确无误，能够正确模拟主持人开门的过程，并正确统计换与不换的成功率。 综上，我应该首先解释蒙提霍尔问题的基本情况，然后给出C语言的实现代码，并说明代码的逻辑，最后指出运行结果会显示换盒子的成功率更高，约为2/3，而不换的为1/3。</think>这个问题描述的是经典的**蒙提霍尔问题**（三门问题），以下是分析及C语言模拟： --- ### 问题分析 1. **场景**：3个盒子（0、1、2），1个有奖，参赛者选1个后，主持人会打开1个无奖的盒子，问是否要换选剩下的盒子。 2. **概率**： - **不换**：初始选中奖盒的概率为 **1/3**。 - **换**：若初始选错（概率2/3），换必中奖。因此换的中奖概率为 **2/3**。 --- ### C语言模拟代码 ```c #include <stdio.h> #include <stdlib.h> #include <time.h> int main() { srand(time(NULL)); // 初始化随机种子 const int TRIALS = 1000000; // 模拟次数 int stay_wins = 0, switch_wins = 0; for (int i = 0; i < TRIALS; i++) { int prize = rand() % 3; // 随机生成有奖的盒子 int choice = rand() % 3; // 参赛者随机选择一个盒子 // 主持人打开一个无奖且未被选择的盒子 int host_open; do { host_open = rand() % 3; } while (host_open == prize || host_open == choice); // 剩下的盒子是换的选择 int remaining; for (remaining = 0; remaining < 3; remaining++) { if (remaining != choice && remaining != host_open) break; } // 统计结果 if (choice == prize) stay_wins++; if (remaining == prize) switch_wins++; } printf("不换的中奖概率: %.2f%%\n", (stay_wins / (double)TRIALS) * 100); printf("换的中奖概率: %.2f%%\n", (switch_wins / (double)TRIALS) * 100); return 0; } ``` --- ### 运行结果示例 ``` 不换的中奖概率: 33.34% 换的中奖概率: 66.66% ``` --- ### 结论 - **换盒子**的中奖概率（约66.67%）显著高于**不换**（约33.33%）。 - 程序通过模拟百万次试验验证了这一概率。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值