【论文研读】基于图傅里叶变换的音频零水印

本文链接：https://blog.csdn.net/qq_61879501/article/details/134317153

发表于IEEE Signal Process 影响因子3.9

摘要

当今时代多媒体信息的频繁交换，对版权保护提出了越来越高的要求。在这项工作中，我们提出了一种新的基于图傅立叶变换的音频零水印技术，以增强版权保护方面的鲁棒性。在这种方法中，使用组合移位算子来构造图信号，在该图信号上执行图傅立叶分析。然后使用K-means算法将所选择的表示音频片段的特性的最大绝对图傅立叶系数编码为特征二进制序列。最后，将得到的特征二进制序列与水印二进制序列进行异或，实现零水印的嵌入。实验研究表明，与现有技术相比，所提出的方法在抵御常见或同步攻击方面表现得更有效。
关键词：音频水印、图信号处理、图傅立叶变换、同步攻击

1.技术背景

互联网和多媒体技术的飞速发展使多媒体信息的交流达到了前所未有的深度。然而，与此同时，盗版和篡改也变得猖獗。数字水印技术是其解决方案之一，近年来受到广泛关注。
音频零水印技术由于其优异的隐蔽性，是一种很有前途的音频版权保护技术，同时也有可能提高其鲁棒性。零水印技术不修改主机音频信号的数据，而是根据其内容特征构建水印信息。

基于探索稳定内容特征的不同技术，音频零水印可以大致分为两类：时域矢量映射和变换域方法。

通常，奇异值分解（SVD）用于寻求基于时域的稳定特性。采用具有稳定性的最大奇异值来表示音频特征，音频内容的重复性使基于SVD的零水印方法能够有效抵御严重的同步攻击。
基于变换域的水印技术，包括离散余弦变换（DCT）、离散小波变换（DWT）、傅立叶变换（FT）和线性预测倒谱系数（LPCC）。具体而言，基于DCT域的技术将DCT应用于主机音频信号，以获得一组音频片段。然而，这些技术创新在于音频片段特征的选择。基于DWT域的技术类似于DCT方法，后者对主信号执行DWT以选择音频片段的稳定特性。此外，基于FT的相位信息也通常用于表征音频片段的特性。

基于幅度信息——如DCT、DWT或多个变换域的组合来表征音频片段特征的技术可以有效抵御常见的攻击（如噪声、滤波和重采样攻击等），而它们通常不具备抵御苛刻同步攻击的能力（如时标修改（TSM），裁剪攻击）。相反，基于FT相位信息的技术比基于幅度信息的技术更能抵御同步攻击。然而，它们并不能很有效地抵御常见的攻击。

2.引入

为了进一步增强对各种攻击的鲁棒性，本文提出了一种新的基于图傅立叶变换（GFT）的音频零水印技术。
新兴的图信号处理（GSP）技术已被用于语音处理，以表达语音样本数据点的结构关系。由数据点之间的势关系构建的图拓扑可以确定图傅立叶基，GFT可以进一步分析图信号在图频域中的特性。在使用GFT对非结构化数据（如点云和图数据）进行水印方面取得了进展。
在这里，我们采用GFT将语音信号从图域转换到图频域，以稳定音频片段的特性。然后，我们对所有选择的图傅立叶系数进行编码，这些傅立叶系数可以表征音频片段，以实现零水印嵌入。我们针对各种方法对我们提出的方法进行了评估，以显示对常见攻击和同步攻击的有效性。

3.音频信号的频谱图

在本节中，我们描述了将时域中的音频信号映射到图域的过程，然后描述了将图信号转换到图频域的细节，以进一步分析其特性。

3.1 音频信号的图域映射

图信号的基本概念：为了将时域中的音频信号x映射到图域中的图形音频信号y，有必要利用GSP中的图形。图由顶点、连接顶点的边和边权重组成。数学上，图可以表示为，G=（V，E，W），其中V表示顶点集，E表示边集，W表示权重集。
为了利用GSP来处理音频信号，首先将时域信号x划分为多个帧，然后对每个帧进行映射。假设x被划分为具有N个采样点的M个帧，其中一个帧可以表示为xm=[xm1，xm2，…，xmN]^T，并且m=1，2。。。，M。给定一个图，ym可以表示为一个图信号，它被定义为如下映射。
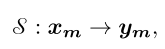
在这里插入图片描述
其中，由G=（V，E，W）索引的ym=[ym1，ym2，…，ymN]^T是xm的一对一映射值。ym的每个元素表示对应图中顶点处的强度，每个顶点对应于时域中的采样点。对应的图G描述了顶点之间的关系，并且可以如下等式中给出的那样详细地书写。
在这里插入图片描述
这里，eij=0表示顶点vi和vj之间不存在边连接，否则eij=1。wij表示vi和vj之间的边的权重。一般权重矩阵可以用图拉普拉斯矩阵L或图邻接矩阵A来表示。其中，L只适用于无向图，而A不适用于。考虑到语音信号是一个具有明显时间相关性的时间序列，定向权值可以准确地表示语音时间采样点之间的关系。因此，这项工作采用A作为W，A的元素值为0或1，以达到只关注顶点之间是否存在连接的目的。

图音频信号的构造：在这项工作中，使用组合图k移算子Γk来构造A，以获得图语音信号。根据上面的分析，A等价于W和E作为一个二元矩阵，图可以重新定义为GΓk=（V，Γk，Γk）。Γk定义为
在这里插入图片描述
其中γt∈R^N×N（t=0，1，…，）是一个二进制矩阵，它表示一个t移位算子。Γk的元素γij满足以下条件

显然，当k=1时，Γ1=γ0是一个单位矩阵，这意味着信号没有移位。在时域信号yi上实现Γk后得到的图信号yo可以表示为yo=Γk·yi。

3.2 音频信号在图形频域中的频谱

借助邻接矩阵A，将图域信号转换为图频域信号。具体方法对A进行奇异值分解，得到A的奇异值分解，A = QΣQ⁻¹，其中Q = [ε1， ε2，…]， εN]∈R^N×N由A和Σ的N特征向量组成，ζ1， ζ2，…， ζN]∈R^N×N, N特征向量作为a的主对角线，Q的εt表示对应图频率ζt处的谱分量。
由于这里的A是具有全行秩的行梯形矩阵，这将导致N个线性独立的特征向量。相应地，Q是可逆的，图傅立叶矩阵F可以定义如下。
在这里插入图片描述
在对图形信号y执行GFT之后获得的图形频谱y~可以表示为

其中y~ft表示相应图形频率ζt下的图形傅立叶系数。此外，结合以上两个等式注意到，GFT本质上是一个简单的矩阵运算过程，并且它是一种没有延迟的方法。

4.一种基于GFT的音频零水印算法

所提出的框架在GFT域中执行零水印处理。图1显示了零水印生成和提取过程的流程图。零水印的嵌入和提取有一些常见的过程，包括成帧、构造图信号、GFT和编码。我们注意到他们的XOR过程略有不同。
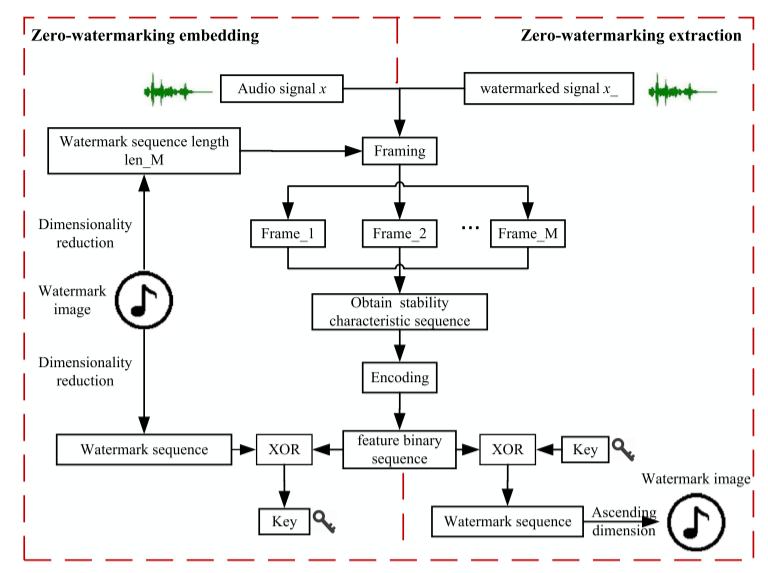
在这里插入图片描述
图1：提出的零水印方案：左：零水印嵌入；右图：零水印提取。

常规流程

成帧：根据水印图像降维得到的水印序列的长度M，将音频信号x均匀划分为M个不重叠的帧。每个帧的长度由N表示。因此，我们有N＝floor（x_len/M），其中x_len表示音频信号x的长度。
构造图信号：一旦时域信号被帧化，其中一个帧可以表示为x（m）=[x1^（m），x2^（m）…，xN^（m）]T，并且m＝1，2。。。，M。通过在x^（M）上执行组合图k移算子Γk，我们可以获得图信号y^（m）。
GFT：在Γk上应用SVD的基础上，可以得到GFT基FΓk。然后可以通过下面公式获得图信号y^（m）的图频谱系数y~Γk。

考虑到图形频谱主要集中在较低的频率，并且当k小时，频谱相对稳定。此外，较大的k将导致较高的计算量。在这项工作中，我们主要讨论当k=3时的情况。
编码：为了获得音频片段的稳定性特征序列，我们分析了持续时间为22秒的音频中片段的最大频谱系数的绝对值。图2显示了1024帧中前256帧在不同攻击下的最大绝对图谱系数值。从图2中可以清楚地观察到，在这些攻击之后，这些值发生了一些变化，但趋势相对稳定。因此，这些值可以用来表示每个帧的特征序列F以抵抗攻击。
为了获得每个音频片段的特征二进制序列B，使用K-means聚类算法将特征序列F分为两类，分别编码为0和1。

在这里插入图片描述
图2：不同攻击下的最大绝对图谱系数值。

不同的过程

零水印嵌入异或：将得到的信号特征二进制序列与水印序列异或，得到水印密钥K，如下所示。其中W（m）是二进制图像的像素点值。
零水印提取的异或：水印信号特征二进制序列B’ 与水印密钥K异或，得到水印序列W’，如下所示。

最后，可以通过增加维数将获得的水印二进制序列恢复为水印图像，如图3所示。

图3：所提出的方案在攻击下提取的水印图像：（a）原始图像；（b） AWGN（10dB）；（c） olph；（d）重新取样；（e） MP3；（f）重新量化；（g）振幅（2倍）；（h） TSM 1%；（i） TSM 10%；（j） TSM-1%；（k） TSM-10%；（l）裁剪5帧（前）；（m）裁剪10帧（正面）；（n）裁剪20帧（前）

5.实验结果及分析

5.1 实验设置

数据库：为了验证所提出的零水印方案的有效性，从DSD100数据库中随机选择了各种风格的音频片段，包括摇滚、古典、爵士、乡村和流行音乐。总共有40首音乐，每个音频剪辑的持续时间为64秒，以44.1kHz采样并用16位量化。采用大小为64×64的二进制图像生成零水印，如图所示。第3（a）段。
性能指标：在这项工作中，分别使用误码率（BER）和归一化互相关系数（NC）来评估所提出方案的可靠性并衡量其抗攻击能力。在评估稳健性时，经常使用以下常见攻击和同步攻击。

常见攻击

AWGN（加性高斯白噪声）：AWGN的信噪比分别为10dB和20dB。
LPF（低通滤波器）：水印信号通过截止频率为11025Hz的低通滤波器进行滤波。
重新采样：将采样频率更改为22.05kHz，然后重新采样为44.1kHz。
重新量化：位数从16位减少到8位，然后从8位增加到16位。
MP3：水印信号以MP3格式（128kbps）进行压缩。
振幅：水印信号的振幅分别放大1.5倍和2倍。

同步攻击

TSM（时间刻度修改）：修改水印信号的时间刻度。
裁剪：水印信号的正面或背面被裁剪几帧。

5.2 常见攻击下的性能比较

表I显示了在常见攻击下，所提出的方案与基线之间的性能比较。
在这里插入图片描述
表I：在常见攻击下，所提出的方案和基线的稳健性比较，其中**/**表示平均指标BER/NC，粗体标记表示在每次攻击下所有方案的最佳数字。

我们观察到，在振幅攻击下，所提出的方案和前四个方案都可以有效地提取水印比特，而[19]中提出的方案无法抵抗振幅攻击。此外，所提出的方案在前六种攻击下的鲁棒性与方案[19]一样优越，但明显优于基于其他三个变换域的方案。这一结果背后的原因可能归因于稳健的图傅立叶系数和使用K均值对特征序列进行聚类以获得特征二进制序列。
总体而言，所提出的方案在抵御常见攻击方面具有出色的性能，并且优于基线。此外，位于图3第一行的水印图像是在主机信号受到常见攻击后提取的。提取的图像看起来与原始图像几乎相同，这说明了所提出方法的稳健性。

5.3 同步攻击下的性能比较

表II显示了在同步攻击下，所提出的方案与基线之间的性能比较。可以观察到，随着TSM的变化越来越大，所提出的方案的鲁棒性降低。在裁剪攻击下也可以发现这种趋势，并且所提出的方案的鲁棒性随着裁剪帧数量的增加而降低。这种趋势背后的原因可以通过水印提取过程来解释。由于水印被顺序嵌入主机音频信号中，并且主机信号受到TSM和裁剪攻击，因此相应音频片段的特性可能不合适，这将影响水印的正确提取。在图3的第二行中，在同步攻击下提取的水印图像都有轻微的乱码，这在更严重的攻击情况下更为明显。然而，要注意的是，仍然可以获得水印图像的有意义的信息。此外，与基线相比，该方案在TSM和裁剪攻击下具有更好的鲁棒性。这可能与鲁棒图傅立叶系数和使用K均值对特征序列进行聚类以获得特征二进制序列有关。
在这里插入图片描述
表II：在同步攻击下，所提出的方案和基线的鲁棒性比较，其中**/**表示平均指标BER/NC，粗体标记表示在每次攻击下所有方案的最佳数字。