目录
在学些图的基本算法之前,咱们一般得掌握一些图的基本知识,比如说什么是图,图的种类等。而这篇博客主要是对学习图的一些基础算法前,对图的一些基本介绍。准备好,那咱们就开始咯。
一、图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成的,通常表示为G(V, E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
若V ={V,V
,...,V
} ,则用 |V| 表示图G中顶点个数,E = {(u, v) | u
V, v
V},用 |E|表示图G中边的条数。
注:图不可以是空图。即图中不能一个顶点也没有,图的顶点集 V一定非空,但是边集 E可以为空,此时图中只有顶点而没有边。
(1)无向图
无向边:若顶点V
到 V
之间的边没有方向,则称这条边为无向边(Edge) ,无序偶对
( V
,V
)来表示。对于无向对,其表示的边的顶点顺序可以是任意的,比如边(1,2)也可以用边(2,1)表示。
无向图:如果图中任意两个顶点之间的边都是无向边,则称该图为无向图(undirected graphs) 。
对于下面的无向图G来说,G = (V, {E}) ,其中顶点集合 V = {V,V
,V
,V
};边集合E = {(V
,V
),(V
, V
),(V
,V
),(V
,V
),(V
,V
)}。
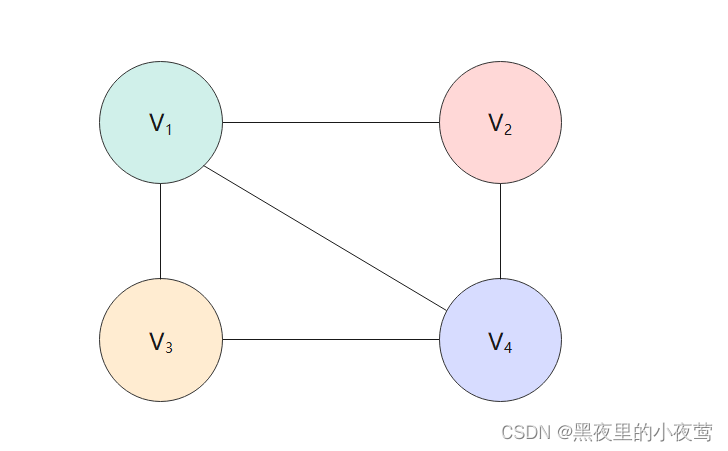
对于无向图 G = (V, {E}),如果边 (V, V
}
E,则称顶点 V
和 V
互为邻接点(Adjacent),即 V
和 V
相邻接。顶点 v 的度(Degree)是和 v 相关联的边的数目,记为TD(v)。
上图中,V 的度为 3,V
的度为 2,其他顶点以此类推。
对于具有n个顶点、e条边的无向图,
TD(V
) = 2e,即无向图的全部顶点的度的和等于边数的2倍,因为每条边和两个顶点相关联。
(2)有向图
有向边:若顶点V
到 V
之间的边有方向,则称这条边为有向边,也称为弧(Arc)。用有序偶对<V
,V
>来表示,V
称为尾弧(Tail),V
称为弧头(Head)。
有向图:如果图中任意两个顶点之间的边都是有向边,则称该图为有向图(directed graphs)。
如下面的有向图G = (V, {E}) 来说,顶点集 V = {1,2,3},边集合E = {<1,2>,<2,1>,<2,3>}。
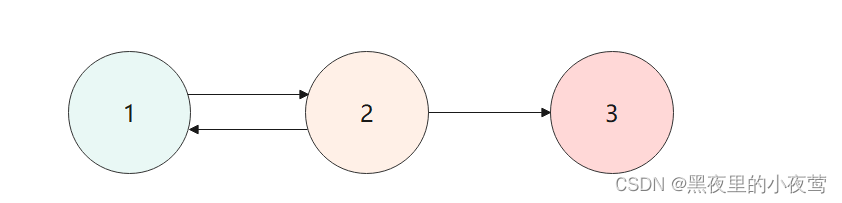
注:上图中连接1到2的有向边就是弧,1是弧尾,2是弧头,<1,2>表示弧,不像无向边,表示有向边的顶点顺序不能无序,即<1,2>表示的弧,不能写成<2,1>。
对于有向图 G = (V, {E}),如果弧<V,V
>
E,则称顶点 V
邻接到顶点 V
。
以顶点 v 为头的弧的数目称为v的入度(InDegree),记为 ID(v);以v为尾的弧的数目称为v的出度(OutDegree),记为OD(v);顶点v的度为TD(v) = ID(v) + OD(v),即顶点v的度等于v的出度与入度之和。
上面有向图中,顶点2的出度为 2、入度为 1、度为 3,其它顶点依次类推。
对于具有n个顶点、e条边的有向图,ID(V
) =
OD(V
) = e,即有向图的全部顶点的入度之和与出度之和相等,并且等于边数,这是因为每条有向边都有一个起点和终点。
无向边用小括号"()"表示,而有向边则是用尖括号"<>"表示。
二、图的种类
(1)简单图、多重图
一个图G满足:不存在重复的边;②不存在顶点到自身的边,则称图G为简单图。上面的无向图和有向图都是简单图。
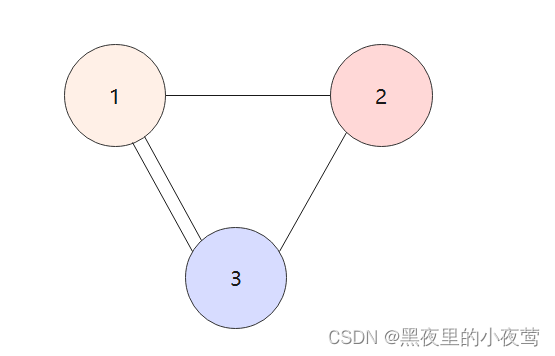
如果图G中某两个顶点之间的边数大于1条,允许顶点通过一条边和自身关联,则称图G为多重图。下图都不是简单图,而是多重图。
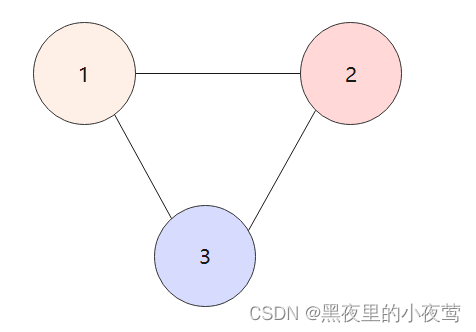
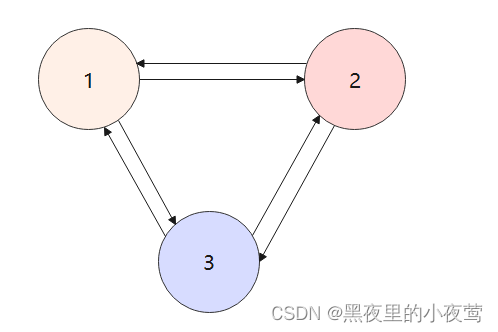
(2)完全图(也称简单完全图)
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有 n(n-1)/2 条边。
在有向图中,如果任意两个顶点之间都存在方向相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有 n(n-1) 条边。
如下图,有一个无向完全图和一个有向完全图。
总结:对于具有n个顶点和e条边数的图,无向图 0
e
n(n-1)/2,有向图 0
e
n(n-1)。
(3)稠密图、稀疏图
边数很少的图称为稀疏图,反之称为稠密图。稀疏和稠密本身是模糊的概念,稀疏图和稠密图常常是相对而言的。一般当图G满足 |E| < |V|log|V|时,可以将G视为稀疏图。
(4)子图
设有两个图 G1 = (V1, E1) 和 G2 = (V2, G2),若 V2 是 V1 的子集,且 E2 是 E1的子集,则称G2是G1的子图。若有满足V1(G1) = V2(G2) (即子图G2的顶点和图G1的顶点数相同)的子图G2,则称其为G1的生成子图。如下图中G2是G1的子图:
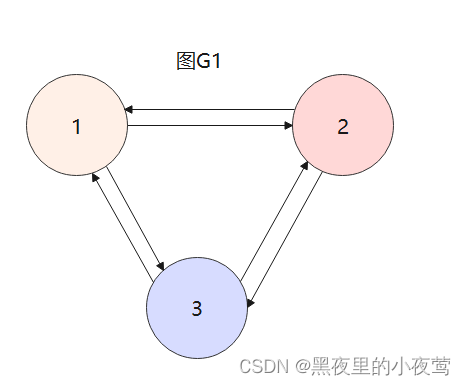
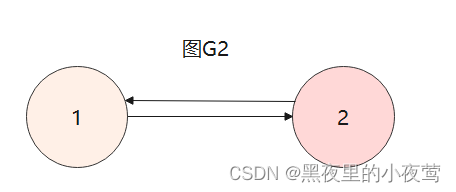
注:并非V和E的任何子集都能构成G的子图,因为这样的子集可能不是图,即E的子集中的某些边关联的顶点可能不在这个V的子集中。
(5)连通、连通图和连通分量
在无向图G中,如果从顶点 v 到顶点 w 有路径存在,则称 v 和 w 是连通的。如果图G中任意两个顶点 V 、V
V,V
和 V
都是连通的(即任意两个顶点连通),则称G是连通图(Connected Graph)。
无向图中的极大连通子图称为连通分量。注意连通分量的概念,它强调:
- 要是子图;
- 子图要是连通的;
- 连通子图含有极大顶点数;
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边。
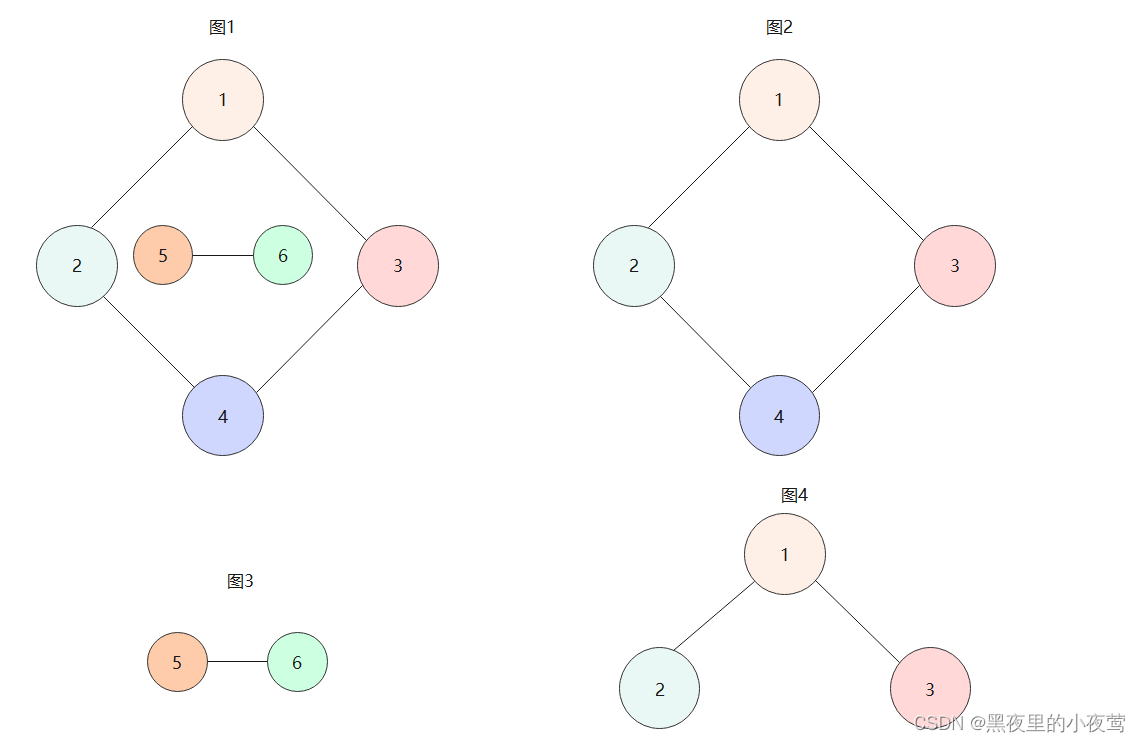
上图的图1是一个无向非连通图。但是它有两个连通分量,即图2和图3.而图4尽管是图1的子图,但它却不满足连通子图的极大顶点数。因此它不是图1的无向图的连通分量。
如果一个图有 n 个顶点,如果边数小于 n - 1,那么此图必是非连通图。如果图是非连通图,那么最多可以有多少条边?
非连通情况下边最多的情况:由 n-1 个顶点构成一个完全图,此时再任意加入一条边则变成连通图。
例题:
若无向图 G = (V, E) 中含有7个顶点,要保证图G在任何情况下都是连通的,则需要的边数最少是()。
A、6 B、15 C、16 D、21
答案及解析:C
先将 n-1 = 6 个顶点构成一个完全图,需要 6(6-1)/2 = 15 条边,此时再加入一条边于剩下的那个顶点连接必定构成连通图。
(6)强连通图、强连通分量
在有向图中,如果有一对顶点 v 和 w,从 v 到 w 和 w 到 v 之间都有路径,则称这两个顶点是强连通的。如果图中任何一对顶点都是强连通的,则称此图为强连通图。
有向图中的极大强连通子图(最大强连通子图)称为有向图的强连通分量。如下图:
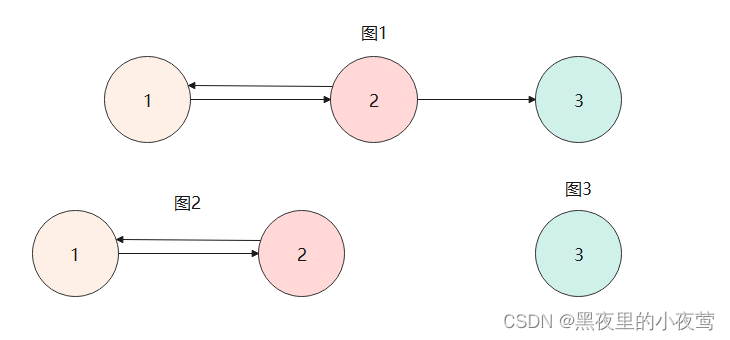
图1不是强连通图,因为顶点 3 到 顶点 1 不存在路径,而 顶点 1 到 顶点 3 存在路径。。图2和图3是强连通图,它们是图1的强连通分量。
如果一个有向图有 n 个顶点,如果是强连通图,那么最少需要多少条边?
有向图强连通情况下边最少的情况:至少需要 n 条边,构成一条环路。
注:在无向图中讨论连通性,在有向图中讨论强连通性。
三、图中的一些术语
(1)生成树、生成森林
连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为 n,则它的生成树含有 n -1 条边。包含图中全部顶点的极小连通子图,只有生成树满足这个极小条件,对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。在非连通图中,连通分量的生成树构成了非连通图的森林。如下图:
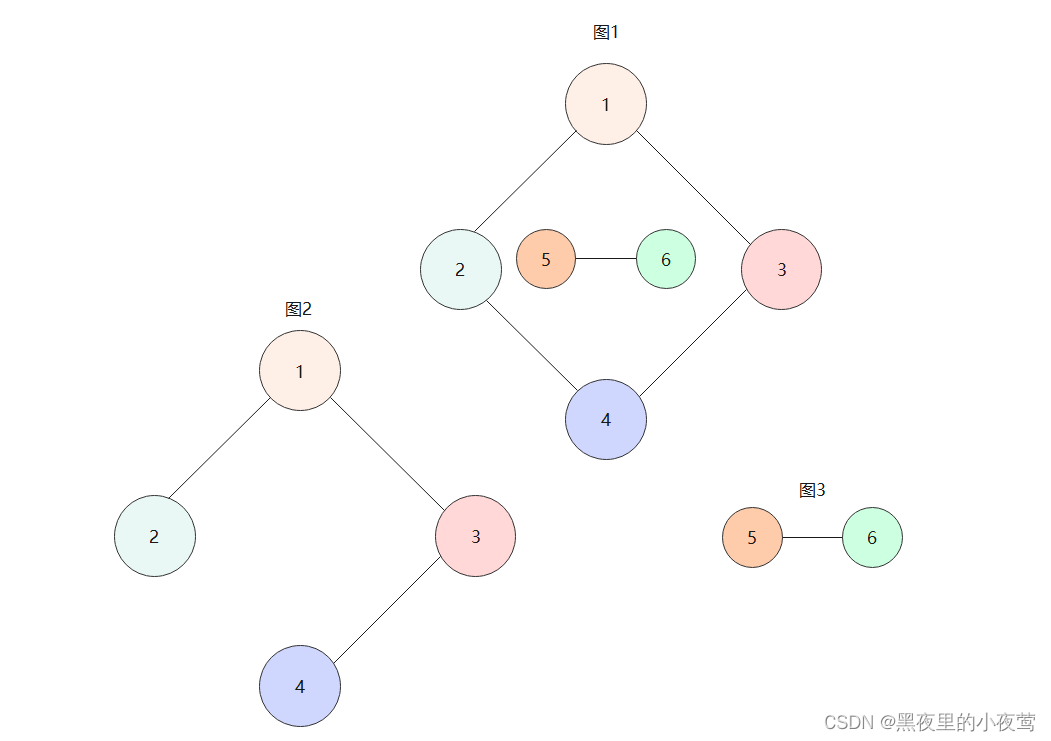
图1是非连通图,故由其连通分量来生成树,图2和图3是图1的连通分量的生成树,且图2和图3构成森林。
注:区分极大连通子图和极小连通子图。极大连通子图是无向图的连通分量,极大即要求该连通子图包含其所有的边;极小连通子图是既要保持图的连通性又要使得边数最少的子图。
(2)边的权和网
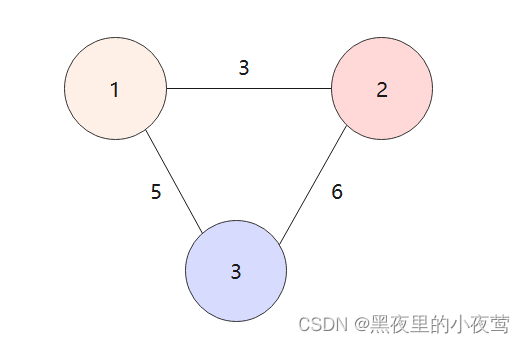
在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权(Weight)。这种边上带有权值的图称为带权图,也称网(Network)。如下图就是一张带权图:
(3)路径、路径长度和回路
顶点 V 到顶点 V
之间的一条路径是指顶点序列 V
,V
,V
,...,V
,V
。路径上边的数目称为路径长度。第一个顶点和最后一个顶点相同的路径称为回路或环。
若一个图有n个顶点,并且有大于 n-1 条边,则此图一定有环。
(4)简单路径、简单回路
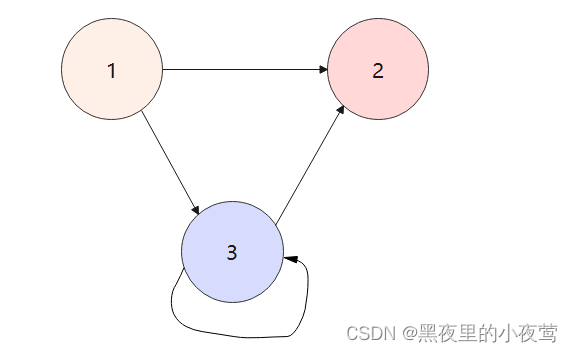
在路径序列中,顶点不重复出现的路径称为简单路径。除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。如下图:
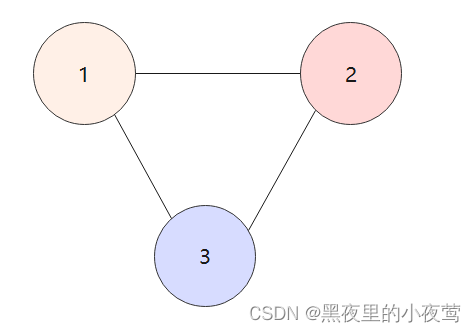
路径 1 -> 2 -> 3是一条简单路径,其长度为 2,路径 1-> 2 -> 3 -> 1是一个简单回路,其长度为3。
(5)距离
从顶点 u 出发到顶点 v 的最短路径若存在,则此路径的长度称为从 u 到 v 的距离。若从 u 到 v 根本不存在路径,则记该距离无穷(∞)。
(6)有向树
一个顶点入度为 0、其余顶点的入度均为 1 的有向图,则称为有向树。(其中入度为0其实相当于树的根结点,其余顶点入度为1就是说树的非根结点的双亲只有一个)。
一个有向图的生成森林由若干棵有向树组成,含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧。如下图:
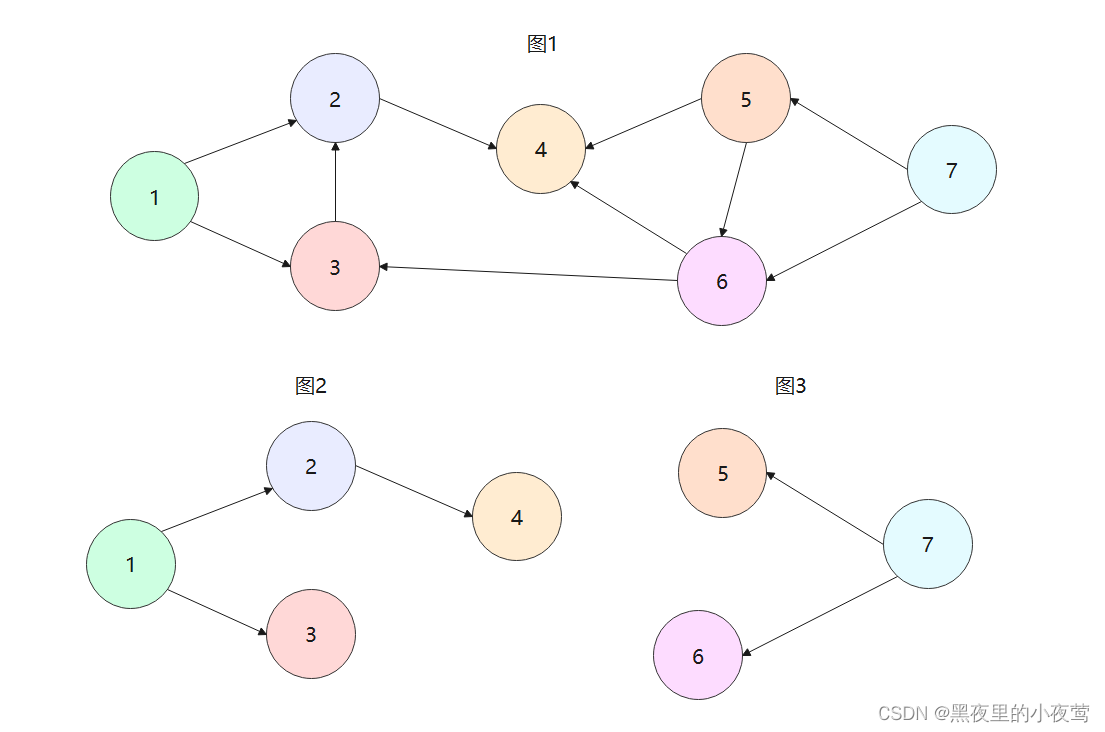
上图中,图1是有向图。去掉一些弧后,它可以分解为两颗有向树,如图2和图3,这两颗就是图1有向图的生成森林。
环境不会改变,解决之道在于改变自己,看这篇文章的每一个人,在这里为你们加油。






















 8336
8336











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








