DV-Hop算法1——最基础算法的介绍

#DV-Hop算法实现
原始 DV-Hop 算法在 2003 年被 Dragos Niculescu 率先提出，其核心思想主要包括如下三步：
##步骤1：节点间最小跳数的计算
各信标节点以泛洪的方式向网络中广播数据包，主要包括信标节点的位置坐标和初始化为0的跳数值。当相邻的节点收到后，仅保存来自同一信标的最小跳数值作为到该信标节点的最小跳数，并将数值加1后继续传递给相邻节点。泛洪结束后，所有节点都能够知道各信标节点的最小跳数。
##步骤2：节点间距离的估算
信标节点采取无偏估计的方式计算平均跳距，如下公式

上式中，$AH{S}_i$代表信标节点i的平均跳距，$N_a$为信标节点的个数，（$x_i$,$y_i$）和（$x_j$,$y_j$）分别代表信标节点i和j的位置坐标，$h_{ij}$代表信标节点i和j之间的最小跳数。
信标节点的平均跳距向网络中广播后，未知节点取率先收到的信标节点的平均跳距作为自己的平均跳距，可根据以下公式求得未知节点与信标节点的估计距离。
$$d_{ui}=AH{S}_u\ast h_{ui}$$
上式中，$AH{S}_u$代表未知节点u的平均跳距，$h_{ui}$和$d_{ui}$分别为信标节点i到未知节点u的最小跳数和估计距离。
##步骤3：未知节点坐标的求取
在对距离进行估算之后，结合信标节点的已知信息，得出以下距离方程组：

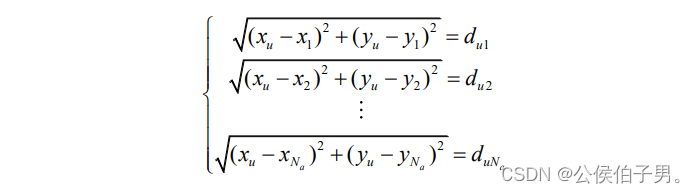
将前$N_a$-1个方程依次减去最后一个方程，可以得到线性化的方程组：

用最小二乘法求解上式可以得出未知节点的坐标：
$$X=(A^{T}A{)}^{-1}{A}^{T}B$$

以上三个步骤实现DV-Hop算法对节点的定位。