第二章 整数规划 习题 2（司守奎数模第三版）

一、非线性的0-1规划问题转换成线性的0-1规划问题

将非线性的0-1规划问题转换为线性的0-1规划问题

涉及非线性转换，参考文章非线性如何线性化？

如图，可以知道需要将x₁x₂转换为y，即y=x₁x₂，得到以下关系

从而得到如下的线性0-1规划：

二、选择最优校址问题

解：令

（1）小区A₁可以备选校址B₁、B₂、B₃处所建立的学校覆盖，则有约束条件
x₁+x₂+x₃≥1.
（2）小区A₂可以备选校址B₂、B₄处所建立的学校覆盖，则有约束条件
x₂+x₄≥1.
（3）小区A₃可以备选校址B₃、B₅处所建立的学校覆盖，则有约束条件
x₃+x₅≥1.
以此类推，建立如下的0-1整数规划模型：

求得在备选校址B₁、B₄、B₅处建小学。
基于问题求解的Matlab程序如下：

clc,clear
x=optimvar('x',6,'Type','integer','LowerBound',0,'UpperBound',1)
prob=optimproblem;prob.Objective=sum(x);
cons=[x(1)+x(2)+x(3)>=1;x(2)+x(4)>=1;x(3)+x(5)>=1
    x(4)+x(6)>=1;x(5)+x(6)>=1;x(1)>=1
    x(2)+x(4)+x(6)>=1];
prob.Constraints.cons=cons;
[sol,fval,flag]=solve(prob),sol.x

三、某企业分配设备使获得最大利润问题

用j=1，2，3，4分别表示甲、乙、丙、丁4个企业，c_ij表示第i（i=1，2，…，6）台设备分配给第j个企业创造的利润，引进0-1变量

则问题的数学模型为：

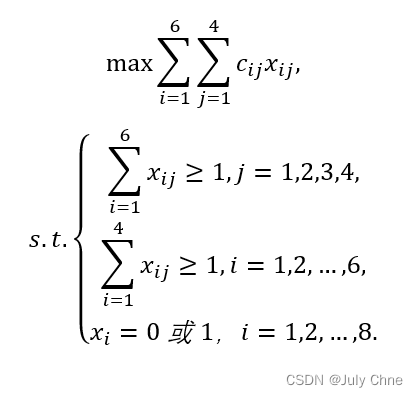
求得x₁₄=x₂₁=x₃₃=x₄₂=x₅₂=x₆₂=1，其他x_ij=0.最大利润为44。

clc,clear,c=[4,2,3,4;
             6,4,5,5;
             7,6,7,6;
             7,8,8,6;
             7,9,8,6;
             7,10,8,6;];
x=optimvar('x',6,4,'Type','integer','LowerBound',0,'UpperBound',1)
prob=optimproblem('ObjectiveSense','max')
prob.Objective=sum(sum(c.*x));
prob.Constraints.cons1=sum(x,1)>=1;
prob.Constraints.cons2=sum(x,2)==1
[sol,fval,flag]=solve(prob),sol.x