【数学建模】第一章线性规划

July Chne

已于 2023-07-16 18:28:04 修改

阅读量258

点赞数

文章标签：数学建模

于 2023-07-13 19:50:13 首次发布

本文链接：https://blog.csdn.net/qq_62614888/article/details/131707783

版权

本文为司守奎老师的《数学建模算法与应用》第三版内容。

1.1 线性规划问题

在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支——数学规划,而线性规划( LinearProgramming,LP)则是数学规划的一个重要分支。自从1947年G.B. Dantzig 提出求解线性规划的单纯形方法以来,线性规划在理论上趋向成熟,在实用中日益广泛与深入。特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后,线性规划的适用领域更为广泛了,已成为现代管理中经常采用的基本方法之一。

1.1.1 线性规划的实例与定义

例1.1
例1.1 图
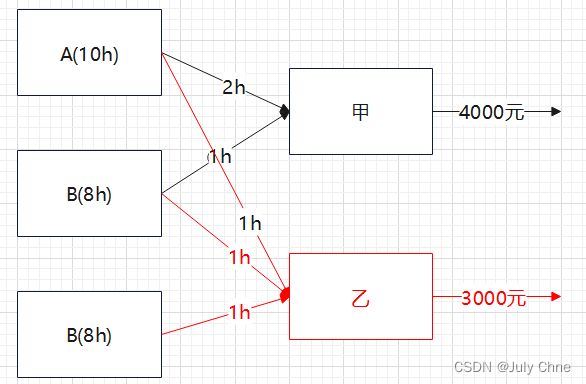
根据上述问题的数学模型：设该厂生产x₁台甲机床和x₂乙机床时总利润z最大，则x₁，x₂应满足
例1.1
式中：变量x₁，x₂为决策变量。式（1.1）称为问题的目标函数，式（1.2）中的几个不等式是问题的约束条件，记为s.t.（即subject to）。由于上面的目标函数及约束条件均为线性函数，故称为线性规划问题。

*/ 1.1.2 线性规划问题的解的概念
一般线性规划问题的（数学）标准型为
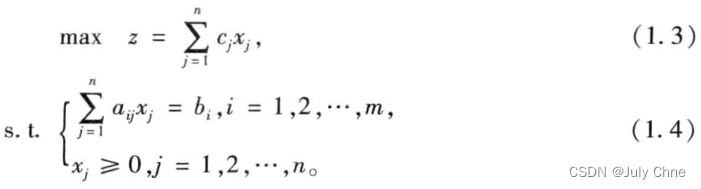
在这里插入图片描述
式中：b_i≥0，i=1，2，…，m。
可行解 满足约束条件式（1，4）的解x=[x₁，…x_n]^T，称为线性规划问题的可行解，而使目标函数式（1，3）达到最大值的可行解称为最优解。
可行域 所有可行解构成的集合称为问题的可行域，记为R。
灵敏度分析 对于数学建模，一定需要进行灵敏度分析。在这里不详讲。

1.1.3 线性规划的Matlab标准形式及软件求解

线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于等号也可以是大于等号。为了避免这种形式多样性带来的不便, Matlab中规定线性规划的标准形式为
在这里插入图片描述
式中：f，x，b，beq，lb，ub为列向量，其中f称为价值向量，b称为资源向量；A，Aeq为矩阵。
Matlab中求解线性规划的命令为

[x,fval]=linprog(f,A,b)
[x,fval]=linprog(f,A,b,Aeq,Beq)
[x,fval]=linprog(f,A,b,Aeq,Beq,lb,ub)

式中：x返回决策向量的取值；fval返回目标函数的最优值；f为价值向量；A和 b对应线性不等式约束；Aeq 和 beq对应线性等式约束；lb和 ub分别对应决策向量的下界向量和上界向量。
在这里插入图片描述
解利用Matllab程序，求得最优解为：x₁=2，x₂=6，目标函数的最优值z=26。
基于求解器求解的Matlab程序如下：

clc,clear
c=[4;3];b=[10;8;7];
a=[2,1;1,1;0,1];lb=zeros(2,1);
[x,fval]=linprog(-c,a,b,[],[],lb)	%没有等号约束
y=-fval		%目标函数为最大化

运行结果

Optimal solution found.
x =
    2.0000
    6.0000
fval =
   -26
y =
    26

基于问题求解的Matlab程序如下：

clc,clear
prob=optimproblem('ObjectiveSense','max')	%目标函数最大化的优化问题
c=[4;3];b=[10;8;7];
a=[2,1;1,1;0,1];
x=optimvar('x',2,'LowerBound',0);	%决策变量
prob.Objective=c'*x;	%目标函数
prob.Constraints.con=a*x<=b;	%约束条件
[sol,fval,flag,out]=solve(prob)	%fval返回最优值
sol.x	%显示决策变量的值

运行结果

prob = 
  OptimizationProblem - 属性:
       Description: ''
    ObjectiveSense: 'maximize'
         Variables: [0×0 struct] containing 0 OptimizationVariables
         Objective: [0×0 OptimizationExpression]
       Constraints: [0×0 struct] containing 0 OptimizationConstraints
  No problem defined.
Solving problem using linprog.
Optimal solution found.
sol = 
  包含以下字段的 struct:
    x: [2×1 double]
fval =
    26
flag = 
    OptimalSolution
out = 
  包含以下字段的 struct:
         iterations: 3
    constrviolation: 0
            message: 'Optimal solution found.'
          algorithm: 'dual-simplex'
      firstorderopt: 8.8818e-16
             solver: 'linprog'
ans =
    2.0000
    6.0000

例1.3 求解下列线性规划问题：
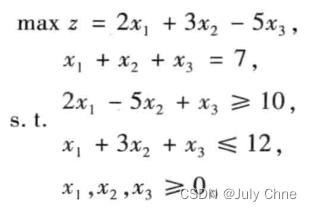
在这里插入图片描述
解：

f=[-2;-3;5];
a=[-2,5,-1;1,3,1];b=[-10;12];
aeq=[1,1,1];beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1))
y=-y

运行结果

Optimal solution found.
x =
    6.4286
    0.5714
         0
y =
  -14.5714
y =
   14.5714

习题 1

1.1 求解下列线性规划问题

在这里插入图片描述
解：

clc;
c=[-1,1,1];
a=[1,-2,1;4,-1,-2];b=[11,-3];
aeq=[-2,0,1];beq=1;
[x,y]=linprog(c,a,b,aeq,beq,zeros(3,1),[])

运行结果

Optimal solution found.
x =
         0
    1.0000
    1.0000
y =
    2.0000

1.2

在这里插入图片描述
解：

% 例题2
clear;clc
% 由于有绝对值的问题,所以需要将变量进行代换
c=[1:4,1:4]';
%令ui=(xi+|xi|)/2,vi=(|xi|-xi)/2
Aeq=[1,-1,-1,1;
    1,-1,1,-3;
    1,-1,-2,3];
Aeq=[Aeq,-Aeq]
beq=[0,1,-0.5];
[y,z]=linprog(c,[],[],Aeq,beq,zeros(8,1));
x=y(1:4)-y(5:end)
z

运行结果

1.3

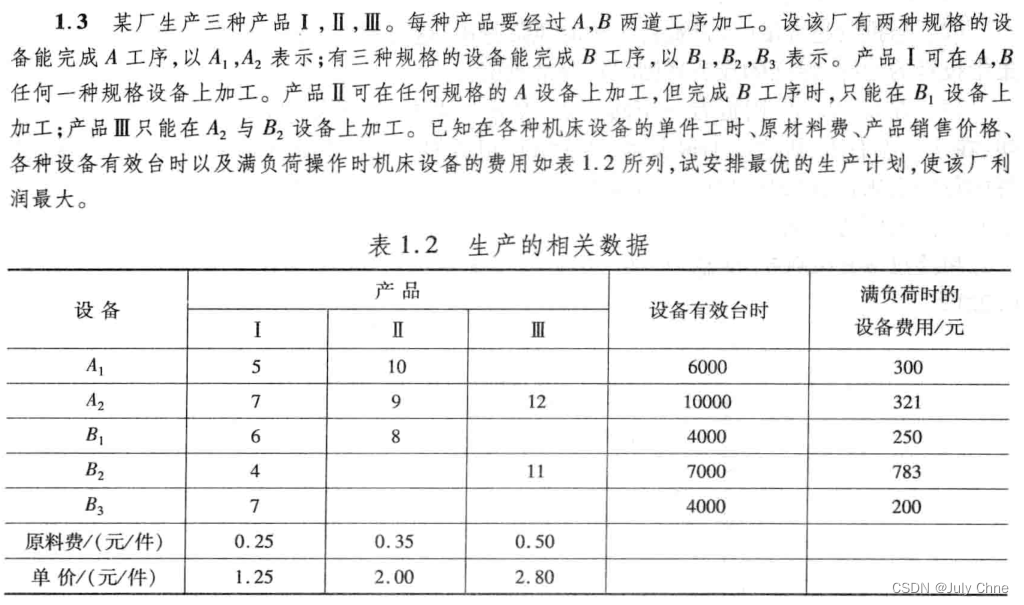
在这里插入图片描述
解：对产品Ⅰ来说，设以A₁、A₂完成A工序的产品分别为x₁、x₂件，转入B工序时，以B₁、B₂、B₃完成B工序的产品分别为x₃、x₄、x₅件；对产品Ⅱ来说，设以A₁、A₂完成A工序的产品分别为x₆、x₇件，转入B工序时，以B₁完成B工序的产品分别为x₃、x₈件；对产品Ⅲ来说，设以A₂完成A工序的产品分别为x₉、件，转入B工序时，以B₂完成B工序的产品分别为x₉件.由上述条件可得

x₁+x₂=x₃+x₄+x₅，x₆+x₇=x₈
由题目所给的数据可建立如下的线性规划模型：
这里是我参考答案得到的，个人理解这里的-300/6000、-321/10000等等是修好设备需要那么多钱，即为分子，然后修好之后可以使用这么多时长，即为分母。
max z=（）

这里我们得到max z
z = (1.25-0.25)(x1+x2)+(2 -0.35)x8+(2.8-0.5)x9
- (300/6000)(5x1+10x6) - (321/10000)(7x2+9x7+12x9) 
- (250/4000)(6x3+8x8) - (783/7000)(4x4+11x10) - (200/4000)7x5
显然，我们需要将z进行化简再放入matlab运算
z=3/4 x1 + 452/583 x2 - 3/8 x3 - 783/1750   x4 - 7/2x5
 - 1/2 x6 - 583/2018  x7 + 23/20 x8 + 670/979 x9

此处和之前不同，需要引入整数规划
一、整数规划的分类
（1）线性整数规划：可以直接使用matlab求解
（2）非线性整数规划：无特定算法，只能够用近似算法，如蒙特卡洛模拟，智能算法。
（3）0-1规划：特殊的整数规划，matlab中只能做到线性0-1规划，非线性0-1规划只能做近似求解。

二、线性规划与整数线性规划
线性规划：[x,fval]=linprog[c,A,b,Aeq,beq,lb,ub,x0]
非线性规划：[x,fval]=intlinprog[c,intcon,A,b,Aeq,beq,lb,ub]

可见：1.整数线性规划中缺少了x0，不能指定初始值。
2.增加了intcon。intcon表示指定第某个变量是整数变量。
如：
intcon=3；表示第三个变量是整数变量。
intcon=[1,3];表示第一个和第三个是整数变量。
intcon=[1:9];表示第一个到第九个都是整数变量。
其他用法与线性规划相同。

针对0-1规划，通常是在ub与lb上做文章，使得只能够取得0或者1。
此处参考文章整数规划matlab实现与实例

clc;clear;format short
c = [3/4,452/583,-3/8,-783/1750,-7/20,-1/2,-583/2018,23/20,670/979];
A = [5,zeros(1,4),10,zeros(1,3);
    0,7,zeros(1,4),9,0,12;
     0,0,6,zeros(1,4),8,0;
     zeros(1,3),4,zeros(1,4),11;
     zeros(1,4),7,zeros(1,4)];
b = [6000,10000,4000,7000,4000];
aeq = [1,1,-1,-1,-1,zeros(1,4);
       zeros(1,5),1,1,-1,0;];
beq = [0;0];
%整数规划
intcon = [1:9];
[x,y]= intlinprog(-c,intcon,A,b,aeq,beq,zeros(9,1));
x,y=-y

运行结果

x =
   1.0e+03 *	%这里的意思是以科学计数法显示，即为1.0*10^3，也就是将后面的所有数字乘1000
    1.2000
    0.2300
         0
    0.8590
    0.5710
         0
    0.5000
    0.5000
    0.3240
y = 1.1464e+03	%同x

1.4

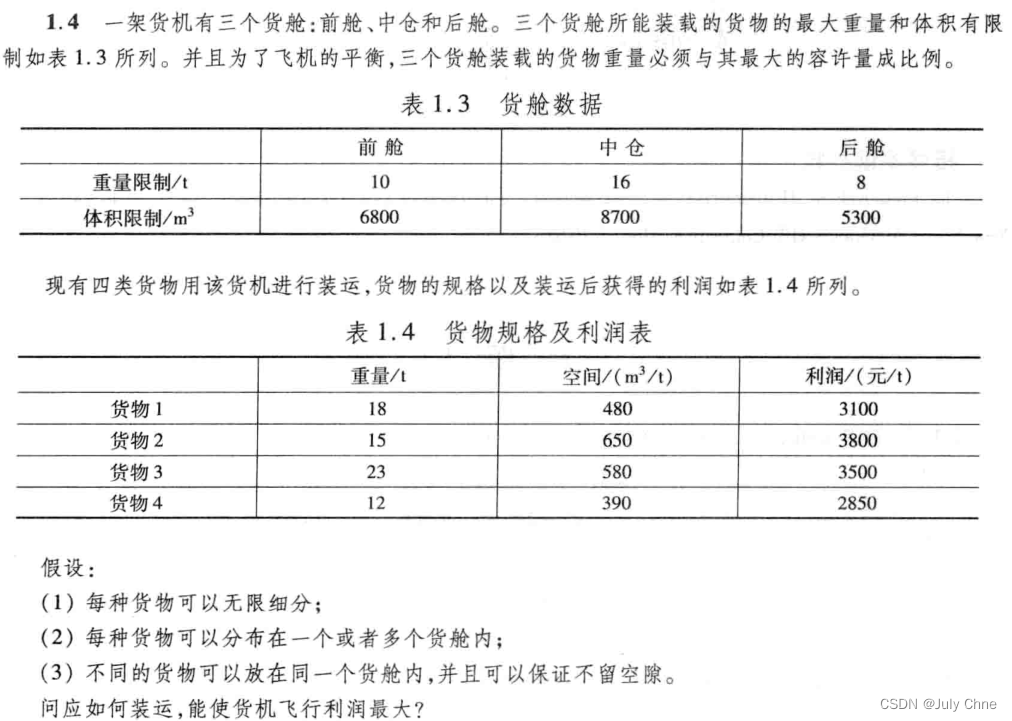
在这里插入图片描述
解：
用i=1，2，3，4分别表示货物1、货物2、货物3、货物4；j=1，2，3分别表示前舱、中仓、后舱；设x_ij（i=1,2,3,4；j=1,2,3）分别表示第i种货物放在第j个货舱内的重量，w_j，v_j（j=1,2,3）分别表示第j个舱的重量限制和体积限制，a_i，b_i，c_i（i=1,2,3,4）分别表示可以运输的第i种货物的质量，单位质量所占的空间和单位货物的利润。
（1）目标函数

（2）约束条件
四种货物的重量约束

三个货舱的重量限制

三个货舱的体积限制请添加图片描述
三个货舱装入货物的平衡限制

综上所述，再加决策变量的非负性约束，建立如下线性规划模型：

July Chne

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【数学建模】第一章线性规划

根据上述问题的数学模型：设该厂生产x1台甲机床和x2乙机床时总利润z最大，则x1，x2应满足式中：变量x1，x2为决策变量。式（1.1）称为问题的目标函数，式（1.2）中的几个不等式是问题的约束条件，记为s.t.（即subject to）。由于上面的目标函数及约束条件均为线性函数，故称为线性规划问题。*/ 1.1.2 线性规划问题的解的概念一般线性规划问题的（数学）标准型为式中：bi可行解满足约束条件式（1，4）的解x=[x1，…xnT。
复制链接

扫一扫