普朗克单色辐出度与功率体密度关系简单证明

Herna.

已于 2024-06-28 16:57:46 修改

阅读量302

点赞数 10

文章标签：笔记其他

于 2024-06-28 16:28:51 首次发布

本文链接：https://blog.csdn.net/qq_62711060/article/details/140029050

版权

普朗克辐射理论

基于普朗克对黑体辐射的讨论，得到的结果一般有如下形式：

$\rho_{\nu} =\dfrac{8\pi \rm h\nu^3}{\rm c^3} \cdot \dfrac{1}{\rm e^{\frac{\rm h\nu}{kT}}-1}$

$M(\nu,T)=\dfrac{2\pi \rm h \nu^3}{\rm c^2} \cdot \dfrac{1}{\rm e^{\frac{\rm h \nu}{k T}}-1}$

第一式为功率体密度，即：

$\rho_{\nu}=\dfrac{\rm d E}{\rm dV \rm d \nu}$

上式中 $E$ 为能量， $V$ 为体积， $\nu$ 为频率。

第二式是单色能量辐出度：

$M(\nu, T) = \dfrac{\rm d E}{\rm d \nu \rm d S}$

那么一式和二式有什么联系呢？

$\rho_{\nu}=\dfrac{4}{\rm c}\cdot M(\nu, T)$

下面对此结论进行证明。

二者联系证明

如图光源从元面积为 $\rm ds$ 的小孔发射光束，该光束是在一立体角 $\varOmega$ 范围发散的点光源，该点光源在空间某一平面上的面积如图，则可以微元法根据球坐标系的 $\theta$ 求出元面积对应的立体角元 $\rm d \varOmega$ 。

$\rm d \varOmega = \dfrac{\rm d S}{r^2} = \dfrac{2\pi \sin\theta r \rm d \theta}{r^2}$

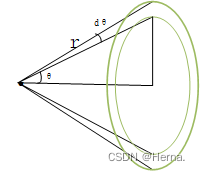
这是一个空间量，光源从小孔出射产生能量，左边的光源在元面积 $\rm d s$ 上产生的能量为 $c\rm d s\rho_{\nu} \rm d t$ ,该能量也是小孔在单位球体积元内辐射的能量，所以右边一个立体角内的能量是 $c\rm d s \rho_{\nu} \rm dt \dfrac{\rm d \varOmega}{4\pi}$ 其中 $4\pi$ 是空间球面总的立体角。

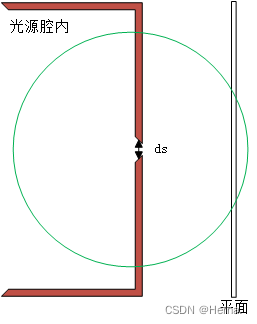
则有发散到右边的平面上的总能量通量为：

$\varPhi = \dfrac{E}{\rm d t}=\displaystyle{\int {c\rm ds \rho_{\nu}\dfrac{\rm d \varOmega}{4 \pi}\cos\theta}}$

这是在球坐标系，其中 $\cos\theta$ 为立体角元对应面积在平面上的投影，则：

$\begin{aligned} M(\nu,T)&=\dfrac{\varPhi}{\rm ds} =\displaystyle{\int {c\rho_{\nu}\dfrac{\rm d \varOmega}{4 \pi}\cos\theta}}=\dfrac{c\rho_{\nu}}{4\pi}\cdot\displaystyle{\int^{\frac{\pi}{2}}_{0}2\pi\sin\theta\cos\theta\rm d \theta}\\ &=\dfrac{c\rho_{\nu}}{4\pi}\cdot\dfrac{\pi}{2}\cdot\displaystyle{\int^{\pi}_{0}sin\varphi\rm d \varphi} = \dfrac{c}{4}\cdot\rho_{\nu} \end{aligned}$