地球重力场模型计算各种重力场参量

一、计算说明

1.1规格化缔合勒让德函数

前面博客已发

1.2坐标转换

1.3重力场的参数的球谐级数表示 

1.3.1球谐系数

1.3.2 扰动位

1.3.3 大地水准面高

1.3.4 重力异常

1.3.5 重力扰动

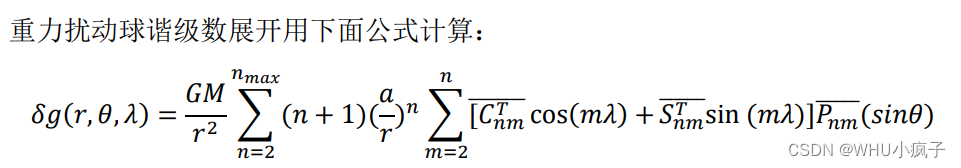
 二 关键

1.二维vector容器使用。

2.类设计

3.高阶次计算，提升计算效率问题

三 代码

3.1函数声明文件

#pragma once
#include<iostream>
#include<fstream>
#include<string>
#include<vector>
#include<iomanip>
using namespace std;
const double PI = 3.14159265358979323;
const double GM = 3986005e8;
const double a = 6378137;
const double f = 1.0 / 298.257223563;
const double w = 7.292115e-5;
class Zone
{
public:
	double B;//大地纬度
	double L;//大地经度
	double H;//大地高
	double r;
	double theta;
	double lambda;//球坐标
	double T=0.0;//扰动位
	double N=0.0;//大地水准面高
	double dg1=0.0;//重力异常
	double dg2=0.0;//重力扰动
	double gamma;//正常重力
	vector<vector<double>> P;//完全规格化缔合朗让德系数
	void BLH_to_rthetalamda();//大地坐标转化球坐标
	void calculate_Pnm();//计算完全规格化缔合朗让德系数P
	void calculate_gamma();//计算正常重力
	void calculate(vector<vector<double>> *Ct, vector<vector<double>> *St);//计算扰动位
};
double degree_to_radian(double degree);//角度转换为弧度

void read_Cnm_Snm(vector<vector<double>> * C, vector<vector<double>> * S);//读取SGG-UGM-1.gfc中的数据到C,S

void calculate_Ct_St(vector<vector<double>> *C, vector<vector<double>> *S, vector<vector<double>> *Ct, vector<vector<double>> *St);//计算扰动位规格化系数Ct,St

 3.2函数定义文件

#include"wxf.h"
double degree_to_radian(double degree)//角度转换为弧度
{
	double rad = degree / 180.0 * PI;
	return rad;
}
void read_Cnm_Snm(vector<vector<double>>* C, vector<vector<double>>* S)//读取SGG-UGM-1.gfc中的数据
{
	ifstream infile;
	string aline;
	int m, n;
	infile.open("SGG-UGM-1.gfc");
	for (int i = 0; i < 39; i++) getline(infile, aline);
	for (int i = 0; i < 65341; i++)
	{
		getline(infile, aline);
		n = atoi(aline.substr(5, 3).c_str());
		m = atoi(aline.substr(10, 3).c_str());
		(* C)[n][m] = atof(aline.substr(16, 21).c_str());
		(* S)[n][m] = atof(aline.substr(40, 21).c_str());
	}
	infile.close();
}
void calculate_Ct_St(vector<vector<double>> *C, vector<vector<double>> *S, vector<vector<double>> *Ct, vector<vector<double>> *St)//计算扰动位规格化系数Ct,St
{
	for (int i = 0; i < 361; i++)
	{
		for (int j = 0; j < i + 1; j++)
		{
			(*Ct)[i][j] = (*C)[i][j];
			(*St)[i][j] = (*S)[i][j];
		}
	}
	double J2 = 108263e-8;
	double J4 = -2.37091222e-6;
	double J6 = 6.08347e-9;
	double J8 = -1.427e-11;
	(*Ct)[2][0] = (*Ct)[2][0] + J2 / sqrt(5);
	(*Ct)[4][0] = (*Ct)[4][0] + J4 / 3.0;
	(*Ct)[6][0] = (*Ct)[6][0] + J6 / sqrt(13);
	(*Ct)[8][0] = (*Ct)[8][0] + J8 / sqrt(17);
}
void Zone::BLH_to_rthetalamda()//大地坐标转化球坐标
{
	double BB = degree_to_radian(B);
	double LL = degree_to_radian(L);
	double b = a - a * f;
	double e2 = (a * a - b * b) / a / a;
	double N = a / sqrt(1 - e2 * sin(BB) * sin(BB));
	double X = (N + H) * cos(BB) * cos(LL);
	double Y = (N + H) * cos(BB) * sin(LL);
	double Z = (N * (1 - e2) + H) * sin(BB);
	r = sqrt(X * X + Y * Y + Z * Z);
	theta = atan2(sqrt(X * X + Y * Y), Z);
	lambda = atan2(Y, X);
	if (lambda < 0) lambda = lambda + 2 * PI;
}
void Zone::calculate_Pnm()//完全规格化缔合朗让德系数
{
	P.resize(361, vector<double>(361));
	//种子点
	P[0][0] = 1;
	P[1][0] = sqrt(3) * cos(theta);
	P[1][1] = sqrt(3) * sin(theta);
	for (int l = 2; l < 361; l++)
	{
		double f1 = sqrt(1 + 1.0 / 2 / l);
		double f2 = sqrt(2 * l + 1);//f1,f2与m无关，只与每一行的后两项递推有关
		for (int m = 0; m < l - 1; m++)//每一行除了后两个的递推循坏，因为需要前面两行的值，这两列前面不够两个
		{
			double f3 = sqrt((2.0 * l + 1.0) / (l - m) / (l + m));
			double f4 = sqrt(2.0 * l - 1.0);
			double f5 = sqrt((l - m - 1) * (l + m - 1) * 1.0 / (2.0 * l - 3.0));//f3,f4,f5
			P[l][m] = f3 * (f4 * cos(theta) * P[l - 1][m] - f5 * P[l - 2][m]);
		}
		P[l][l - 1] = f2 * cos(theta) * P[l - 1][l - 1];//每一行倒数第二个的递推，用到这一列上一个的值
		P[l][l] = f1 * sin(theta) * P[l - 1][l - 1];//每一行倒数第一个的递推，因为他是这一列的起点，递推用到前一行前一列的值
	}
}
void Zone::calculate_gamma()//计算正常重力
{
	double x = degree_to_radian(B);
	//中间量的定义与计算
	long double b = a - a * f;
	long double m = w * w * pow(a,2) * b / GM;
	long double E = sqrt(a * a - b * b);
	long double e2 = E / b;
	long double q0 = 1.0 / 2 * ((1 + 3 * b * b / E / E) * atan2(E, b) - 3 * b / E);
	long double dq0 = 3 * (1 + b * b / E / E) * (1 - b / E * atan2(E, b)) - 1;
	//计算赤道上正常重力
	long double ra = GM / a / b * (1 - m - m * e2 * dq0 / 6.0 / q0);
	//计算两极上正常重力
	long double rb = GM / a / a * (1 + m * e2 * dq0 / 3.0 / q0);
	//计算椭球面上的正常重力
	long double r = (a * ra * cos(x) * cos(x) + b * rb * sin(x) * sin(x)) / sqrt(a * a * cos(x) * cos(x) + b * b * sin(x) * sin(x));
	//计算椭球以上的正常重力值
	gamma = r * (1 - 2 * (1 + f + m - 2 * f * sin(x) * sin(x)) * H / a + 3 * H * H / a / a);
}
void Zone::calculate(vector<vector<double>> *Ct, vector<vector<double>> *St)//计算扰动位
{
	for (int n = 2; n < 361; n++)
	{
		for (int m = 0; m < n + 1; m++)
		{
			double co = cos(m * lambda), si = sin(m * lambda);
			T  += GM / r * pow(a / r, n) * ((*Ct)[n][m] * co + (*St)[n][m] * si) * P[n][m];//计算扰动位
    		dg1 += GM / r/r * (n - 1) * pow(a / r, n) * ((*Ct)[n][m] * co + (*St)[n][m] * si) * P[n][m];//计算重力异常
            dg2 += GM / r /r* (n + 1) * pow(a / r, n) * ((*Ct)[n][m] * co + (*St)[n][m] * si) * P[n][m];//计算重力扰动
		}
	}
	//计算大地水准面高
    N = T / gamma;
	//单位换算mGal
	dg1 = dg1 * 100000.0;
	dg2 = dg2 * 100000.0;
}

3.3 主函数文件

#include"wxf.h"
using namespace std;
int main()
{
	vector<vector<double>>* C = new vector<vector<double>>;
	vector<vector<double>>* S = new vector<vector<double>>;
	vector<vector<double>>* Ct = new vector<vector<double>>;
	vector<vector<double>>* St = new vector<vector<double>>;
	C->resize(361); S->resize(361); Ct->resize(361); St->resize(361);
	for (int i = 0; i < 361; i++)
	{
		(*C)[i].resize(361);
		(*S)[i].resize(361);
		(*Ct)[i].resize(361);
		(*St)[i].resize(361);
	}
	read_Cnm_Snm(C, S);
	calculate_Ct_St(C, S, Ct, St);
	delete C; delete S;
	vector<Zone> *Z1=new vector<Zone>;//全球范围
	vector<Zone> *Z2=new vector<Zone>;//区域范围
	for (int i = 0; i < 180; i++)
	{
		for (int j = 0; j < 361; j++)
		{
			Zone z;
			z.B = -89.5 + i;
			z.L = j * 1.0;
			z.H = 0;
			z.BLH_to_rthetalamda();
			z.calculate_gamma();
			z.calculate_Pnm();
            z.calculate(Ct, St);
			Z1->push_back(z);
		}
	}
	for (int i = 0; i < 361; i++)
	{
		for (int j = 0; j < 361; j++)
		{
			Zone z;
			z.B = 20.0 + i / 12.0;
			z.L = 70.0 + j / 12.0;
			z.H = 0;
			z.BLH_to_rthetalamda();
			z.calculate_gamma();
			z.calculate_Pnm();
			z.calculate(Ct, St);
			Z2->push_back(z);
		}
		cout << i<<endl;
	}
	delete Ct; delete St;
	ofstream outfile1;
	ofstream outfile2;
	outfile1.open("全球范围结果.txt");
	outfile2.open("区域范围结果1.txt"); 
	outfile1 << "   纬度" << "  " << "   经度" << "          " << "扰动位" << "            " << "大地水准面高" << "      " << "重力异常" << "         " << "重力扰动" << endl;
	outfile2 << "   纬度" << "  " << "   经度" << "          " << "扰动位" << "            " << "大地水准面高" << "      " << "重力异常" << "         " << "重力扰动" << endl;
	for (vector<Zone>::iterator it = Z1->begin(); it != Z1->end(); it++)
	{
		outfile1 << setiosflags(ios::fixed) << setprecision(3) << it->B << "  " << it->L << "  " << setprecision(8) << it->T << "  " << it->N << "  " << it->dg1 << "  " << it->dg2 << endl;
	}
	for (vector<Zone>::iterator it = Z2->begin(); it != Z2->end(); it++)
	{
		outfile2 << setiosflags(ios::fixed) << setprecision(3) << it->B << "  " << it->L << "  " << setprecision(8) << it->T << "  " << it->N << "  " << it->dg1 << "  " << it->dg2 << endl;
	}
	outfile1.close();
	outfile2.close();
	delete Z1; delete Z2;
	return 0;
}