超详细的排序算法实现与分析(插入排序，归并排序，快速排序)

最新推荐文章于 2023-12-05 07:49:10 发布

Krito.

最新推荐文章于 2023-12-05 07:49:10 发布

阅读量3.3k

点赞数 7

分类专栏：算法文章标签：排序算法算法数据结构

本文链接：https://blog.csdn.net/qq_62959684/article/details/122117848

版权

算法专栏收录该内容

3 篇文章

订阅专栏

本文详细介绍了比较排序的三大经典算法：插入排序、归并排序和快速排序。包括各自的伪代码、分治思想、时间复杂度分析和正确性证明。特别强调了快速排序在最坏情况和平均情况下的性能，以及在实际应用中的优势。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2.快速排序的正确性（即PARTITION的正确性）

3.快速排序的性能

4.快速排序示意图

快速排序的应用

最好使用电脑阅读本文!!!!!

比较排序

1.比较排序的定义

在排序的最终结果中，各元素的次序依赖于它们之间的比较，我们把这类排序算法称为比较排序。

2.比较排序算法的下界

定理1:在最坏情况下，任何比较排序算法都需要做 $\Omega (nlgn)$ 次比较。

证明:

考虑一颗高度为h，具有L个可达叶节点的决策树，它对应一个对n个元素所做的比较排序(如下图所示）。因为输入数据的n！种可能的排列都是叶节点，所以有n!<=L。由于在一颗高度为h1的二叉树中，叶节点的数目不多于 $2^{n}$ ,所以可以得到：n!<=L<= $2^{n}$ 。对该式两边取对数，有

h>=lg(n!)= $\Omega (nlgn)$

定理2:堆排序和归并排序都是渐进最优的比较排序算法。

证明:堆排序和归并排序的运行时间上界为O(nlgn)，与定理1给出的最坏情况的下界 $\Omega (nlgn)$ 是一致的.

3.常见的比较排序

插入排序（Insertion Sort）、希尔排序（Shell Sort）、快速排序（Quicksort）、冒泡排序（Bubble Sort)，选择排序（Selection Sort）、堆排序（Heap Sort）、归并排序（Merge Sort）、内省排序（Introspective Sort）等。

本文将介绍插入排序，归并排序，快速排序这三种排序算法并给出时间复制度的分析与算法正确性的证明。

插入排序

1.插入排序伪代码

INSERTION-SORT(A)
 for j = 2 to A.length
     key=A[j]
     //将A[j]插入到已排好序的序列A[1..j-1]中。
     i = j - 1
     while i > 0 and A[i] > key
         A[i+1] = A[i]
         i = i - 1
     A[i+1] = key

伪代码为的是满足不同编程语言的需求，如果你熟悉任何一门编程语言，将伪代码变成对应语言是很轻松的事。

2.插入排序演示图

3.插入排序的正确性

初始化:子数组A[1..j-1]仅由单个元素A[1]组成，实际上就是A[1]中原来的元素。而且该子数组是排序好的。这表明第一次循环迭代之前的循环不变式成立。

保持:非形式化地，for循环体的4~7行将A[j-1],A[j-2],A[j-3]等向右移动一个位置，直到找到A[j]的适当位置，第八行将A[j]的值插入该位置。这是子数组A[1..j]由原来在A[1..j]中的元素组成，但已按序排列，那么对for循环的下一次迭代增加j将保持循环不变式。

终止:导致for循环终止的条件是j>A.length=n。因为每次循环迭代j增加1，那么必有j=n+1。在循环不变式的表述中将j用n+1代替，我们有子数组A[1..n]由原来在A[1..n]中的元素组成，但已按序排列。注意到，子数组A[1..n]就是整个数组，我们推断出整个数组已排序。因此算法正确。

4.插入排序算法的分析

INSERTION-SORT(A)         代价次数
for j = 2 to A.length $c_{1}$ n
key=A[j]    $c_{2}$ n - 1
//将A[j]插入到已排好序的序列A[1..j-1]中。 0 n - 1
i = j - 1    $c_{4}$ n - 1
while i > 0 and A[i] > key                                                 $c_{5}$    $\sum$ $t_{j}$ (2~n)
A[i+1] = A[i]    $c_{6}$    $\sum (t_{j}-1)$ (2~n)
i = i - 1                                                                         $c_{7}$                     $\sum (t_{j}-1)$ (2~n)
A[i+1] = key    $c_{8}$ n-1

$T(n)=c_{1}n+c_{2}(n-1)+c_{4}(n-1)+c_{5}\sum_{j=2}^{n}t_{j}+c_{6}\sum_{j=2}^{n}(t_{j}-1)+c_{7}\sum_{j=2}^{n}(t_{j}-1)+c_{8}(n-1)$

最佳情况分析：

若输入数组已排好序，则出现最佳情况。这时，对每个j=2，3，...，n，我们发现在第五行，当i取其初值j-1时，有A[i]<=key。从而对j=2,3,...,n,有 $t_{j}$ =1，该最佳情况的运行时间为:

$T(n)=c_{1}n+c_{2}(n-1)+c_{4}(n-1)+c_{5}(n-1)+c_{8}(n-1)=(c_{1}+c_{2}+c_{4}+c_{5}+c_{8})n-(c_{2}+c_{4}+c_{5}+c_{8})$

它是n的线性函数，最佳情况的运行时间记作 $\Theta (n)$ 。

最坏情况分析：

若输入数据已反向排序，则导致最坏情况。我们必须将每个元素A[j]与整个已排序的子数组A[1..j-1]中的每个元素进行比较，所以对j=2，3，...，n,有 $t_{j}=j$ 。则有

$\sum_{j=2}^{n}j=\frac{n(n+1)}{2}-1$ 和 $\sum_{j=2}^{n}(j-1)=\frac{n(n-1)}{2}$ ,那么对T(n)有

$T(n)=c_{1}n+c_{2}(n-1)+c_{4}(n-1)+c_{5}(\frac{n(n+1)}{2}-1)+c_{6}(\frac{n(n-1)}{2})+c_{7}(\frac{n(n-1)}{2})+c_{8}(n-1)=(\frac{c_{5}}{2}+\frac{c_{6}}{2}+\frac{c_{7}}{2})n^{2}+(c_{1}+c_{2}+c_{4}+\frac{c_{5}}{2}-\frac{c_{6}}{2}-\frac{c_{7}}{2}+c_{8})n$

我们可以把该最坏情况运行时间表示为 $an^{2}+bn+c$ ,记作 $\Theta (n^{2})$ .

归并排序

1.归并排序伪代码

MERGE(A , p , q , r)

1 $n_{1}$ = q - p + 1

2 $n_{2}=r-q$

3 let L[1.. $n_{1}$ +1] and R[1.. $n_{2}$ +1] be new arrays

4 for i = 1 to $n_{1}$

5 L[i] = A[p + i - 1]

6 for j = 1 to $n_{2}$

7 R[j] = A [ q + j ]

8 L[ $n_{1}$ +1] = $\infty$

9 R[ $n_{2}$ +1] = $\infty$

10 i = 1

11 j = 1

12 for k = p to r

13 if L[ i ] <= R[ j ]

14 A[k] = L [ i ]

15 i = i + 1

16 else A[k] = R[j]

17 j = j + 1

MERGE-SORT(A，p，r）

1 if p < r

2 q = (p+r)/2（向下取整)

3 MERGE-SORT(A，p，q）

4 MERGE-SORT(A，q+1，r）

5 MERGE(A，p，q，r）

2.归并算法中的分治思想

分治法：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

分治模式在每层递归时都有三个步骤：

分解原问题为若干子问题，这些子问题是原问题的规模较小的实例。

解决这些子问题，递归地求解各子问题。若子问题的规模足够小，则直接求解。

合并这些子问题的解成原问题的解。

归并排序的分治模式：

分解: 分解待排序的n个元素的序列成各具n/2个元素的子序列。

解决：使用归并排序递归地排序两个子序列。

合并：合并两个已排序的子序列以产生已排序的答案。

3.归并排序演示图

MERGE过程演示

归并排序演示

4.MERGE过程的正确性

初始化：循环的第一次迭代之前，有k = p，所以子数组A[p..k-1]为空。这个空的子数组包含L和R的k-p=0个最小元素。又因为i=j=1，所以L[i]和R[j]都是各自所在数组中未被复制回数组A的最小元素。

保持：假设L[i]<=R[j]。这时，L[i]是未被复制回数组A的最小元素。因为A[p..k-1]包含k-p个最小元素，所以在第14行将L[i]复制到A[k]之后，子数组A[p..k]将包含k-p+1个最小元素。增加k的值和i的值后，为下次迭代重新建立了该循环不变式。反之，若L[i]>R[j]，则第16~17行执行适当的操作来维持该循环不变式。

终止：终止时k=r+1。根据循环不变式，子数组A[p..k-1]就是A[p..r]且按从小到大的顺序包含L[1.. $n_{1}$ +1]和R[1.. $n_{2}$ +1]中的k-p=r-p+1个最小元素。数组L和R一起包含 $n_{1}+n_{2}+2=r-p+3$ 个元素。除两个最大的元素以外，其他所有元素都已被复制回数组A，这两个最大元素就是哨兵。

5.归并排序算法的分析

T(n)的递归式

当有n>1个元素时（为方便起见，假设n刚好是2的幂），我们分解运行时间如下:

分解：分解步骤仅计算子数组的中间位置，因此为 $\Theta (1)$ 。

解决：递归地求解两个规模均为n/2的子问题，将贡献2T(n/2)的运行时间。

合并：在一个具有n个元素的子数组上过程MERGE需要 $\Theta (n)$ 的时间。

有T(n) = $\left\{\begin{matrix}\Theta (1) & n=1 & \\ 2T(n/2)+\Theta (n) & n>1 & \end{matrix}\right.$ = $\Theta (nlgn)$

递归式的求解

（图的方向可能有问题，下载下来后旋转一下）

快速排序

快速排序可以说是在算法竞赛中使用的最多的一种排序算法，它的期望时间复杂度是 $\Theta (nlgn)$ ，且隐含的常数因子非常小，大多数情况下能达到该时间复杂度，最坏情况下的时间复杂度为 $\Theta (n^{2})$ ，它还是一种原址排序。

1.快速排序的描述

快速排序中的分治思想:

分解：数组A[p..r]被划分成两个子数组A[p..q-1]和A[q+1，r]，使得A[p..q-1]中的每一个元素都小于等于A[q]，而A[q]也小于等于A[q+1..r]中的每个元素，其中，计算下标q也是划分过程的一部分

解决：通过递归调用快速排序，对子数组A[p..q-1]和A[q+1,r]进行排序。

合并：因为子数组都是原址排序的，所以不需要合并操作：数组A[p..r]已经有序。

快速排序代码(C++实现)

#include<bits/stdc++.h>
using namespace std;
int n,k=1;
int PARTITION(int* a, int, int);
void QUICKSORT(int* a, int p, int r) {
	if (p < r) {
		int q = PARTITION(a, p, r);
		QUICKSORT(a, p, q - 1);
		QUICKSORT(a, q + 1, r);
	}
	return;
}
void print(int* a);
int PARTITION(int* a, int p, int r) {
	int x = a[r];
	int i = p - 1;
	for (int j = p; j <= r - 1; j++) {
		if (a[j] <= x) {
			i = i + 1;
			int temp = a[i];
			a[i] = a[j];
			a[j] = temp;
		}
	}
	int temp = a[i + 1];
	a[i+1] = a[r];
	a[r] = temp;
	print(a);
	return i + 1;
}
void print(int* a) {
	cout << "第" << k << "次PARTITION后的数组: ";
	for (int i = 0; i < n; i++) cout << a[i];
	k++;
	cout << endl;
}
int main() {
	int a[10000];
	cout << "请输入待排序数据的规模: " << endl;
	cin >> n;
	cout << "请输入" << n << "个数据：" << endl;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	QUICKSORT(a, 0, n-1);
}

（为了能更直观的展示快速排序过程，故代码加入了提示输入，输出语句）

PARTITION总是选择一个x=A[r]作为主元，并围绕它来划分子数组A[p..r]。随着程序的进行，数组被划分成4个（可能有空的）区域。在PARTITION中循环体的每一轮迭代开始时，对于任意数组下标k，有：

1.若p<=k<=i,则A[k]<=x。

2.若i+1<=k<=j-1,则A[k]>x。

3.若k=r，则A[k]=x。

4.若j<=k<=r-1,对应位置的值于主元不存在特定的大小关系。

PARTITION维护的正是这四个区域。

2.快速排序的正确性（即PARTITION的正确性）

初始化：在循环的第一轮迭代开始之前，i=p-1和j=p。因为在p和i之间、i+1和j-1之间都不存在值，所以循环不变量的两个条件显然都满足。第1行中的赋值操作满足了第三个条件。

保持：考虑两种情况。当A[j]>x时的情况：循环体的唯一操作是j的值加1。在j值增加后，对A[j-1]，条件2成立，且所有其他项都保持不变。当A[j]<=x是的情况：将i值加1，交换A[i]和A[j]，再将j值加1.因为进行了交换我，现在有A[I]<=x，所以条件1得到满足。类似地，我们也能得到A[j-1]>x。因为根据循环不变量，被交换进A[j-1]的值总是大于x的。

终止：当终止时，j=r。于是，数组中的每个元素都必然属于循环不变量中所描述的三个集合中的一个，也就是说，我们已经将数组中的所有元素划分成了三个集合：包含了所有小于等于x的元素的集合、包含了所有大于x的元素的集合和只有一个元素x的集合。

在PARTITION的最后两行中，通过将主元于最左的大于x的元素进行交换，就可以将主元移到它在数组中的正确位置上，并返回主元的新下标。此时，PARTITION的输出满足划分步骤规定的条件。PARTITION在子数组A[p..r]上的时间复杂度是 $\Theta (n)$ ,其中n=r-p+1.

3.快速排序的性能

最坏情况划分

当划分产生的两个子问题分别包含了n-1个元素和0个元素时，快速排序的最坏情况产生了。假设算法的每一次递归调用中都出现了这种不平衡划分。划分操作的时间复杂度是 $\Theta (n)$ 。由于对一个大小为0的数组进行递归调用会直接返回，因此T(0)= $\Theta(1)$ 。于是算法运行时间的递归式可以表示为： $T(n)=T(n-1)+T(0)+\Theta (n)=T(n-1)+\Theta (n)$ .这个递归式的解为T(n)= $\Theta (n^{2})$

最好情况划分

当划分产生的两个子问题的规模都不大于n/2时，快速排序的性能非常好。此时，算法运行时间的递归式为： $T(n)=2T(n/2)+\Theta (n)$ 该递归式的解为T(n)= $\Theta (nlgn)$ 。通过在每一层递归中都平衡划分子数组，我们得到了一个渐进时间上更快的算法。

平均情况的直观观察

假设好和差的划分交替出现在数的各层上，并且好的划分是最好情况划分，而差的划分是最坏情况的划分，如下图所示。在根节点处，划分的代价为n，划分产生的两个子数组的大小为n-1和0，即最坏情况。在下一层上，大小为n-1的子数组按最好情况划分成大小分别为(n-1)/2-1和(n-1)/2的子数组。在这里，我们假设大小为0的子数组的边界条件代价为1。

在一个差的划分后面接着一个好的划分，这种组合产生出三个子数组，大小分别为0，( n-1)/2-1和(n-1)/2。这一组合的划分代价为 $\Theta (n)+\Theta (n-1)=\Theta (n)$ 。该代价并不比b图中的划分更差。在图b中，一层划分就产生出大小为(n-1)/2的两个子数组，划分代价为 $\Theta (n)$ 。从直观上看，差划分的代价 $\Theta (n-1)$ 可以被吸收到好划分的代价 $\Theta (n)$ 中去，而得到的划分结果也是好的。因此，当好和差的划分交替出现时，快速排序的时间复杂度与全是好的划分时一样，仍然是O(nlgn)。区别只是O符号中隐含的常数因子略大一些。

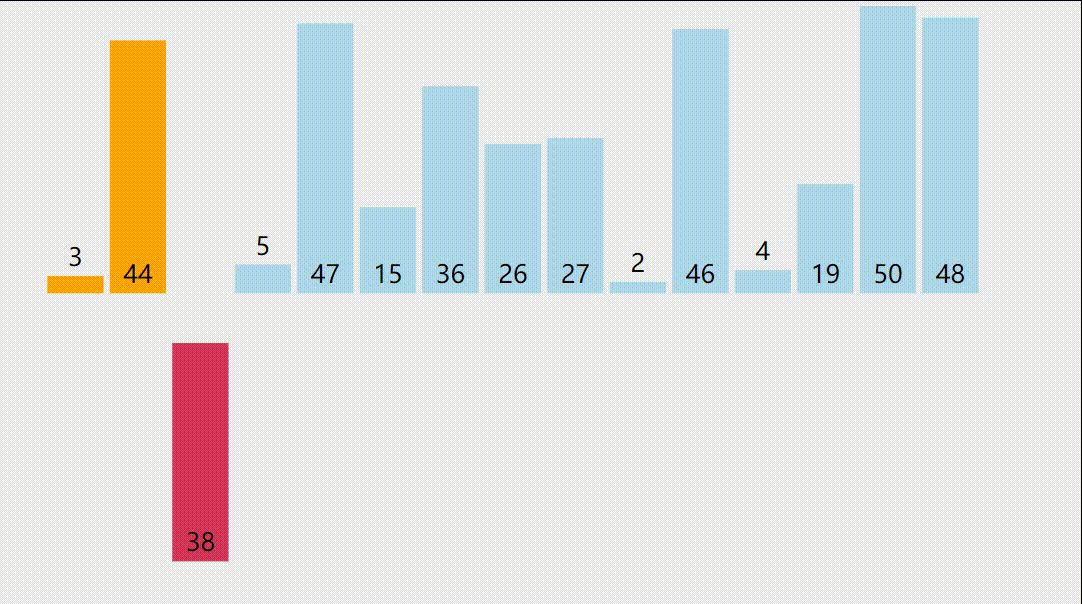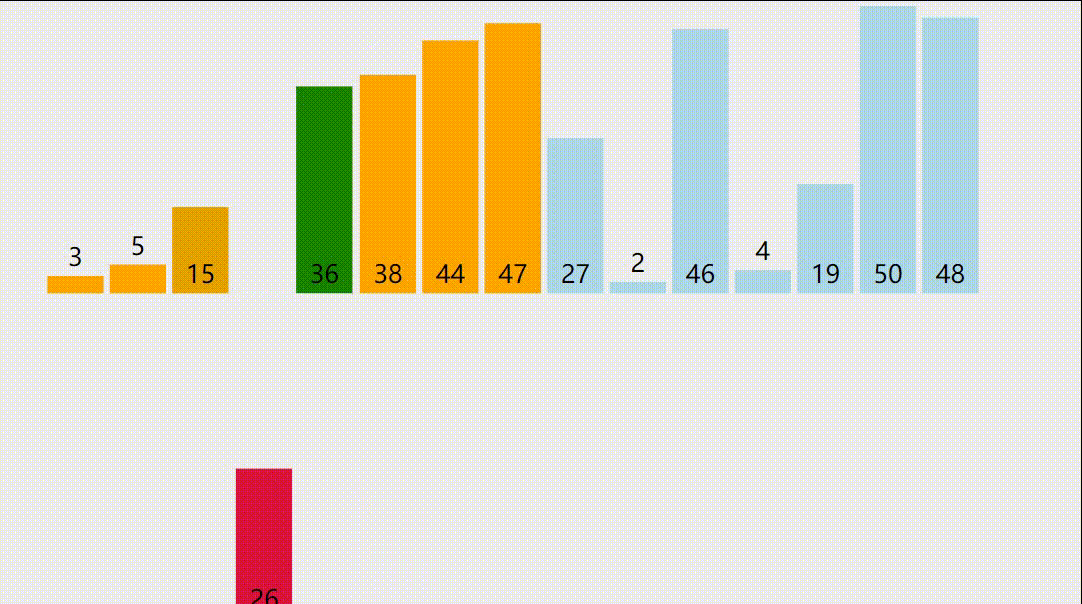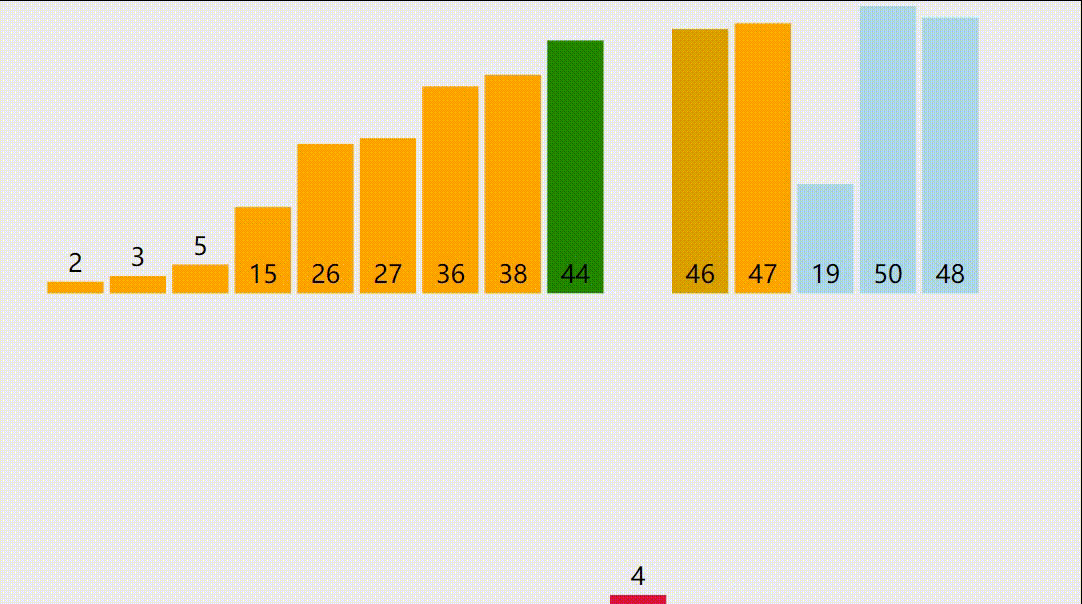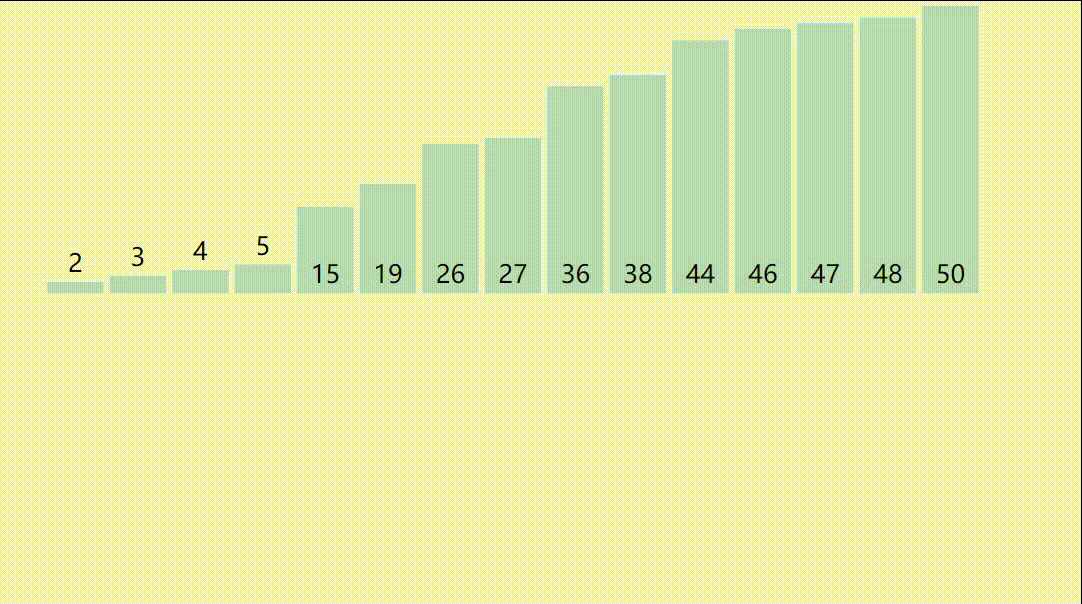
4.快速排序示意图

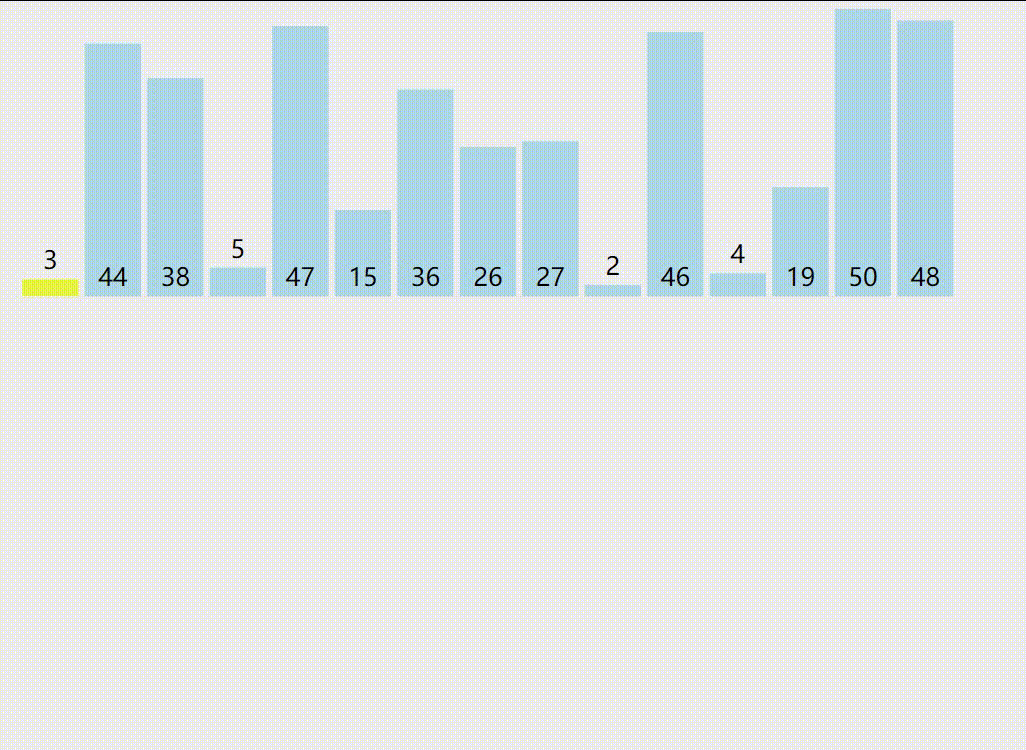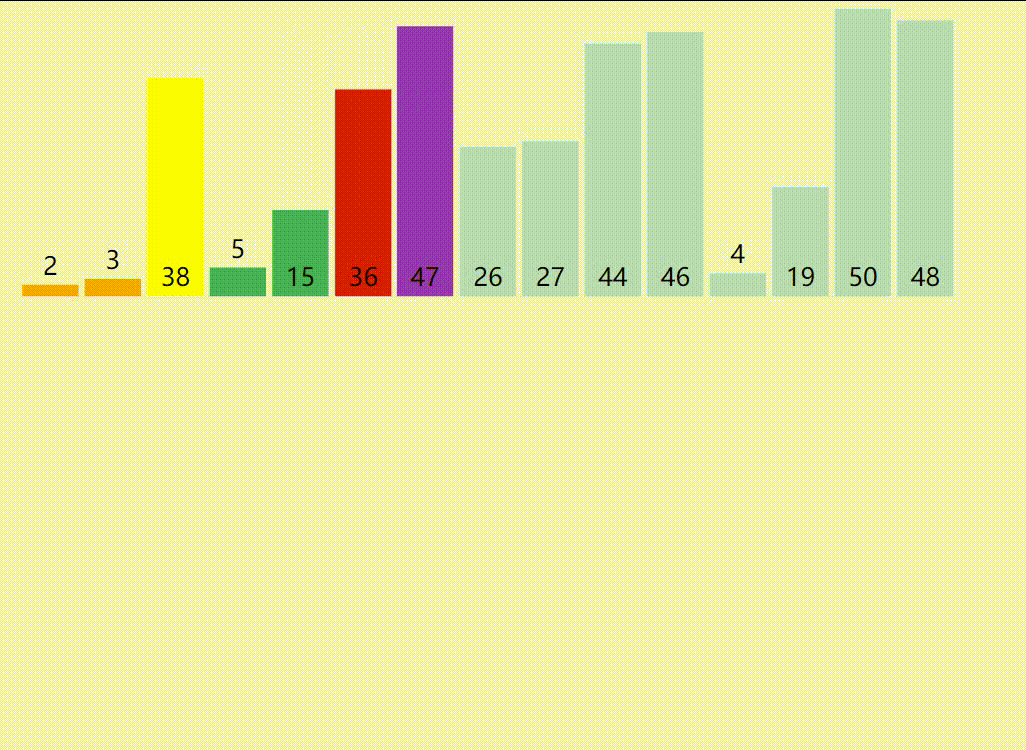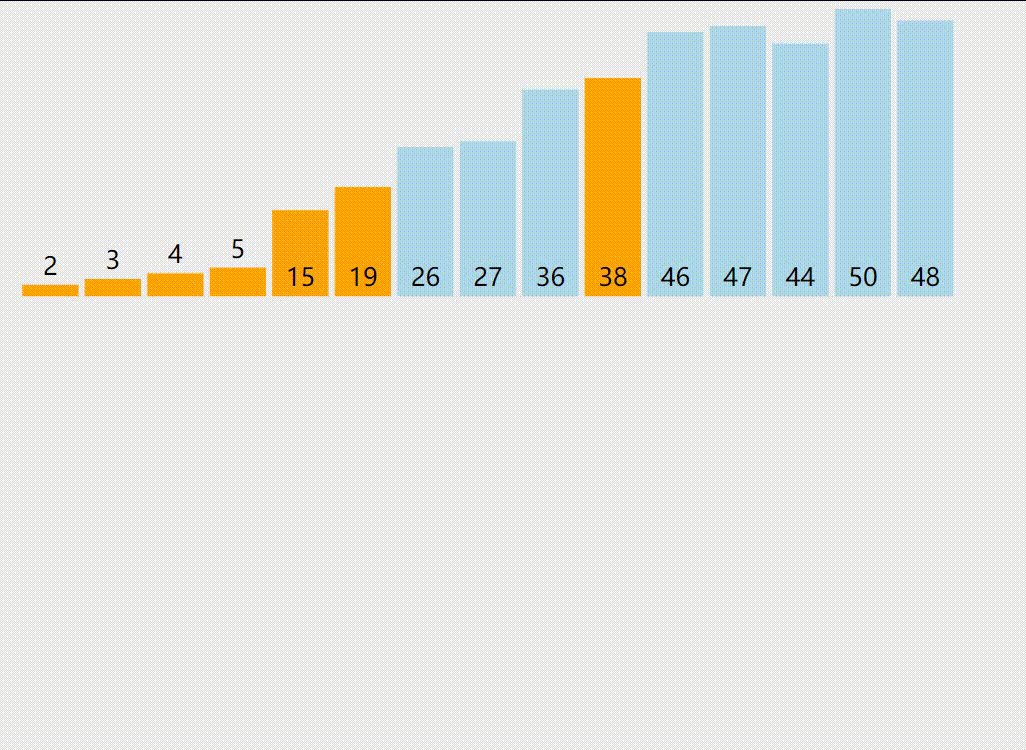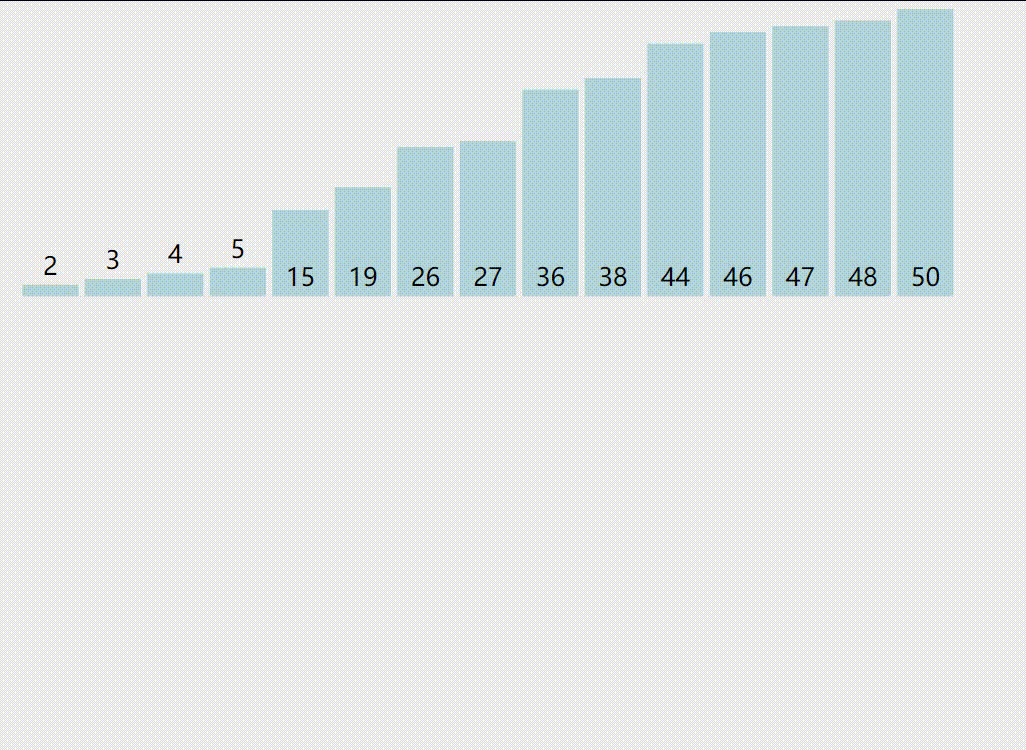
黄色标识的数字是PARTITION过程的主元。紫色和绿色分别为大于主元的区间和小于等于主元的区间。红色是正在与主元比较的元素。蓝色是待比较的元素。希望您能看懂。

———————————————————————————————————————————

快速排序的应用

这三种排序算法中最为实用的便是快速排序（竞赛中），你可能觉得在c++的stl中已经替你实现了该算法便不在需要深入了解，但有些题目恰恰捉住了这一点，如果对快速排序的原理，也就是分治法没有深入的了解，在面对这样的题目的时候就会无能为力，在这里给出一例，希望我们快排和分治算法有更深层的应用。

求第k小的数。

输入n（1<=n<5000000且n为奇数)个数字 $a_{i}$ （1<= $a_{i}$ < $10^{9}$ ),输出这些数字的第k小的数。

最小的数是第0小。

如果你只会sort后输出第k个数，那么这题会tle，因为时间复杂度为O(nlgn)。而这题要求设计一个O(n)的算法来达到目的。

我们要找第k小，而直接sort是排序整个数组。我们每次递归会排序上一次递归返回的下标的两侧的数组，在此我们可以优化一下，如果该下标等于k则直接输出并停止排序；如果改下标大于k则排序该下标左侧的数组即可；如果该下标小于k，则排序该下标右侧的数组即可。

经过这样的优化后，时间复杂度降到了O(n)。

~~(其实这道题也可以用stl中提供的函数解决）。~~

AC代码

#include<bits/stdc++.h>
using namespace std;
int s[5000000];
void quick_sort( int l, int r,int k)
{
        int i = l, j = r, x = s[l];
        while (i < j)
        {
            while (i < j && s[j] >= x) // 从右向左找第一个小于x的数
                j--;
                s[i] = s[j];

            while (i < j && s[i] < x) // 从左向右找第一个大于等于x的数
                i++;
                s[j] = s[i];
        }
        s[i] = x;
        if (k == i) {
            cout << s[i];
            return;
        }
        else if(k<i)
        quick_sort( l, i - 1,k); // 递归调用 
        else if(k>i)
        quick_sort( i + 1, r,k);
}
int main() {
	int n, k;
	cin >> n >> k;
	for (int i = 0; i < n; i++) {
        scanf("%d",&s[i]);
	}
	quick_sort(0, n - 1, k);
}

如有错误，欢迎指出。如果对您有帮助，可以点个赞鼓励一下我。本人水平尚浅，日后可能会完善改文章。(比如补全比较排序的其他算法）