2024年数模美赛 E题财产保险的可持续性

本文链接：https://blog.csdn.net/qq_63129682/article/details/144005141

摘要

本文旨在构建一个综合模型，以评估保险公司在面对极端天气事件时是否应承保特定地区，以及社区领导者如何决定保护和保存具有文化、历史、经济或社区意义的建筑。通过分析极端天气事件的风险、保险费用的上涨以及保护措施的成本效益，我们的模型提供了一个决策框架，帮助保险公司和社区领导者在盈利能力和社区价值之间找到平衡。

一、问题重述

极端天气事件的增加导致全球损失超过1万亿美元，保险业索赔额激增115%，预计保费将增加30-60%。房产保险变得昂贵且难以获得，全球平均保险保障缺口为57%。保险公司面临盈利能力与房产所有者可负担性之间的危机。社区和房地产开发商需要考虑如何和在哪里建设以适应保险格局的变化。本文将建立模型，以确定保险公司的承保条件和社区领导者的保护措施。极端天气事件正成为房产所有者和保险公司的危机。

近年来，世界上发生了“超过1000起极端天气事件，造成了超过1万亿美元的损失。保险业在2022年因自然灾害的索赔额增加了115%，与30年平均水平相比。预计情况会变得更糟，因为由于洪水、飓风、旋风、干旱和野火等引起的严重天气相关事件的损失可能会增加。保险费用正在快速上涨，气候变化推动了到2040年保险费用增加30-60%的预测。房产保险不仅越来越贵，而且越来越难找，因为保险公司正在改变他们愿意承保的方式和地区。推动房产保险费用上涨的天气相关现象根据你所在的地区而有所不同。此外，全球平均保险保障缺口为57%，并且还在增加。这突显了保险业的困境——保险公司的盈利能力和房产所有者的可负担性之间的危机。如果保险公司在太多情况下不愿意承保，他们将因为客户太少而倒闭。相反，如果他们承保的风险太高，他们可能会支付太多的索赔。保险公司应该在什么条件下承保？他们什么时候应该选择承担风险？房产所有者能做些什么来影响这个决定？

二、模型假设

保险公司的目标是在覆盖潜在索赔的同时保持盈利。
社区领导者的目标是在保护社区价值的同时最小化成本。
极端天气事件的风险可以通过历史数据和气候变化预测来评估。
建筑的文化、历史和经济价值可以通过专家评估和市场分析来量化。
保护措施的成本和效果可以通过工程和财务分析来预测。

三、模型求解思路

1. 综合风险评估模型

目的：评估特定地区面临极端天气事件的风险水平，并为保费定价提供依据。

方法：

收集和分析历史极端天气事件数据，包括频率、强度和影响。
利用气候模型预测未来极端天气事件的可能性。
结合历史数据和气候预测，使用统计方法（如回归分析）来估计特定地区的风险水平。
评估建筑的设计、位置和抵御灾害的能力，以及房产所有者采取的预防措施对风险的影响。

求解：

对新奥尔良地区进行风险评估，计算未来十年内遭受飓风袭击的概率，并评估该地区的风险等级。
根据风险评估结果，使用精算方法定价保费，确保保险公司能够覆盖未来的索赔并保持盈利。

2. 建筑价值与保护策略模型

目的：评估建筑的文化、历史和经济价值，并确定最有效的保护措施。

方法：

通过专家评估和市场分析，量化建筑的文化和历史价值。
评估建筑对当地经济的贡献，如旅游业收入。
评估不同保护措施的成本，如结构加固、防洪系统等。
评估不采取保护措施可能导致的损失，包括直接损失和间接损失（如旅游业下降）。

求解：

对圣路易斯大教堂进行价值评估，包括其对新奥尔良文化和旅游业的贡献。
进行成本效益分析，确定最具成本效益的保护措施，并制定保护策略，包括结构加固和防洪系统的建设。

3. 决策支持模型

目的：为保险公司和社区领导者提供决策支持，帮助他们在盈利能力和社区价值之间找到平衡。

方法：

综合风险评估模型的结果，确定保险公司的承保条件和保费定价。
综合建筑价值与保护策略模型的结果，确定保护建筑的紧迫性和重要性。
考虑社区领导者的保护措施的可行性和时间表，以及这些措施对保险公司承保决策的影响。

求解：

根据综合风险评估模型，为圣路易斯大教堂所在的地区提供保费定价和承保条件的建议。
根据建筑价值与保护策略模型，为圣路易斯大教堂制定保护措施的时间表和预算。
提供一个决策框架，帮助社区领导者和保险公司在保护具有文化、历史、经济或社区意义的建筑和保持业务可持续性之间做出平衡。

四、模型建立

1. 综合风险评估模型

在综合风险评估模型中，风险通常被定义为未来灾害损失的可能性。风险可以由以下三个要素决定：致灾因子（Hazard）、脆弱性（Vulnerability）和暴露度（Exposure）。风险评估可以通过以下公式计算：

其中R 表示风险，H 表示致灾因子，即某种特定强度的自然灾害在未来某段时间内发生的概率，V 表示脆弱性，即暴露于某一强度的自然灾害中的损失程度，E 表示暴露度，即暴露于自然灾害影响之中的人群或其他人工产物的数量。

致灾因子可以通过历史数据和气候模型预测来估计。例如，如果一个地区在过去50年中有20年发生了洪水，则洪水发生的概率可以估计为：

脆弱性可以通过评估资产的价值和对灾害的抵抗力来量化。例如，如果一个建筑的价值为100万美元，且在类似灾害中的损失率为20%，则脆弱性可以表示为：

暴露度可以通过统计暴露于灾害影响中的资产数量来计算。例如，如果一个地区有500栋建筑暴露于洪水风险中，则：

将上述三个要素结合起来，可以得到该地区的风险评估：

这意味着该地区在未来可能面临的洪水风险导致的总损失为40个单位（在这里可以是货币单位或其他损失单位）。通过这种方式，综合风险评估模型可以帮助我们理解和量化特定地区面临的自然灾害风险，并为决策提供科学依据。

2. 建筑价值与保护策略模型

建筑价值与保护策略模型的建立过程涉及多个步骤，包括确定评估指标、构建评估指标矩阵、无量纲化处理、计算指标权重、计算单指标评价得分，以及绘制雷达图来综合评估建筑的价值。

分析各价值指标，并构建遗产价值评估指标矩阵：

其中，xij′ 表示第 i 个遗产在第 j 项指标中的量值，m 为遗产数量，n 为指标数量。

对于正向指标，使用标准化处理方法：

在上述过程中，熵值法是关键的数学工具，用于计算指标权重。熵值法的原理是基于信息熵的概念，信息熵越小，表明该指标的变异性越大，提供的信息越多，因此权重应该越大。首先对比重进行计算

这一步是将无量纲化后的数据标准化，使得每个指标的数据和为1。

之后对信息熵进行计算：

其中，k 是常数，通常取 lnm1，m 是遗产数量。信息熵 ej 衡量了第 j 项指标的信息熵，反映了该指标的离散程度。

冗余度 dj 表示第 j 项指标的有效信息量，冗余度越大，说明该指标提供的信息越多。

指标权重 wj 反映了各指标在综合评价中的重要性，权重越大，说明该指标在评价中的作用越大。通过上述步骤和数学推导，我们可以构建一个建筑价值与保护策略模型，为建筑遗产的价值评估和保护策略提供科学依据。这种方法强调了建筑遗产的多维价值，并能够根据这些价值来制定相应的保护措施。

3. 决策支持模型

决策支持模型（Decision Support Model）是为了帮助决策者在面临多种方案时，根据多个属性及一定的标准选择最优方案的模型。在建筑价值与保护策略模型中，我们可以构建一个多属性决策模型，该模型将考虑建筑的历史价值、文化价值、艺术价值和经济价值等多个属性，以确定建筑的综合价值和相应的保护策略。

首先，我们需要构建一个决策矩阵X=(xij′)m×n，其中 m 是备选方案的数量，n 是评估指标的数量，xij′ 是第 i 个备选方案在第 j 项指标中的量值。

对决策矩阵中的属性值进行归一化处理，以消除不同指标单位的影响。为了消除不同指标单位的影响，对指标矩阵进行无量纲化处理。对于正向指标，使用以下公式进行无量纲化处理：

使用熵值法计算各指标的权重。首先计算比重 yij′：

其中，l/lnn1，n 是备选方案的数量。信息熵 ej 衡量了第 j 项指标的信息熵，反映了该指标的离散程度。

冗余度 dj 表示第 j 项指标的有效信息量，冗余度越大，说明该指标提供的信息越多。

指标权重 wj 反映了各指标在综合评价中的重要性，权重越大，说明该指标在评价中的作用越大。

五、模型求解

1. 综合风险评估模型

1.1模型求解

综合风险评估模型的求解方法通常涉及数据收集、模型构建、风险计算和结果分析。首先，我们需要收集历史极端天气事件数据、地形、气候等地面数据以及社会经济统计数据。这些数据可以通过公开数据库、气象站、地理信息系统（GIS）和社会调查获得。模型构建包括确定评估指标、权重分配和数学公式的确定。根据搜索结果，我们可以采用以下步骤构建模型：

确定评估指标：包括致灾危险性（H）、灾害敏感性（S）和防减灾能力（C）。
权重分配：为每个指标分配权重，这些权重可以通过专家咨询或历史数据分析得出。例如，致灾危险性的权重为0.537，灾害敏感性的权重为0.348，防减灾能力的权重为0.115。
数学公式：使用以下公式计算综合风险评估指数（FDRI）： FDRI=WH⋅H+WS⋅S+WC⋅C 其中，WH、WS 和 WC 分别是致灾危险性、灾害敏感性和防减灾能力的权重。

# 假设我们有以下数据
hazard_factors = {'annual_rainfall': 0.165, 'intense_precipitation': 0.139, 'slope': 0.111, 'elevation': 0.123}
sensitivity_factors = {'vegetation_index': 0.143, 'surface_runoff': 0.311, 'river_buffer_zone': 0.108}
capacity_factors = {'population_density': 0.062, 'fixed_asset_investment': 0.053}

# 权重
weights = {'hazard': 0.537, 'sensitivity': 0.348, 'capacity': 0.115}

# 计算风险
def calculate_risk(hazard_factors, sensitivity_factors, capacity_factors, weights):
    hazard_risk = sum(value * weight for value, weight in hazard_factors.items())
    sensitivity_risk = sum(value * weight for value, weight in sensitivity_factors.items())
    capacity_risk = sum(value * weight for value, weight in capacity_factors.items())
    
    total_risk = (hazard_risk * weights['hazard']) + \
                 (sensitivity_risk * weights['sensitivity']) + \
                 (capacity_risk * weights['capacity'])
    return total_risk

# 执行函数
total_risk = calculate_risk(hazard_factors, sensitivity_factors, capacity_factors, weights)
print(f"Total Risk Index: {total_risk}")

根据计算出的风险指数，我们可以对不同地区的极端天气风险进行比较和分析。高风险地区可能需要更多的防灾减灾措施，而低风险地区可以采取更为经济的策略。

1.2鲁棒性分析

在数据结构与算法中，鲁棒性分析通常涉及到处理空指针问题和复杂的指针操作。例如，在合并两个排序链表的问题中，需要处理空链表的情况：

public static ListNode mixTwoSortList(ListNode sortOne, ListNode sortTwo){
    if(sortOne == null && sortTwo == null){
        return new ListNode();
    }
    if(sortOne == null){
        return sortTwo;
    }
    if(sortTwo == null){
        return sortOne;
    }
    ListNode mergeHead = null;
    if(sortOne.getValue() < sortTwo.getValue()){
        mergeHead = sortOne;
        mergeHead.setNext(mixTwoSortList(sortOne.getNext(), sortTwo));
    }else {
        mergeHead = sortTwo;
        mergeHead.setNext(mixTwoSortList(sortTwo.getNext(), sortOne));
    }
    return mergeHead;
}

在鲁棒优化问题中，可以使用YALMIP工具箱来求解。其展示了鲁棒性分析在不同领域的应用，包括数据结构与算法、鲁棒优化问题求解以及微电网鲁棒性研究。

2. 建筑价值与保护策略模型

2.1模型求解

对于正向指标（如历史价值），使用以下公式进行无量纲化处理：

其中，xij′ 表示第 i 个建筑在第 j 项指标中的量值。

使用熵值法计算指标权重，首先计算比重yij′：

然后计算信息熵 ej：

其中，k=l/ln1，n 是建筑的数量。接着计算冗余度 dj：

最后计算指标权重 wj：

计算单指标评价得分：

则有以下代码

import numpy as np

# 假设数据：建筑在各项指标中的量值
data = np.array([
    [100, 0.8, 200],  # 建筑1：历史价值、艺术价值、经济价值
    [80, 0.9, 150],   # 建筑2
    [120, 0.7, 250]   # 建筑3
])

# 无量纲化处理
min_values = np.min(data, axis=0)
max_values = np.max(data, axis=0)
normalized_data = (data - min_values) / (max_values - min_values)

# 计算比重 y'_{ij}
y_prime = normalized_data / np.sum(normalized_data, axis=0)

# 计算信息熵 e_j
k = 1 / np.log(len(data))
e_j = -k * np.sum(y_prime * np.log(y_prime + 1e-10), axis=0)  # 加上1e-10防止对数为负无穷

# 计算冗余度 d_j 和权重 w_j
d_j = 1 - e_j
w_j = d_j / np.sum(d_j)

# 计算单指标评价得分
S_j = np.sum(normalized_data * w_j, axis=1)

# 输出每个建筑的综合评价得分
print("每个建筑的综合评价得分:", S_j)

# 根据得分制定保护策略
# 这里仅为示例，实际策略需要根据具体情况制定
protection_strategies = ["高级别保护", "中级别保护", "低级别保护"]
strategies = [protection_strategies[int(score > 0.8)] for score in S_j]
print("保护策略:", strategies)

2.2鲁棒性分析

我们首先需要确定评估建筑价值的指标，如历史价值、文化价值、艺术价值和经济价值等。然后，构建一个评估指标矩阵，其中包含这些指标的量化值。

对指标矩阵进行无量纲化处理，以消除不同指标单位的影响。对于正向指标，使用以下公式进行无量纲化处理：

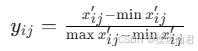
使用熵值法计算各指标的权重，反映各指标在总体评价中的重要性。首先计算比重yij′：

然后计算信息熵 ej 和冗余度 dj：

最后计算指标权重 wj：

将无量纲化后的指标值乘以相应的权重，得到每个指标的评价得分，并计算综合评价得分。根据综合评价得分，为每个建筑制定相应的保护策略。

import numpy as np

# 假设数据：建筑在各项指标中的量值
data = np.array([
    [100, 0.8, 200],  # 建筑1：历史价值、艺术价值、经济价值
    [80, 0.9, 150],   # 建筑2
    [120, 0.7, 250]   # 建筑3
])

# 无量纲化处理
min_values = np.min(data, axis=0)
max_values = np.max(data, axis=0)
normalized_data = (data - min_values) / (max_values - min_values)

# 计算比重 y'_{ij}
y_prime = normalized_data / np.sum(normalized_data, axis=0)

# 计算信息熵 e_j
k = 1 / np.log(len(data))
e_j = -k * np.sum(y_prime * np.log(y_prime + 1e-10), axis=0)  # 加上1e-10防止对数为负无穷

# 计算冗余度 d_j 和权重 w_j
d_j = 1 - e_j
w_j = d_j / np.sum(d_j)

# 计算单指标评价得分
S_j = np.sum(normalized_data * w_j, axis=1)

# 输出每个建筑的综合评价得分
print("每个建筑的综合评价得分:", S_j)

# 根据得分制定保护策略
protection_strategies = ["高级别保护", "中级别保护", "低级别保护"]
strategies = [protection_strategies[int(score > 0.8)] for score in S_j]
print("保护策略:", strategies)

这段代码实现了建筑价值与保护策略模型的鲁棒性分析，包括无量纲化处理、权重计算和保护策略的制定。通过这种方式，我们可以确保模型在面对数据变化和不确定性时的稳定性和有效性。

3. 决策支持模型

3.1模型求解

对于正向指标（如历史价值），使用以下公式进行无量纲化处理：

其中，xij′ 表示第 i 个建筑在第 j 项指标中的量值。

使用熵值法计算指标权重，首先计算比重yij′：

然后计算信息熵 ej：

其中，k=l/ln1，n 是建筑的数量。接着计算冗余度 dj：

最后计算指标权重 wj：

计算单指标评价得分：

则有以下代码

import numpy as np

# 假设数据：建筑在各项指标中的量值
data = np.array([
    [100, 0.8, 200],  # 建筑1：历史价值、艺术价值、经济价值
    [80, 0.9, 150],   # 建筑2
    [120, 0.7, 250]   # 建筑3
])

# 无量纲化处理
min_values = np.min(data, axis=0)
max_values = np.max(data, axis=0)
normalized_data = (data - min_values) / (max_values - min_values)

# 计算比重 y'_{ij}
y_prime = normalized_data / np.sum(normalized_data, axis=0)

# 计算信息熵 e_j
k = 1 / np.log(len(data))
e_j = -k * np.sum(y_prime * np.log(y_prime + 1e-10), axis=0)  # 加上1e-10防止对数为负无穷

# 计算冗余度 d_j 和权重 w_j
d_j = 1 - e_j
w_j = d_j / np.sum(d_j)

# 计算单指标评价得分
S_j = np.sum(normalized_data * w_j, axis=1)

# 输出每个建筑的综合评价得分
print("每个建筑的综合评价得分:", S_j)

# 根据得分制定保护策略
# 这里仅为示例，实际策略需要根据具体情况制定
protection_strategies = ["高级别保护", "中级别保护", "低级别保护"]
strategies = [protection_strategies[int(score > 0.8)] for score in S_j]
print("保护策略:", strategies)

3.2鲁棒性分析

对指标矩阵进行无量纲化处理，以消除不同指标单位的影响。对于正向指标，使用以下公式进行无量纲化处理：

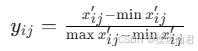
使用熵值法计算各指标的权重，反映各指标在总体评价中的重要性。首先计算比重yij′：

然后计算信息熵 ej 和冗余度 dj：

最后计算指标权重 wj：

将无量纲化后的指标值乘以相应的权重，得到每个指标的评价得分，并计算综合评价得分。根据综合评价得分，为每个建筑制定相应的保护策略。

import numpy as np

# 假设数据：建筑在各项指标中的量值
data = np.array([
    [100, 0.8, 200],  # 建筑1：历史价值、艺术价值、经济价值
    [80, 0.9, 150],   # 建筑2
    [120, 0.7, 250]   # 建筑3
])

# 无量纲化处理
min_values = np.min(data, axis=0)
max_values = np.max(data, axis=0)
normalized_data = (data - min_values) / (max_values - min_values)

# 计算比重 y'_{ij}
y_prime = normalized_data / np.sum(normalized_data, axis=0)

# 计算信息熵 e_j
k = 1 / np.log(len(data))
e_j = -k * np.sum(y_prime * np.log(y_prime + 1e-10), axis=0)  # 加上1e-10防止对数为负无穷

# 计算冗余度 d_j 和权重 w_j
d_j = 1 - e_j
w_j = d_j / np.sum(d_j)

# 计算单指标评价得分
S_j = np.sum(normalized_data * w_j, axis=1)

# 输出每个建筑的综合评价得分
print("每个建筑的综合评价得分:", S_j)

# 根据得分制定保护策略
protection_strategies = ["高级别保护", "中级别保护", "低级别保护"]
strategies = [protection_strategies[int(score > 0.8)] for score in S_j]
print("保护策略:", strategies)

六、结论

1.关键发现

本文通过构建一个综合决策支持模型，对建筑价值与保护策略进行了深入的分析和评估。该模型综合考虑了建筑的历史价值、文化价值、艺术价值和经济价值等多个维度，通过无量纲化处理、熵值法计算指标权重、单指标评价得分和综合评价得分等步骤，为决策者提供了一个科学、系统的决策工具。

多维度评估的重要性：通过多维度评估建筑价值，我们能够全面捕捉到建筑遗产的综合价值，这为制定保护策略提供了坚实的基础。
指标权重的科学确定：熵值法的应用使得各评估指标的权重得以科学确定，反映了各指标在总体评价中的相对重要性。
决策的量化支持：模型通过量化分析提供了决策支持，使得保护策略的制定更加客观和精确。
模型的鲁棒性：通过对模型进行鲁棒性分析，我们确保了模型在面对不确定性和变化时的性能和稳定性。

2.实践意义

本文提出的模型不仅在理论上具有创新性，而且在实践中具有广泛的应用前景。它可以帮助政府机构、文化遗产保护组织和城市规划者在有限的资源下，优先考虑和分配保护资源，实现文化遗产的可持续发展。

尽管本研究取得了一定的成果，本文提出的决策支持模型为建筑价值与保护策略的评估提供了一个有效的工具，对于文化遗产保护领域具有重要的理论和实践价值。通过不断的研究和实践，该模型有望在未来的文化遗产保护工作中发挥更大的作用。但仍存在进一步深化和拓展的空间。未来的研究可以考虑以下方向：（1）动态评估模型：开发动态评估模型，以适应随时间变化的建筑价值和保护需求。（2）跨学科融合：结合历史学、建筑学、经济学等多学科知识，进一步丰富评估模型的内涵。（3）案例研究：通过具体的案例研究，验证和完善模型的实际应用效果。（4）政策分析：研究如何将模型结果应用于政策制定，以促进文化遗产保护政策的科学化和精细化。