实验三 基于MATLAB的离散时间信号的频域分析

实验三 基于MATLAB的离散时间信号的频域分析

一、实验目的：

1.掌握离散时间信号和系统的频域分析方法；
2.学会利用MATLAB函数对离散时间信号和系统的频域进行计算。

二、实验原理：

1.离散时间傅里叶变换（DTFT）

	序列的离散时间傅里叶变换（DTFT）定义为：

通常是实变量Ω的复函数。实例程序演示如下：
【例3.1】求有限长序列的DTFT，并画出它的幅度谱，相位谱，实部和虚部。

clear all      -n<k<n
x=[1,2,3,4,5];
k=-1:3;
w=linspace(0,2*pi,512);
H=x*exp(-j*k'*w);
subplot(2,2,1);plot(w,abs(H));ylabel('幅度');     %画幅度特征曲线
subplot(2,2,2);plot(w,angle(H));ylabel('相角');   %画相位特征曲线
subplot(2,2,3);plot(w,real(H));ylabel('实部');    %画幅度实部特征曲线
subplot(2,2,4);plot(w,imag(H));ylabel('虚部');   %画幅度虚部特征曲线

其程序运行结果如下：

2.离散LTI系统的频率响应

利用MATLAB提供的freqz函数可以计算离散信号的频谱或离散系统频率响应的抽样值。
若信号的频谱表示为的有理多项式，则freqz函数其调用格式为：
X=freqz(b,a,w)

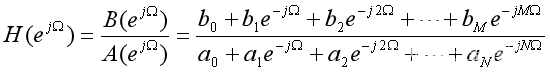
其中，X为系统频谱，w是抽样的频率点，b和a分别为离散LTI系统的系统函数的H(z)的分子和分母多项式系数。
说明：不带输入向量时freqz函数将自动绘出频率响应的幅频和相频特性曲线。

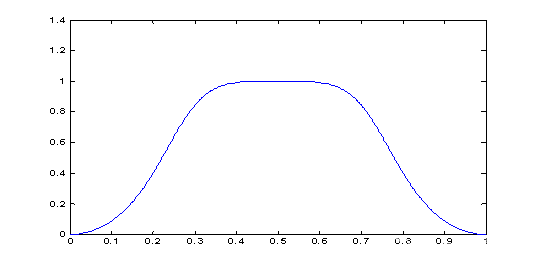
【例3.2】已知离散系统的H（z）为：

试画出该系统的幅度响应。
程序如下：

clear all
b1=[0.5009 -1.0019 0.5009];
b2=[0.5320 1.0640 0.5320];
a1=[1 -0.8519 0.4167];
a2=[1 0.8519 0.4167];
b=conv(b1,b2);  %计算H（z）的分子多项式系数
a=conv(a1,a2);  %计算H（z）的分母多项式系数
w=linspace(0,pi,512);
h=freqz(b,a,w);	
plot(w/pi,abs(h));

运行结果：

3.对X(z)部分分式展开

MATLAB提供了计算序列z变换X(z)的部分分式展开函数，其调用格式为：

[r,p,k]=residuez(b,a) 

其中， b和a分别为用表示X(z)的分子和分母多项式的系数。 若 X(z)的部分分式展开为：

则residuez的返回参数r,p,k分别为

residuez也可以用于由 r,p,k计算 表示X(z)的分子和分母多项式的系数，其调用格式为：

 [b,a]=residuez(r,p,k) 

4. X(z)的零极点函数

函数zplane可以画出X（z）的零极点坐标图，其调用格式是：

zplane(b,a)

[例3.3]试用MATLAB计算

的部分分式展开。并画出X（z）的零极点图。
程序如下：

clear all
b=[1.5,0.98,-2.608,1.2,-0.144];
a=[1,-1.4,0.6,-0.072];
[r,p,k]=residuez(b,a);
disp('留数');disp(r');
disp('极点');disp(p');
disp('常数');disp(k);
zplane(b,a);

程序的运行结果为：

留数
    0.7000    0.5000    0.3000
极点
    0.6000    0.6000    0.2000
常数
02

三、作业：

1.已知序列

画出该序列DTFT的实部、虚部、幅度谱和相位谱。并分析的特点。
程序如下：

clear all
N=pi
k=-pi:pi;
x=cos(pi*k/(2*pi));
w=linspace(-N,N);
H=x*exp(-j*k'*w);
subplot(2,2,1);plot(w,abs(H));ylabel('幅度');     %画幅度特征曲线
subplot(2,2,2);plot(w,angle(H));ylabel('相角');   %画相位特征曲线
subplot(2,2,3);plot(w,real(H));ylabel('实部');    %画幅度实部特征曲线
subplot(2,2,4);plot(w,imag(H));ylabel('虚部');   %画幅度虚部特征曲线

2.利用MATLAB函数计算的部分分式展开的各子系统的分子、分母多项式的系数。根据计算结果写出表达式.

程序如下：

clear all
b=[3,-7,-3,18];
a=[1,-5,6];
[r,p,k]=residuez(b,a);
disp('留数');disp(r');
disp('极点');disp(p');
disp('常数');disp(k);
zplane(b,a);

留数
    3.0000   -2.0000

极点
    3.0000    2.0000

常数
    2.0000    3.0000

表达式：

3.离散稳定的LTI系统的差分方程为
，画出该系统的频率响应函数，幅度谱，相位谱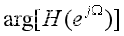及其零极点图。

程序如下：

clear all
b=[1];	
a=[1,-10/3,1];
w=linspace(-pi,pi,512);
[r,p,k]=residuez(b,a);
disp('留数');disp(r');
disp('极点');disp(p');
disp('常数');disp(k);
zplane(b,a);%零极点图
h=freqz(b,a,w);	
figure(2)
subplot(1,2,1);plot(w/pi,abs(h));ylabel('幅度');     %画幅度谱
subplot(1,2,2);plot(w/pi,angle(h));ylabel('相位');   %画相位谱
figure(3)
freqz(b,a,w)%频率响应函数