笔记分享: 西安交通大学COMP551705数据仓库与数据挖掘——06. 自然语言理解

有关 $\text{Github}$仓库，欢迎来 $\text{Star}$

$\text{1. NLU}$的概念与背景

1️⃣$\text{NLU}$与$\text{NLP}$

1. 自然语言理解：
   • 含义：让计算机理解人类语言的结构$+$语义
   • 应用：信息检索/情感识别/机器翻译/拼写检查/知识图谱构建
2. 自然语言处理：对自然语言的分析/理解/生成，即$\text{NLU+NLG(Generation)}$

2️⃣$\text{AI-Hard}$问题

1. 含义：问题等同于$\text{AI}$核心的问题，即如何让计算机具有人类智能
2. 典型：$\text{NLU/NLP}$，$\text{CV}$

3️⃣$\text{NLU}$面临的挑战

1. 计算机的特性：善于处理明确/结构化/无歧义的语言(如编程语言)
2. 自然语言特性：具有复杂的上下文以及歧义性($\text{Ambiguity}$)

   歧义类型	含义	示例
   词汇歧义	词汇具有不同含义	$\text{Fuck}$可以是动词/语气词
   句法歧义	一个句子被解析成不同的结构	南京市长江大桥
   语义歧义	句中包含了不明确的词	$\text{John kissed his wife, and so did Sam}$
   回指歧义	之前提到的词，在后面句子含义不同	小李告诉小王他生了
   语用歧义	短语/句子不同语境下含义不同	可以站起来吗 (询问能力$\text{or}$请求)

$\text{2. NLU}$的主要任务

$\text{2.1. NLU}$的语法任务

$\text{2.1.1. }$词汇层面的任务

1️⃣词干抽取($\text{Stemming}$)

1. 含义：抽取词的词干($\text{Stem}$)与词根($\text{root}$)，比如$\text{Niubilitiness}\to \{\begin{array}{l}\text{词干: Niubility}\\ \\ 词根\text{: Niubi}\end{array}$
2. 处理方法：

   方法	含义	限制
   利用形态规则	机械地去处所有后缀，如$\text{-ing/-tion}$	不规则变形词不适用
   基于词典	按照词典中的映射还原词性	受限于词典规模
   高级方法	$\text{n-gram}$法/隐马可夫/机器学习	受限于语料库大小

2️⃣词形还原($\text{Lemmatization}$)

1. 含义：将不同形式词汇还原为词目($\text{Lemma}$)，如$\text{am, is, are, was, were→be}$
2. 对比：词干抽取完全不考虑上下文，词形还原考虑一定的上下文
   • 示例：$\text{We are meeting in the zoom meeting}\underset{词形还原}{\overset{词干抽取}{\to }}\{\begin{array}{l}\text{词干抽取: meet}\\ \\ \text{词形还原: meet+meeting}\end{array}$
3. 处理方法：
   • 基于规则：人工给予的语言学规则，或者机器学习训练出来的规则
   • 基于词典：受限于词典，只适用于简单语言
     💡词形还原/词干抽取并非$\text{100\%}$必要，比如细颗粒度情感分析就需要高精度文本(时态/复数等)

3️⃣词性标注($\text{Part-of-speech tagging}$)

1. 含义：为文本中每个词标记词性(名词/动词/形容词)
2. 方法：基于规则(人工)，基于隐马可夫模型($\text{HMM}$)，基于机器学习(SVM/神经网络)
3. 挑战：分词$\text{\&}$词义多义性

4️⃣术语抽取($\text{Terminology extraction}$)

1. 含义：信息抽取的子任务，识别文本中特定领域的专门术语
2. 方法：机器学习，统计($\text{TF/IDF}$)，外部知识库
3. 挑战：新术语/跨领域术语

$\text{2.1.2. }$句法层面的任务

1️⃣句法分析($\text{Parsing}$)

1. 含义：分析文本中单词/短语之间的句法关系
   
2. 方法：统计学(概率上下文无关文法/最大化信息熵的原则)，机器学习方法($\text{RNN}$)

2️⃣断句($\text{Sentence breaking}$)

1. 含义：句子边界消歧(例如$\text{ . }$可表示短句/缩写/小数点等)$+$句子分割
2. 方法：基于最大熵，神经网络

3️⃣分词($\text{Word segmentation}$)

1. 含义：仅对词汇间没有明显边界的语言/中文而言，将连续字符分割为有意义单词
   
2. 方法：基于字典(正逆向匹配)，基于统计($\text{HMM/SVM}$)
3. 难处：未登录词/切分歧义

$\text{2.2. NLU}$的语义任务

$\text{2.2.1. }$文本生成/转换

1️⃣机器翻译

1. 含义：将文本/语音从一种语言翻译到另一种语言
2. 方法：基于规则(源/目标语言形态语法等)，基于统计(用大型语料库构建概率模型)，神经网络
3. 难题：词句歧义/对语料库大小强依赖/低频词句/长句子

2️⃣问答与对话

1. 含义：实现自然语言形式的人机交互
2. 分类：
   • $\text{5W1H}$类问题：即$\text{Who/What/When/Where/Why \& How}$
   • $\text{Open/Closed-domain}$类：回答可以没有限制 $\text{or}$ 专注于某一领域
3. 方法：检索法(从库中抽取语料回答)，生成法(检索$+$推理)，$\text{Pipeline}$，$\text{Seq2Seq}$
4. 难题：多知识约束/多轮对话/多模态/可解释性…

3️⃣自动文摘

1. 含义：为文档生成一段包含原文档要点的压缩文档，例如搜索引擎结果
   
2. 方法：对要点进行不修改的抽取，对要点概括(修改/复述)
3. 难题：难以评估，可理解性问题，需要背景知识

$\text{2.2.2. }$文本信息提取

1️⃣命名实体识别($\text{NER, Named entity recognition}$)

1. 命名实体：现实世界中的某个对象，如$\text{Obama is the president of the United States}$
2. $\text{NER}$：信息提取的子任务，识别文本中所有实体$+$分配到特定类别(名字/时间/数量)
3. 方法：语法规则(效果好但需要大量人工规则)，统计方法(需要标注大量数据)
4. 难题：领域依赖性(如医学实体/术语)，实体类型多样

2️⃣关系抽取

1. 含义：检测文本中实体的语义关系，并将各种关系分类
2. 方法：结合了领域知识的机器学习
3. 难点：训练集难以构建，自然语言的歧义

$\text{2.2.3. }$文本内容分析

1️⃣文本分类

1. 含义：自动将文本划分到预定类中，比如垃圾邮件过滤/情感识别/黄色内容识别
2. 方法：特征提取$\to$训练分类器(朴素贝叶斯/$\text{KNN}$/$\text{SVM}$)
3. 难题：特征难提取(需要大量标注)，数据非平衡问题

2️⃣情感分析

1. 含义：识别文本中的情感状态，主观评价等
2. 方法：情感词库($\text{Happy/Fucking}$)，统计方法($\text{SVM/}$潜在语义分析)
3. 难题：修辞的多样(反语/讽刺)，分面观点(即将复杂事物分解为不同方面)

3️⃣主题分割

1. 含义：将单个长文本分为多个较短的，主题一致的片段
2. 方法：
   • 基于内容变化：同一主题内容有高度相似性$\to$通过聚类
   • 基于边界特性：主题切换时会有边界(如过渡性/总结性文本)
3. 难点：任务目标模糊(主题多样)，无关信息干扰，歧义性

$\text{2.2.4. }$文本歧义消解

1️⃣词义消歧

1. 含义：确定一词多义词的含义
2. 方法：基于词典(叙词表/词汇知识库)，基于机器学习(小语料库的半监督学习/标注后的监督学习)
3. 难题：词义的离散型(一个词的不同含义可能完全不搭边)，需要常识

2️⃣共指消解

1. 含义：识别文本中表示同一个事物的不同代称
2. 示例：甲队打败了乙队，他们更强$\stackrel{消解后}{\to }$虽然甲队打败了乙队，但他们更强
3. 方法：
   • 启发式：如最接近语法兼容词，即在代词前寻找最近的$+$语法匹配的词
   • 基于$\text{ML}$：如$\text{Mention-Pair Models / Mention-Ranking Models}$
4. 难题：如何应用背景知识，歧义(哪哪都有它，考试的万金油解答嘿嘿)

$\text{3. }$自然语言的统计特性

$\text{3.1. Zipf}$定律

1️⃣$\text{Zipf}$定律

1. 内容：令出现频率第$r$高的词汇出现频率为$f(r)$，则有$f(r)\text{=}\frac{\text{Const}}{r^s}$其中$s\text{≈}1$
2. 含义：对于词频分布，最常见词的分布极为普遍$+$大多数词出现频率极低
3. 解释：

   解释模型	含义
   米勒猴实验	胡乱生成的带有字母$+$空格的序列，词频和排名也符合幂律关系
   最小努力原则	通过词频差异最小化交流的成本
   优先连接机制	网络结构中，新节点倾向于连接度数更大的点，与$\text{Zipf}$类似

2️⃣$\text{Zipf}$定律的实验

1. 符合程度：$f(r)\text{=}\frac{\text{Const}}{r^s}\to \log f(r)\text{=}\log C-s\log r$故可通过检测后者线性程度
2. 实验结论：幂律分布很常见$+$排名靠中间的术语会更符合
   

3️⃣$\text{Zipf}$定律与索引

0. 倒排索引：用于快速全文检索的数据结构，示例如下
   • 文档

     Doc1: fat cat rat rat 
     Doc2: fat cat 
     Doc3: fat
     

   • 构建的倒排索引

     fat: Doc1 Doc2 Doc3
     cat: Doc1 Doc2
     rat: Doc1
     

1. 词频太高/太低的词都不适合索引，会导致返回太多/太少的文档，适中的才最有价值
   
2. 基于$\text{Zipf}$定律，去处高频$\text{Stopword}$能优化倒排索引时空开销，如下为倒排索引的一个实例

$\text{3.2. Heaps}$定律

1️⃣$\text{Heaps}$定律

1. 内容：词汇表大小$V$与文本词数$n$满足$V\text{=}K{n}^{\beta }$
2. 参数：$10\text{≤}K\text{≤}100$且$0.4\text{≤}\beta \text{≤}0.6$，当$K\text{=}44$与$\beta \text{=}0.49$最匹配

2️⃣用途：预测随文本增长词汇表$\&$倒排索引大小的变化

$\text{3.3. Benford}$定律(第一数字法则)

1️⃣$\text{Benford}$定律

1. 背景：在许多社会现象中，数据首位数往往分布不均(为$1$概率最大$\stackrel{依次递减}{\to }$为$9$概率最小)
2. 定律：令数据集中$d$作为首字母的概率$P(d)=\lg \left(1+\frac{1}{d}\right)$，$d\text{＞}9$及非十进制时依旧适用

2️⃣对$\text{Benford}$定律的一些思考

1. 适用：跨数量级变化的数据集，如财务数据和自然现象
2. 应用：检测数据造假、异常值、验证财务报告真实性
3. 成因：还不具备完全的可解释性，大概是因为数据在对数尺的分布

$\text{4.}$ 词袋语言模型

$\text{4.1. BoW}$模型

1️⃣基本步骤：以句$\text{I love machine learning}$以及$\text{Machine learning is fun}$为例

步骤	示例
分词	$\text{I love machine learning }\text{Machine learning is fun}$
建表	$V\text{=[I, love, machine,lerning, is, fun]}$
向量化	第一句变为$A_1\text{=[1,1,1,1,0,0]}$第二局变为$A_2\text{=[0,0,1,1,1,1]}$

2️⃣特点

1. 原理上：完全忽略了语法/词序，默认词与词间的概率分布独立
2. 效果上：
   • 优点：实现极其简单，但高效且应用广泛
   • 缺点：无法区分$\text{\&}$一义多词，如同义词替换后的两文档相似度低于实际值

$\text{4.2. TF-IDF}$模型

1️⃣$\text{TF-IDF}$值

1. 计算: $\text{TF-IDF}(t,d)\text{=TF}(t,d)\text{×IDF(}t)\text{→}\{\begin{array}{l}词频\text{TF}(t,d)=\frac{词t在文档d出现次数}{文档d总词数}\\ \\ 逆文档频\text{IDF(t)=}\log \frac{文档总数}{\text{DF}(t)(包含t的文档数)\text{+}1}\end{array}$
2. 含义: $\text{TF-IDF}(t,d)$越高，代表词$t$对文档$d$越重要

2️⃣$\text{TF-IDF}$值改进：原始词频值往往不是所需的

1. 对原始词频$\text{TF}(t,d)$的改进

   词频类型	公式	意义
   对数	$1\text{+}\log (\text{TF}(t,d))$	压缩较高词频，减少其对相关性影响的夸大
   增强	$0.5\text{+}\frac{0.5\text{×}\text{TF}(t,d)}{{\max }_{\mathrm{t}}\text{TF}(t,d)}$	映射词频到$0.5\text{→1}$，防止高频词权重过大
   布尔	$\{\begin{array}{l}1\text{ if }\text{TF}(t,d)>0\\ 0\text{ otherwise }\end{array}$	不关注具体的词频值，仅表示是否出现
   平均对数	$\frac{1+\log \left(\text{TF}(t,d)\right)}{1+\log \left({\mathrm{ave}}_{\mathrm{t}\in \mathrm{d}},\left(\text{TF}(t,d)\right)\right)}$	使词频高的词与低的词之间的差距不会过大

2. 对文档频率$\text{DF}(t)$的改进：$N$是文档总数

   文档频率$\text{DF}(t)$	公式	意义
   逆文档频率$\text{IDF}(t)$	即$\log \frac{N}{\text{DF}(t)}$者$\log \frac{N}{\text{DF}(t)\text{+1}}$	衡量词在文档集合中的稀有性
   概率文档频率$\text{ProbDF(}t)$	$\max \left\{0,\log \frac{N-\text{DF}(t)}{\text{DF}(t)}\right\}$	通过概率角度评估词的稀有性

3. 归一化：对于$\text{TF-IDF}\text{=}\left[\begin{array}{cccc}\text{TF-IDF}(t_1,d_1)& \text{TF-IDF}(t_1,d_2)& \cdots & \text{TF-IDF}(t_1,d_n)\\ \text{TF-IDF}(t_2,d_1)& \text{TF-IDF}(t_2,d_2)& \cdots & \text{TF-IDF}(t_2,d_n)\\ ⋮& ⋮& \ddots & ⋮\\ \text{TF-IDF}(t_m,d_1)& \text{TF-IDF}(t_m,d_2)& \cdots & \text{TF-IDF}(t_m,d_n)\end{array}\right]$

   归一类型	公式	意义
   余弦归一	$\text{TF-IDF}\text{×}\frac{1}{\sqrt{\sum _{i=1}^m\sum _{j=1}^n[\text{TF-IDF}(t_i,d_j){]}^2}}$	用于计算文档间的余弦相似度
   基准归一	$\text{TF-IDF}\text{×}\frac{1}{mn}$	消除文档集合大小对权重的影响
   字长归一	$\text{TF-IDF}\text{×}\frac{1}{{\text{(CharLen)}}^{\alpha }}$	适用于不同长度的文档，且$\alpha \text{<}1$

3️⃣基于$\text{TF-IDF}$的余弦相似度

1. $\text{TF-IDF}$值：对于文档$d_1$和$d_2$，词汇表长为$m$
   • $\text{TF-IDF}\text{=}\left[\begin{array}{cc}\text{TF-IDF}(t_1,d_1)& \text{TF-IDF}(t_1,d_2)\\ \text{TF-IDF}(t_2,d_1)& \text{TF-IDF}(t_2,d_2)\\ ⋮& ⋮\\ \text{TF-IDF}(t_m,d_1)& \text{TF-IDF}(t_m,d_2)\end{array}\right]\stackrel{余弦归一化}{\to }\left[\begin{array}{cc}\text{tf-idf}(t_1,d_1)& \text{tf-idf}(t_1,d_2)\\ \text{tf-idf}(t_2,d_1)& \text{tf-idf}(t_2,d_2)\\ ⋮& ⋮\\ \text{tf-idf}(t_m,d_1)& \text{tf-idf}(t_m,d_2)\end{array}\right]$
2. 两文档余弦值：
   • 未归一化表示：$\text{sim}(d_1,d_2)=\frac{\sum _{j=1}^m\text{TF-IDF}(t_j,d_1)\cdot \text{TF-IDF}(t_j,d_2)}{\sqrt{\sum _{j=1}^m(\text{TF-IDF}(t_j,d_1){)}^2}\cdot \sqrt{\sum _{j=1}^m(\text{TF-IDF}(t_j,d_2){)}^2}}$
   • 归一化表示 ：$\text{sim}(d_1,d_2)=\sum _{j=1}^m\text{tf-idf}(t_j,d_1)\cdot \text{tf-idf}(t_j,d_2)$

$\text{5 }$主题语言模型

$\text{5.0. }$概述

1️⃣分布模型：$\text{Doc.}\underset{非监督学习(聚类)}{\overset{主题分布}{\to }}\{\begin{array}{l}\text{Topic 1}(P_{T_1})\underset{非监督学习(聚类)}{\overset{词语分布}{\to }}\{\begin{array}{l}{\text{Word}}_{11}(P_{W_{11}})\\ {\text{Word}}_{12}(P_{W_{11}})\\ ⋮\\ {\text{Word}}_{1m}(P_{W_{1m}})\end{array}\\ \text{Topic 2}(P_{T_2})\underset{非监督学习(聚类)}{\overset{词语分布}{\to }}\{\begin{array}{l}{\text{Word}}_{21}(P_{W_{21}})\\ {\text{Word}}_{22}(P_{W_{21}})\\ ⋮\\ {\text{Word}}_{2m}(P_{W_{2m}})\end{array}\\ ⋮\\ \text{Topic n}(P_{T_n})\underset{非监督学习(聚类)}{\overset{词语分布}{\to }}\{\begin{array}{l}{\text{Word}}_{n1}(P_{W_{n1}})\\ {\text{Word}}_{n2}(P_{W_{n1}})\\ ⋮\\ {\text{Word}}_{nm}(P_{W_{nm}})\end{array}\end{array}$

1. 主题分布：每篇文档由若干主题按一定比例构成
2. 词语分布：每个主题包含一组特定的词语，每个词具有不同的出现概率

2️⃣概率模型

1. 公式：$p(w|\mathrm{Doc})=\sum _{i=1}^{n}p\left(w|T_i\right)\cdot p\left(T_i|\mathrm{Doc}\right)$
2. 含义：将文档的内容视为不同主题的组合$\to$由每主题的词语概率预测文档中词语的分布

$\text{5.1. }$基于矩阵分解的模型

$\text{5.1.1. LSA(SVD)}$模型

1️⃣奇异值分解

1. 含义：对任意$A_{m\text{×}n}$可将其分解为三个矩阵$A_{m\text{×}n}\text{=}{U}_{m\text{×}m}{\Sigma }_{m\text{×}n}{V}_{n\text{×}n}^T$

   矩阵类型	描述
   左奇异矩阵$U_{m\text{×}m}$	为正交矩阵即$U_{m\text{×}m}{U}_{m\text{×}m}^T\text{=}{I}_{m\text{×}m}$
   奇异值矩阵${\Sigma }_{m\text{×}n}$	为对角矩阵(对角为是奇异值)，如${\left[\begin{array}{ccccccc}{\alpha }_1& 0& 0& \cdots & 0& \cdots & 0\\ 0& {\alpha }_2& 0& \cdots & 0& \cdots & 0\\ 0& 0& {\alpha }_3& \cdots & 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& & ⋮\\ 0& 0& 0& \cdots & {\alpha }_m& \cdots & 0\end{array}\right]}_{m\text{×}n}$
   右奇异矩阵$V_{n\text{×}n}$	为正交矩阵即$V_{n\text{×}n}{V}_{n\text{×}n}^T\text{=}{I}_{n\text{×}n}$

2. $\text{Eckart–Young–Mirsky}$定理：$A_k=U_k{\Sigma }_k{V}_k^T$奇异值的截断
   • $U_k$ 和 $V_k$ 分别是 $U$ 和 $V$ 的前 $k$ 列
   • ${\Sigma }_k$ 是奇异值矩阵 $\Sigma$ 中前 $k$ 个最大的奇异值组成的 $k\text{×}k$ 子矩阵

2️⃣$\text{LSA}$模型步骤：原始$\text{Word-Doc}$矩阵$\underset{近似}{\overset{奇异分解}{\to }}$其近似的低阶矩阵

1. $\text{Word-Doc}$矩阵：
   • $A_{t\text{×}d}=\left[\begin{array}{cccc}{\text{Doc}}_1\text{→}{\text{Word}}_{11}& {\text{Doc}}_2\text{→}{\text{Word}}_{12}& \cdots & {\text{Doc}}_n\text{→}{\text{Word}}_{1d}\\ {\text{Doc}}_1\text{→}{\text{Word}}_{21}& {\text{Doc}}_2\text{→}{\text{Word}}_{22}& \cdots & {\text{Doc}}_n\text{→}{\text{Word}}_{2d}\\ ⋮& ⋮& \ddots & ⋮\\ {\text{Doc}}_1\text{→}{\text{Word}}_{t1}& {\text{Doc}}_2\text{→}{\text{Word}}_{t2}& \cdots & {\text{Doc}}_n\text{→}{\text{Word}}_{td}\end{array}\right]$
   • ${\text{Doc}}_i{\text{→Word}}_{ij}$可为词${\text{Word}}_{ij}$的词频或者$\text{TF-IDF}$值
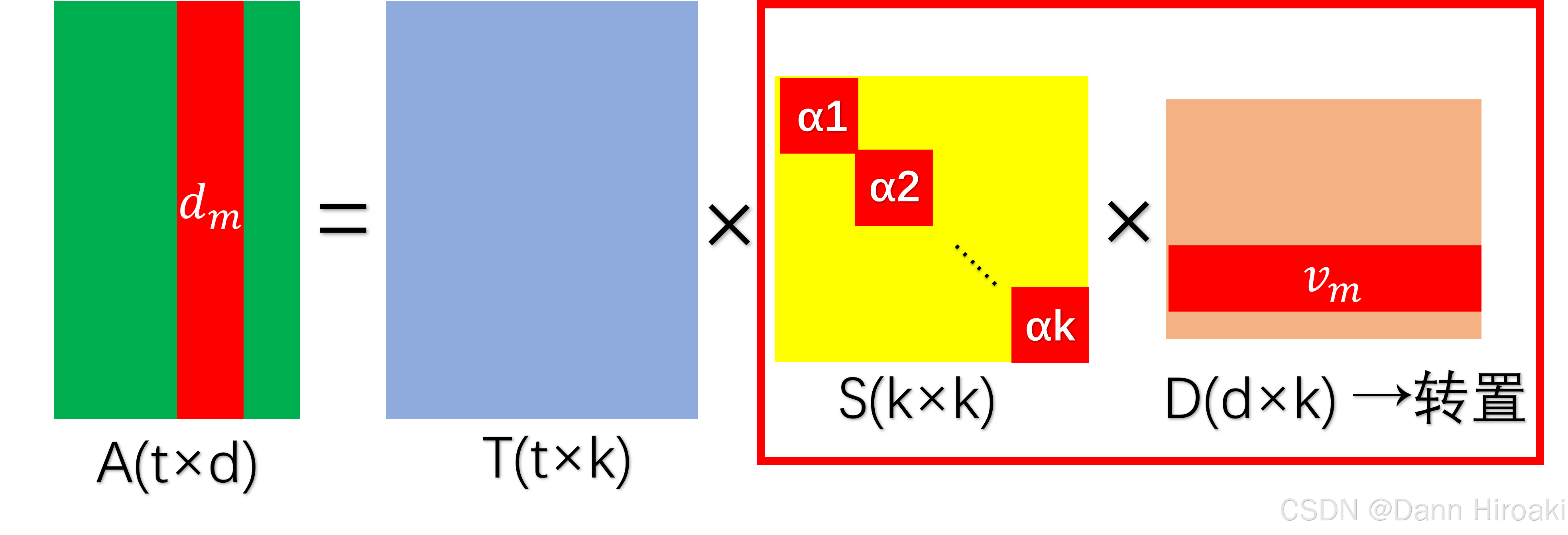
2. $A_{t\text{×}d}$奇异分解：$A_{t\text{×}d}\text{=}{T}_{t\text{×}n}{S}_{n\text{×}n}{D}_{d\text{×}n}^T$
   

   矩阵类型	描述
   $S_{n\text{×}n}$	奇异值按降序排列，代表重要的潜在语义的强度
   $T_{t\text{×}n}$	词汇矩阵，每列蕴含一个隐含概念(主题)
   $D_{d\text{×}n}$	文档矩阵，每列蕴含一个隐含概念(主题)

3. 低秩近似： $A\text{→}{A}_k$
   
   • 降维： $S_{n\text{×}n}\stackrel{只保留前k个最大的奇异值}{\to }{S}_{k\text{×}k}$，其中$k$又称为预期主题数
   • 降噪：$A_{t\text{×}d}\text{=}{T}_{t\text{×}n}{S}_{n\text{×}n}{D}_{d\text{×}n}^T\stackrel{S_{n\text{×}n}降维}{\to }{A}_{t\text{×}d}\text{=}{T}_{t\text{×}k}{S}_{k\text{×}k}{D}_{d\text{×}k}^T$，滤掉不重要的主题

3️⃣文档与词汇的表示

1. 词汇：$T_{t\text{×}k}{S}_{k\text{×}k}$的行向量，且${\hat{w}}_n=u_n\text{×}\text{S}$
   
2. 文档：$D_{d\text{×}k}{S}_{k\text{×}k}$的行向量($S_{k\text{×}k}{D}_{d\text{×}k}^T$的列向量)，且${\hat{d}}_m\text{=}\text{S}\text{×}{v}_m^T$
   

$\text{5.1.2. MNF}$建模

1️⃣建模过程

1. 对$\text{V}$寻找非负矩阵$\text{HW}$使$\text{V}\text{≈}\text{WH}$
2. 使得代价函数$\Vert V-WH\Vert \text{=}\sqrt{\sum _{i,j}{\left(V_{i,j}-(WH{)}_{i,j}\right)}^2}$ 尽可能小

2️⃣建模的意义

1. 非负：使分解结果更有意义
2. 示例：文档-单词$\stackrel{\text{NMF}}{\to }$文档-主题$\text{×}$主题-单词

$\text{5.2. }$基于概率的模型

$\text{5.2.0. }$概率模型概述

1️⃣符号：其中$K$为话题数，$K\text{≪}M$且为预先定义的超参数

集合	含义	随机变量
文本集 D = { d 1 , d 2 , . . . d N } D\text{=}\{d_1,d_2,...d_N\} D={d1​,d2​,...dN​}	包含所有文本，$N$为文本总数	$d$(观测变量)
话题集 Z = { z 1 , z 2 , . . . z K } Z\text{=}\{z_1,z_2,...z_K\} Z={z1​,z2​,...zK​}	包含所有可能的话题，$K$为预设话题总数	$z$(隐藏变量)
词汇集 W = { w 1 , w 2 , . . . w M } W\text{=}\{w_1,w_2,...w_M\} W={w1​,w2​,...wM​}	所有可能的单词，$M$为单词总数	$w$(观测变量)

2️⃣三类分布：$P(d)$为可观测参数，如何估计$P(z|d)$和$P(w|z)$两参数派生了$\text{pLAS}$和$\text{LDA}$方法

分布	表示	含义
文档分布	$P(d)\sim$多项分布	生成文本$d$的概率
主题分布	$P(z\mid d)\sim$多项分布	文本$d$生成话题$z$的概率，每个文本都有其主题分布
单词分布	$P(w\mid z)\sim$多项分布	话题$z$生成单词$w$的概率，每个主题都有其单词分布

3️⃣观测表征

1. 观测数据：文本-单词共现矩阵，其中$n($单词$i,$ 文本$j)$表示单词$i$在文本$j$中出现的次数

   共现矩阵$T$	文$d_1$	文$d_2$	$\text{...}$	文$d_N$
   词$w_1$	$n($词$w_1,$ 文$d_1)$	$n($词$w_1,$ 文$d_2)$	$\text{...}$	$n($词$w_1,$ 文$d_N)$
   词$w_2$	$n($词$w_2,$ 文$d_1)$	$n($词$w_2,$ 文$d_2)$	$\text{...}$	$n($词$w_2,$ 文$d_N)$
   $\text{...}$	$\text{...}$	$\text{...}$	$\text{...}$
   词$w_M$	$n($词$w_M,$ 文$d_1)$	$n($词$w_M,$ 文$d_2)$	$\text{...}$	$n($词$w_M,$ 文$d_N)$

2. 生成概率：假设每个单词分布独立，则有$P(T)\text{=}\prod _{(w,d)}P(w,d{)}^{n(w,d)}$

4️⃣$\text{LDA}$与$\text{pLSA}$

模型	思想	对于两$P(z\mid d)$和$P(w\mid z)$待估参数
$\text{pLSA}$	频率学	视作固定值(即均匀分布)，用最大似然估计解出来
$\text{LDA}$	贝叶斯	视作服从$\text{Dirichlet}$分布的随机变量，先验分布$\stackrel{修正}{\to }$最终分布

$\text{5.2.1 pLSA}$模型

1️⃣生成模型：

1. 定义：对生成概率$P(w,d)\text{=}P(d)\sum _{z}P(z|d)P(w|z)$形式的拆解
2. 概率依赖：文本$\text{→}$话题$\text{→}$单词
   

   选择	描述	备注
   文本	从$D$中，按$P(d)$选择文本$d\stackrel{重复N次}{\to }$生成$N$个文本	$N$为文本数量
   话题	对每个文本，按$P(z\mid d)$选择话题$z\stackrel{重复L次}{\to }$生成$L$个话题	$L$为文本(定/变)长
   单词	对每个话题，按$P(w\mid z)$选择一单词	$\text{N/A}$

2️⃣共现模型：

1. 定义：对生成概率$P(w,d)\text{=}\sum _{z\text{∈}Z}P(z)P(w|z)P(d|z)$形式的拆解
2. 概率依赖：话题$\text{→}$单词，话题$\text{→}$文本
   

   选择	描述	备注
   话题	从$Z$中，按$P(z)$选择话题$z\stackrel{重复L次}{\to }$生成$L$个话题	$L$为文本(定/变)长
   单词	对每个话题，按$P(w\mid z)$选择一单词	单词/文本的选择独立
   文本	从$D$中，按$P(d\mid z)$选择文本$d\stackrel{重复N次}{\to }$生成$N$个文本	$N$为文本数量

$\text{5.2.2. LDA}$模型简述

💢别看$\text{PPT}$了那就是一坨屎，以下内容来自维基百科

1️⃣$\text{LDA}$模型要素

1. 三种分布：

   分布	维度	元素	隐藏/观测
   主题分布$\Theta$	文档数$\text{×}$主题数	${\theta }_{i,j}$为文档$i$中主题$j$的比例	隐藏
   词汇分布$\beta$	主题数$\text{×}$词汇数	${\beta }_{i,j}$为主题$i$中词汇$j$的频次	隐藏
   主题分布$\text{w}$	文档数$\text{×}$词汇数	${\text{w}}_{i,j}$为文档$i$中词汇$j$的频次	观测

2. 两种超参数：

   超参数	描述	功能
   $\alpha$	文档集级参数，$\text{Dirichlet}$分布参数	生成文档的主题$\Theta$
   $\eta$	文档集级参数，$\text{Dirichlet}$分布参数	生成每个主题的$\beta$

2️⃣$\text{LDA}$的生成：分布$p\left(w_i,z_i,{\theta }_i,\Phi \mid \alpha ,\beta \right)=\prod _{j=1}^{N}p\left({\theta }_i\mid \alpha \right)p\left(z_{i,j}\mid {\theta }_i\right)p(\Phi \mid \beta )p\left(w_{i,j}\mid {\varphi }_{z_{i,j}}\right)$

1. 第一部分：
   • 从先验$\text{Dirichlet}$分布$\alpha$中抽样$\text{→}$生成某一文档$i$的主题(多项式)分布${\theta }_i$
   • 从${\theta }_i$分布中抽样$\text{→}$生成某一文档$i$的某一主题$z_{i,j}$
2. 第二部分：
   • 从先验$\text{Dirichlet}$分布$\eta$中抽样$\text{→}$生成主题$z_{i,j}$的词语分布${\beta }_{z_{i,j}}$
   • 从${\beta }_{z_{i,j}}$分布中抽样$\text{→}$生成词语$w_{i,j}$

4️⃣$\text{LDA}$的求解(训练)：我也不信考试会考这$\text{B}$玩意儿

1. $\text{EM}$算法($\text{Old-Fashioned}$)
2. $\text{Gibbs}$采，$\text{MCMC(Markov Chain Monte Carlo)}$算法

$\text{5.2.3. }$番外: $\text{pLSA}$的$\text{EM}$求解

0️⃣总体思路

1. 极大似然估计：找到时$P(T)$最大的参数
2. $\text{EM}$算法：直接最大化对数似然函数非常困难，从而通过$\text{EM}$迭代的方式实现

1️⃣极大似然函数

1. 似然函数推导
   • 给定共现数据 T = { n ( w i , d j ) } → \textbf{T}=\{n(w_i,d_j)\}\text{→} T={n(wi​,dj​)}→要让$P(T)\text{=}\prod _{i,j}P(w_i,d_j{)}^{n(w_i,d_j)}$最大
   • 取对数$+$引入隐含变量：
     $$\begin{gathered} \begin{array}{rlr}& \log P(T)\text{=}\sum _{i=1}^M\sum _{j=1}^{N}n(w_i,d_j)\text{×}\log P(w_i,d_j)& \\ & \Downarrow \\ 引入隐含变量\text{: }p\left(d_j\right)\sum _{z}p\left(z_k|d_j\right)p\left(w_i|z_k\right) \\ & \\ & \log P(T)\text{=}\sum _{i=1}^M\sum _{j=1}^N\left(n(w_i,d_j)\text{×}\left(\log p(d_j)\text{+}\log \left(\sum _{z}p(z_k|d_j)p(w_i|z_k)\right)\right)\right)& \end{array} \end{gathered}$$
2. 似然函数分析：
   • 已知值：$n(w_i,d_j)$在$\text{T}$向量中就有之，$p(d_j)$可由真实大量文本集得到
   • 参数值：$\log \left(\sum _{z}p(z_k|d_j)p(w_i|z_k)\right)$，其中$\log \sum$形式适合用$\text{EM}$算法解决

2️⃣极大似然函数的下界

1. $\text{Jensen}$不等式

   情况	$E(f(x))$与$f(E(x))$
   $f(x)$为凸函数	$E(f(x))\ge f(E(x))$
   $f(x)$为凹函数	$E(f(x))\le f(E(x))$
   $x\text{=}C$	$E(f(x))=f(E(x))$

2. $\log \left(\sum _{z}p(z_k|d_j)p(w_i|z_k)\right)$的处理：构建方差$+$应用$\text{Jensen}$不等式
   • $\sum _{z}p(z_k|d_j)p(w_i|z_k)\stackrel{z的分布Q(z)}{\to }\sum _{z}Q(z)\frac{p(z_k|d_j)p(w_i|z_k)}{Q(z)}\stackrel{X\text{=}\frac{p(z_k|d_j)p(w_i|z_k)}{Q(z)}}{\to }E(X)$
   • 原式$\text{=}\log (E(X))\underset{\text{Jensen不等式}}{\overset{\log (x)为凹函数}{\to }}\text{≥}E(\log (X))\text{=}\sum _z\left(\log \frac{p(z_k|d_j)p(w_i|z_k)}{Q(z)}\right)Q(z)$
3. 下界与极大似然：提升下界$\sum _z\left(\log \frac{p(z_k|d_j)p(w_i|z_k)}{Q(z)}\right)Q(z)$的最大值$\text{→}$最大化似然函数

3️⃣$\text{EM}$算法：详细步骤就不写了，我不信考试会考这$\text{B}$玩意儿

1. $\text{E}$步：确定$Q$函数$\text{→}$表示当前参数估计下完全数据(观测数据$+$隐含变量)的对数似然的期望
   • 此处$Q\text{=}Q(z)\text{=}p(z_k|w_i,d_j)$
2. $\text{M}$步：迭代$Q$函数，不断更新参数$\to$使当前参数估计靠近最优值
   • 此处需要更新的参数为文档-主题分布$P(z|d)$，主题-词汇分布$P(w|z)$
   • 最终使$\sum _z\left(\log \frac{p(z_k|d_j)p(w_i|z_k)}{Q(z)}\right)Q(z)$最大，从而使$P(T)$最大