思路:
读完题之后深感懵逼
好!我们来分析一下 , 对于这个题我们要先有一个两条路线同时进行的思想。 PS: (注意这题不能用贪心去做, 常见的错误思路是 , 我们先进行第一次dp直接将从
(
1
,
1
)
(1,1)
(1,1) 到
(
n
,
n
)
(n , n)
(n,n) 的 第一次最大值算出来, 将这条路径上的数清零后再算第二条路径, 实际上这种是错误的, 第一次走为局部最优并且也对第二次走造成了影响,第二次走是在第一次影响下所能走的局部最优,不具备无后效性,因此分开两次走并不是全局最优解 ) , 所以我们要同时进行 用
(
i
1
,
j
1
)
,
(
i
2
,
j
2
)
(i1 , j1) , (i2,j2)
(i1,j1),(i2,j2) 表示两个点的位于的位置;
f
[
i
1
,
j
1
,
i
2
,
j
2
]
f[ i1, j1 , i2 , j2]
f[i1,j1,i2,j2] 表示当第一个人走到
[
i
1
,
j
1
]
[i1,j1]
[i1,j1] 并且第二个人走到
[
i
2
,
j
2
]
[i2,j2]
[i2,j2] 的时候两者的取得的数字和为最大, 很明显这是一个四维背包问题, 我们需要进行一个优化, 我们可以发现 由于只能往下和往右去走这个时候我们可以设一个未知数k去合并两个点的某些性质, 令 k 表示我们走到的点的坐标和即 k = i1 + j1 = i2 + j2 ; 注意即使i1 + j1 = i2 + j1 两点也不一定重合(更准确的说两点是在一个边长是k的子矩阵的副对角线上的任意两点 ) , 不难看出k的取值范围是
[
2
,
2
∗
n
]
[2, 2*n]
[2,2∗n] , 判断两点是否是同一点, 只需判断 i1 是否等于i2 即可。
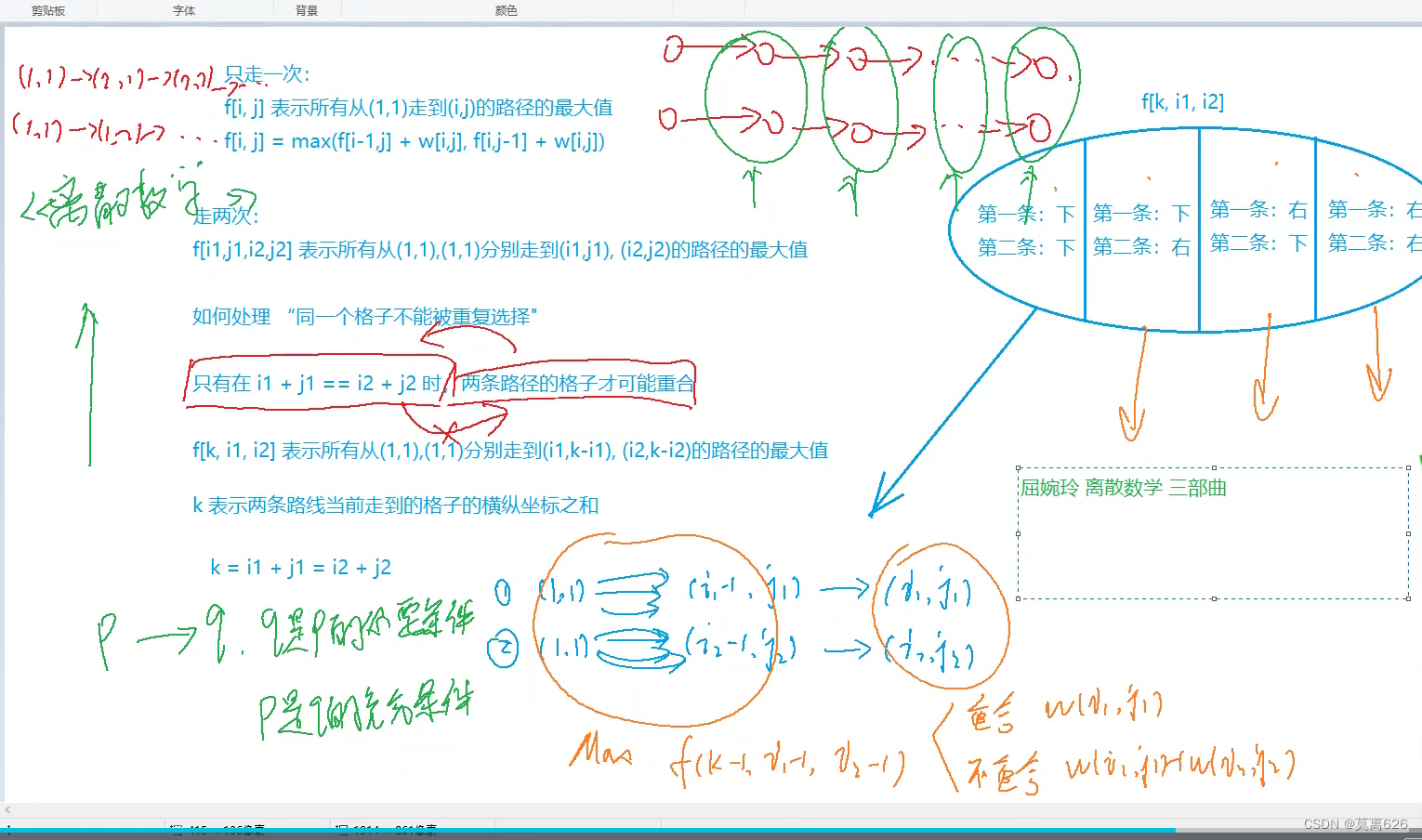
之后我们需要进行一个状态转移:
看图片右上角集合的划分!
#include <iostream>
using namespace std ;
const int N = 110 ;
int w[N][N] ;
int f[N*2][N][N] ;
int main()
{
int n , a , b , c ;
cin >> n ;
while(cin >> a >> b >> c , a || b || c) w[a][b] = c;
for(int k = 2 ; k <= n * n ; k ++ )
{
for(int i1 = 1 ; i1 <= n ; i1 ++ )
{
for(int i2 = 1; i2 <= n ; i2 ++ )
{
int j1 = k - i1 , j2 = k - i2 ;
if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n )
{
int t = w[i1][j1] ;
if(i1 != i2 ) t += w[i2][j2] ;
int &x = f[k][i1][i2] ;
x = max(x , f[k - 1][i1 - 1][i2 - 1] + t ) ;
x = max(x , f[k - 1][i1][i2 - 1] + t) ;
x = max(x , f[k - 1][i1 - 1][i2] + t ) ;
x = max(x , f[k -1 ][i1][i2] + t ) ;
}
}
}
}
printf("%d" , f[n *2][n][n] ) ;
return 0 ;
}
2.线性dp
题意
思路:对于这一道题实际上求的是最长的单峰子序列 , 所以我们可以这样想, 按照位置去划分状态, 分别以 1..... n 1 ..... n 1.....n 之间的任何一个数作为峰顶 , 按照这种思路直接做不好做, 如果最外层枚举峰顶的时候这时候我们的时间复杂度是 n 3 n^3 n3 的, 但如果我们先预处理出每一个位置的left数组和right数组就可以将时间复杂度控制在 n 2 n^2 n2 了。 left数组含义是 : l e f t [ i ] left[i] left[i] 以i结尾的最长上升子序列 , r i g h t [ i ] right[i] right[i] : 以i开头的最长下降子序列。 预处理之后再来一个线性的遍历, 用res 存储最大值即可, 注意最终的答案是 r e s − 1 res - 1 res−1 ;
AC代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010 ;
int n ;
int f[N] ;
int arr[N] ,l[N] , r[N] ;
int main()
{
cin >> n ;
for(int i = 1 ; i <= n ; i ++ ) cin >> arr[i] ;
for(int i = 1; i <= n ; i ++ )
{
l[i] = 1 ;
for(int j = 1; j < i ; j ++ )
{
if(arr[i] > arr[j] ) l[i] = max(l[i] , l[j] + 1) ;
}
}
for(int i = n ; i ; i -- )
{
r[i] = 1 ;
for(int j = n ; j > i ; j -- )
{
if(arr[i] > arr[j] ) r[i] = max(r[i] , r[j] + 1) ;
}
}
int res = 0 ;
for(int i = 1 ; i <= n ; i ++ )
{
res = max(res , l[i] + r[i] ) ;
}
cout << res - 1 << endl ;
return 0;
}
第三题
dp + 贪心
思路:第一问相当于求解的是 不上升组序列的最大长度, 这个没什么好说的 , 但对于第二问, 这个需要我们认真的思考一下, 对于第
i
i
i号导弹来说, 要么选择让前面的某一个导弹系统进行拦截, 要么再新开一个新的导弹系统去拦截 , 那么这个导弹能被前面的某一个导弹系统拦截的条件是什么?
我们需要看当先前面的导弹系统的最后一个拦截的导弹的高度(所以我们可以维护每一套导弹拦截系统的最后一个拦截的导弹的高度 ) , 如果第
i
i
i个导弹的拦截高度严格大于前面的任何一个导弹拦截系统的高度 ,这个时候我们就需要去再新创建一个导弹拦截系统 。
代码块
// g数组存储每一个导弹系统的最小的导弹拦截高度
int p = lower_bound(g, g+cnt, a[i]) - g;
if(p == cnt) g[cnt ++] = a[i]; //a[i]开创一套新拦截系统 , (代表a[i] 大于g数组内的所有元素)
else g[p] = a[i]; //a[i]成为第p套拦截系统最后一个导弹高度
还有一个 问题就是如果前面有多个导弹系统满足a[i] <= g[i] 我们该插入哪个里面呢?? ,(也就是对应的上面的代码块里面的else的部分) , 插入的应该是
>
=
a
[
i
]
>= a[i]
>=a[i] 的最小的
g
[
i
]
g[i]
g[i] 所对应的导弹拦截系统, ( 我们可以使用lower_bound() 函数去求 ) 这是一个贪心的证明:
见链接 这个大佬的证明 : 证明 orz
代码:
#include <iostream>
using namespace std;
const int N = 1010 ;
int f[N] ;
int arr[N] ;
int g[N] ; // 存储每一个导弹系统的最小的导弹拦截高度
int main()
{
int cnt = 0 , n = 0 ;
while(cin >> arr[n] ) n ++ ;
int res = 0 ;
for(int i = 0 ; i < n ; i ++ )
{
f[i] = 1 ;
for(int j = 0 ; j < i ; j ++ )
{
if(arr[j] >= arr[i] ) f[i] = max(f[i] , f[j] + 1) ;
}
res = max(res , f[i] ) ;
int p = lower_bound(g , g + cnt , arr[i] ) - g ;
if(p == cnt ) g[cnt++] = arr[i] ;
else g[p] = arr[i] ;
}
cout << res << endl ;
cout << cnt << endl ;
return 0 ;
}
---------------------------------------------------------------------------------------------
分割线
思路:这是一道经典dp问题; 我们将每一个数用二进制表示, 我们可令f[i] 表示在集合中的数字的二进制有效长度是 i i i的 个数 所以 f [ 1 ] = 1 f[1] = 1 f[1]=1 , 我们可以发现的是, 对于 f [ i ] f[i] f[i] 来说, f [ i ] = f [ i − 1 ] + f [ i − 2 ] f[i] = f[i - 1] + f[i-2] f[i]=f[i−1]+f[i−2] , 这个是每个长度下的个数 , 之后我们再求出一个简单的前缀和就行了。
AC代码:
#include <iostream>
using namespace std;
const int N = 1e6 + 10 , mod = 998244353 ;
int f[N] ;
int main()
{
int p ;
cin >> p ;
f[1] = 1;
for(int i = 2 ; i <= N ; i ++)
{
f[i] = f[i - 1] + f[i - 2] ;
f[i] = f[i] % mod ;
}
int sum = 0 ;
for(int i = 1 ; i <= p ; i ++ )
{
sum = (sum + f[i]) % mod ;
}
cout << sum << endl ;
return 0;
}
多重背包二进制优化技巧
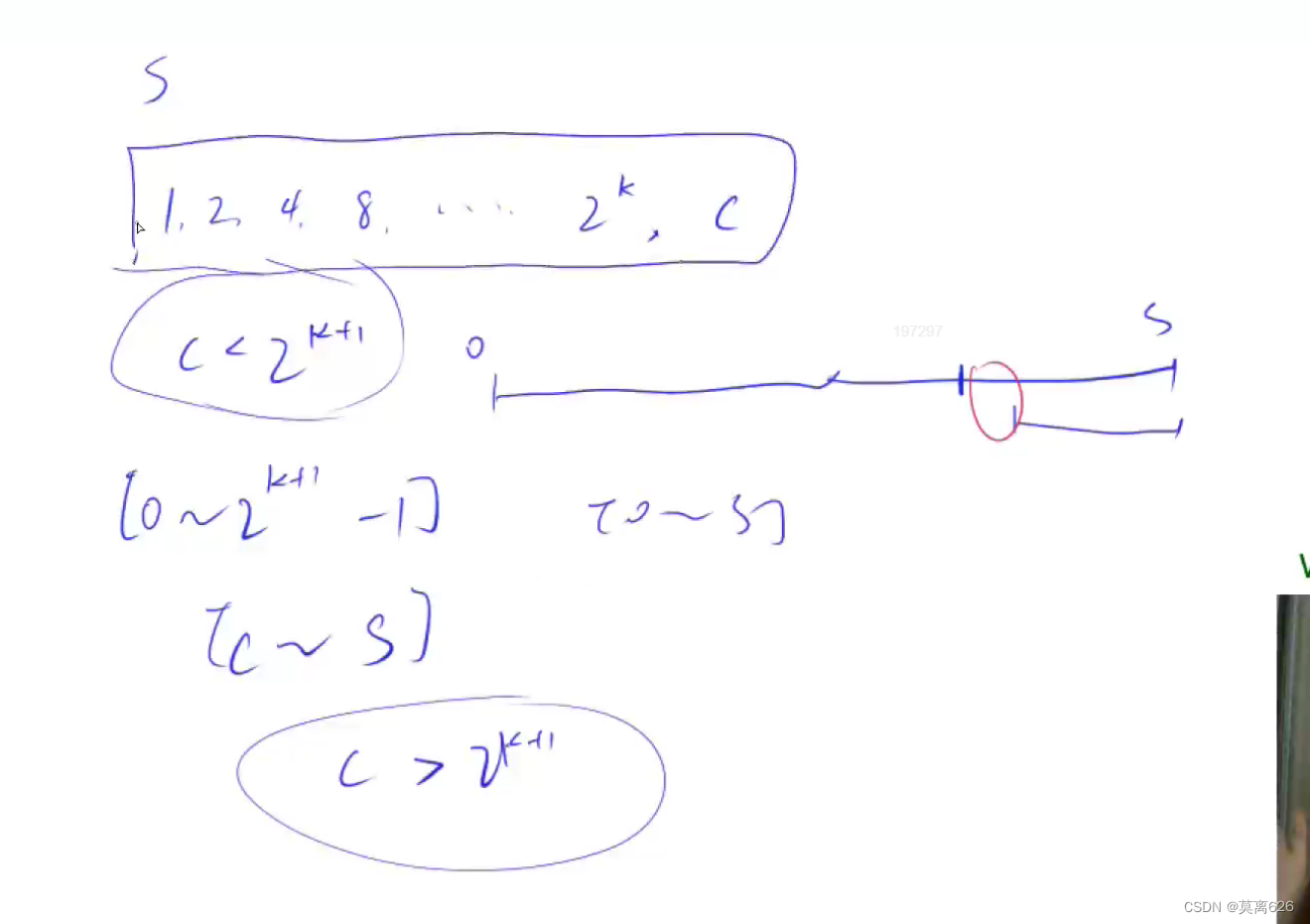
例如一个正整数 s 我们如何用最少的几个数根据是否选择去只能表示0 ~ s 之内的所有数呢? 这个可以使用二进制优化的思想, 答案的个数就是
l
o
g
s
logs
logs 向上取整, 解释:
(直接上图):

状态压缩
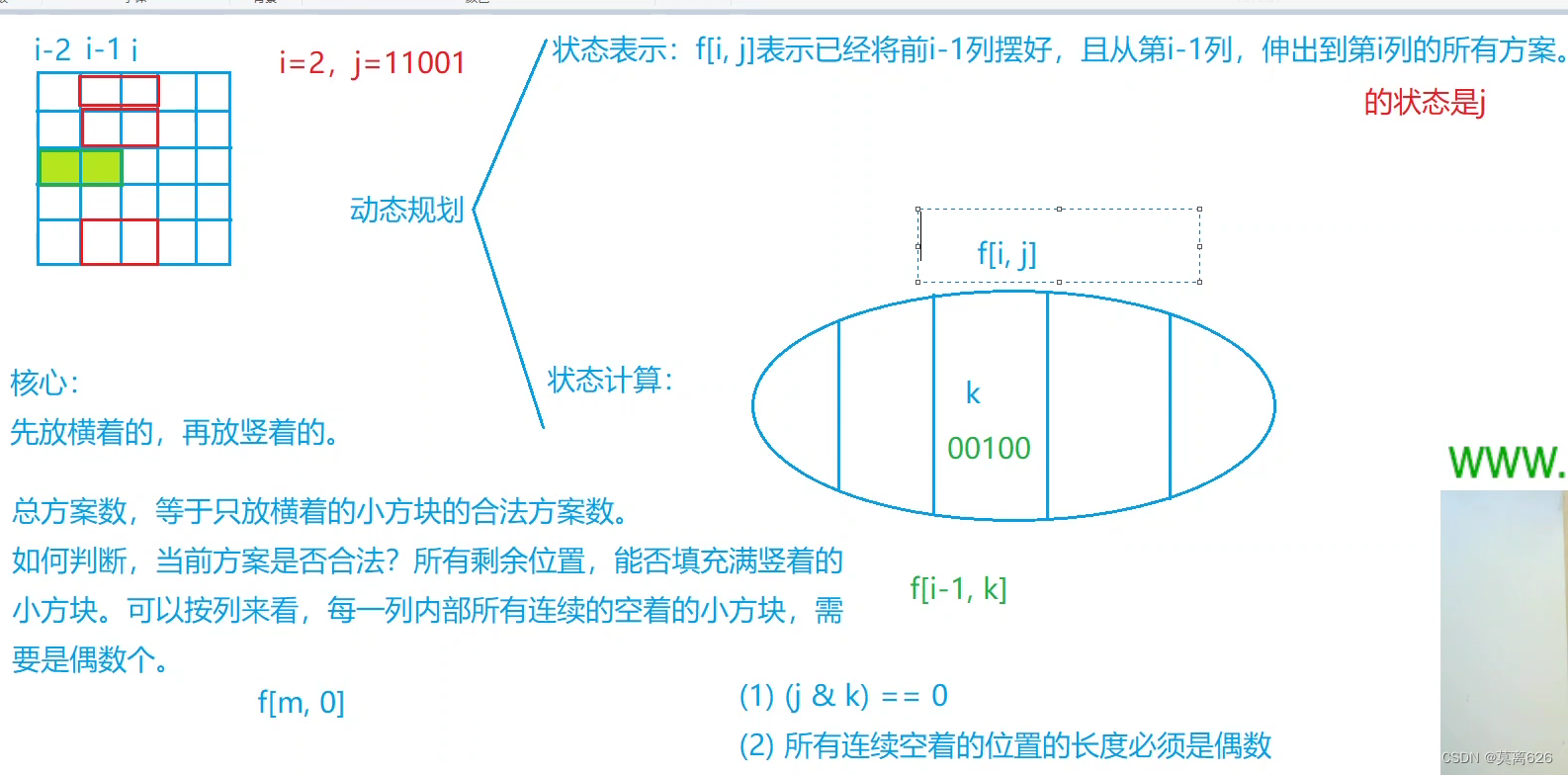
思路: 我们先预处理出来0 ~ (1 << n ) 之间的所有的合法的数;
合法的数是:二进制表示中的连续的0的个数是偶数 ;
我们开一个st 数组去表示这个数是否合法, 合法为true ,不合法为false , 之后我们利用一个vector二维动态数组 , vaild[i] 数组存储的是我们的与i相匹配的数, 哪些数与i相匹配呢? :
1. j & i == 0 : 表示i 与 j 的二进制表示下同一位不同时为1 ;
2. st[j | i ] == true : 表示我们的 i | j 是一个合法的状态 ;
之后, 每个vaild[i] 数组存储的就是能跟i这个数所匹配的那些数了。
之后我们进行状态转移即可。
并且 初始化 f[0][0] = 1 , 表示我们从第 -1 列, 伸到第0列且状态是0的所有的方案不难知道这种的方案是1 。
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
typedef long long LL ;
const int N = 12 , M = 1 << N ;
int n , m ;
LL f[N][M] ;
bool st[M] ;
vector<int> valid[M] ;
int main()
{
while(cin >> n >> m , n | m )
{
// 这一部分就是一个预处理,我们去实现对于每一个数得出这个数的合法的与这个数合法的其他数。
// "*************这个遍历的是我们求得的对于在0 ~ (1 << n ) 之间 的所有的数的连续的0是否是偶数位 , 如果是偶数位就代表该数是一个合法的状态****************"
for(int i = 0 ; i < 1 << n ; i ++ )
{
int cnt = 0;
st[i] = true ;
for(int j = 0 ; j < n ; j ++ )
{
if(i >> j & 1 )
{
if(cnt & 1 )
{
st[i] = false ;
break ;
}
cnt = 0 ;
}
else cnt ++ ;
}
if(cnt & 1 ) st[i] = false ;
}
// "******************************"
for(int i = 0 ; i < 1 << n; i ++ ) // 开始寻找0 ~ (1 << n ) 每一个 之间的每一个数的能被另一个数转移过来的另一个数。
{
valid[i].clear() ;
for(int j = 0; j < 1 << n ; j ++ )
{
if((i & j ) == 0 && st[i | j] )
{
valid[i].push_back(j) ;
}
}
}
memset(f , 0 , sizeof f ) ;
f[0][0] = 1;
for(int i = 1; i <= m ; i ++ )
{
for(int j = 0 ; j < 1 << n; j ++ )
{
for(auto k : valid[j] )
{
f[i][j] += f[i - 1][k] ;
}
}
}
cout << f[m][0] << endl ;
}
return 0;
}
思路:直接上大佬的 题解
#include <iostream>
#include <cstring>
using namespace std ;
const int N = 20 , M = 1 << 20 ;
int weight[N][N] ;
int n ;
int f[M][N] ; // f[i][j] i在二进制的表示下代表某些点是否被选, 并且停在j的最短路径。
int main()
{
cin >> n ;
for(int i = 0 ; i < n ; i ++ ) // 注意这里要从0 开始读取, n 对应的是 n - 1
{
for(int j = 0 ; j < n ; j ++ )
{
cin >> weight[i][j] ;
}
}
memset(f , 0x3f , sizeof f ) ;
f[1][0] = 0 ;
for(int i = 0 ; i < (1 << n) ; i ++ )
{
for(int j = 0 ; j < n ; j ++ )
{
if(i >> j & 1 )
{
for(int k = 0 ; k < n ; k ++ )
{
if(i - (1 << j ) >> k & 1 )
{
f[i][j] = min(f[i][j] , f[i - (1 << j)][k] + weight[k][j] );
}
}
}
}
}
cout << f[(1 << n) - 1][n - 1] << endl ;
return 0 ;
}
思路: 大佬题解
需要注意的点:
1.对于代码中的这个代码块
if((a & b) == 0 ) // 为什么我们写成 !(a & b )
{
head[i].push_back(j) ;
}
需要注意的是这个条件当中我们要对这个a & b 加上一个括号 再进行判断, 注意哦 优先级 : == 大于 &
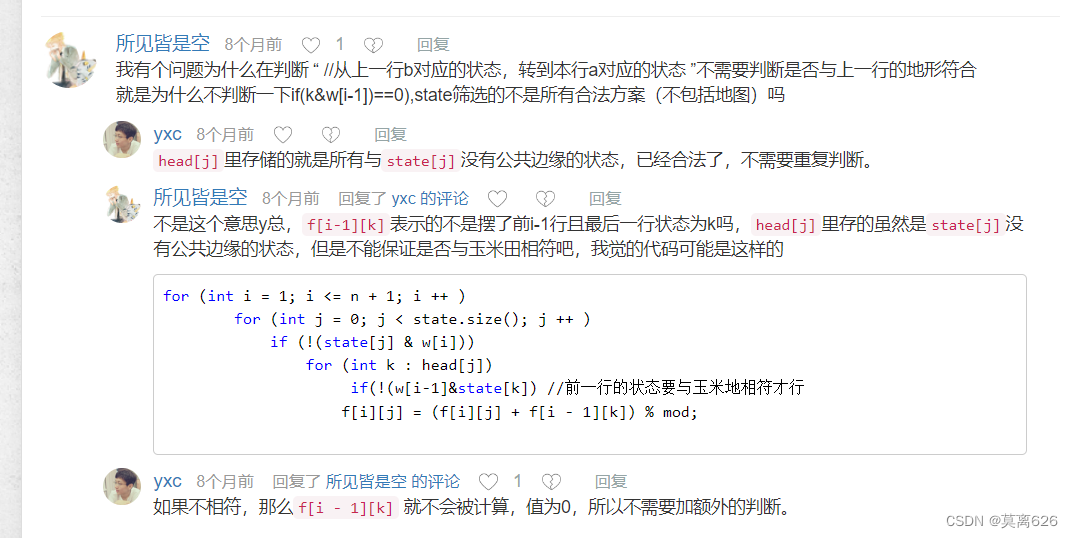
注意我们根据第i行的状态枚举的第 i - 1 行的状态(也就是说这两个状态一定不冲突)在本题中并没有判断这个第 i - 1行的状态是否合法 ,但这个状态(也就是代码中的k下标所对应的状态)的值也就是 f[i -1][k] 等于0即使我们加上之后我们也没有什么变化, 所以这里不影响;
代码 :
// 代码1 :
#include <iostream>
#include <vector>
using namespace std ;
typedef long long LL ;
const int N = 14 , M = 1 << 12 , mod = 1e8 ;
int n , m ;
LL f[N][M] ; // 前i行并且第i行种植状态是j 的情况下方案数。
// 如果上一行的 j 列种植了作物, 那么这一行的 j 列就不能种植作物 。 也就是说 a & b == 0 , 如何求 a所对应的我们的合法的状态呢
vector<int> state ; // 先找到所有的1不连续的所有的合法的状态 。
vector<int> head[M] ;
int g[N] ;
bool check(int x ) // 判断一个数的二进制表示下是否存在连续的1
{
for(int i = 0 ; i + 1 < m ; i ++ )
{
if(x >> i & 1 && x >> (i + 1) & 1 ) return false ;
}
return true ;
}
int main()
{
cin >> n >> m ; // n 行 m 列
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = m - 1 ; j >= 0 ; j -- )
{
int t ;
cin >> t ;
g[i] += !t * (1 << j ) ;
}
}
// g[i] 的二进制表示下表示若某一位为1 则表示这个位置不能种玉米
for(int i = 0 ; i < (1 << m) ; i ++ )
{
if(check(i))
{
state.push_back(i) ;
}
}
// for(int i = 0 ; i < state.size() ; i ++ ) cout << state[i] << ' ';
for(int i = 0 ; i < state.size() ; i ++ )
{
for(int j = 0 ; j < state.size() ; j ++ )
{
int a = state[i] , b = state[j] ;
if((a & b) == 0 ) // 为什么我们写成 !(a & b )
{
head[i].push_back(j) ;
}
}
}
f[0][0] = 1;
for(int i = 1 ; i <= n + 1 ; i ++ )
{
for(int j = 0 ; j < state.size() ; j ++ )
{
if((state[j] & g[i] ) == 0 ) // 表明 state[j] 这个种植方式能够在第i行进行一个种植。
{
for(auto k : head[j])
{
f[i][j] = (f[i][j] + f[i - 1][k]) % mod ;
}
}
}
}
cout << f[n + 1][0] << endl ;
return 0 ;
}
// 代码2 :
#include <iostream>
#include <vector>
using namespace std ;
typedef long long LL ;
const int N = 14 , M = 1 << 12 , mod = 1e8 ;
int n , m ;
LL f[N][M] ; // 前i行并且第i行种植状态是j 的情况下方案数。
// 如果上一行的 j 列种植了作物, 那么这一行的 j 列就不能种植作物 。 也就是说 a & b == 0 , 如何求 a所对应的我们的合法的状态呢
vector<int> state ; // 先找到所有的1不连续的所有的合法的状态 。
vector<int> head[M] ;
int g[N] ;
bool check(int x ) // 判断一个数的二进制表示下是否存在连续的1
{
for(int i = 0 ; i + 1 < m ; i ++ )
{
if(x >> i & 1 && x >> (i + 1) & 1 ) return false ;
}
return true ;
}
int main()
{
cin >> n >> m ; // n 行 m 列
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = m - 1 ; j >= 0 ; j -- )
{
int t ;
cin >> t ;
g[i] += !t * (1 << j ) ;
}
}
// g[i] 的二进制表示下表示若某一位为1 则表示这个位置不能种玉米
for(int i = 0 ; i < (1 << m) ; i ++ )
{
if(check(i))
{
state.push_back(i) ;
}
}
for(int i = 0 ; i < state.size() ; i ++ )
{
for(int j = 0 ; j < state.size() ; j ++ )
{
int a = state[i] , b = state[j] ;
if((a & b) == 0 ) // 为什么我们写成 !(a & b )
{
head[a].push_back(b) ;
}
}
}
f[0][0] = 1;
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = 0 ; j < state.size() ; j ++ )
{
if((state[j] & g[i] ) == 0 ) // 表明 state[j] 这个种植方式能够在第i行进行一个种植。
{
for(auto k : head[state[j]])
{
f[i][state[j]] = (f[i][state[j]] + f[i - 1][k]) % mod ;
}
}
}
}
LL ans = 0 ;
for(int i = 0 ; i < state.size() ; i ++ ) ans = (ans + f[n][state[i]]) % mod ;
cout << ans << endl ;
return 0 ;
}
区间dp
这题的对于我的难点:
1.在使用高精度的时候我们也可以使用数组去模拟高精度的乘积与加和, 因为这样的话我们可以使用memcpy函数, 从而直接存储在原来的位置上,我们就不需要再开新的变量去存储这个东西了。
2.在这个题当中, 有一个技巧也需要注意,看这一小段:
memset(temp , 0 , sizeof temp ) ;
temp[0] = w[j] ;
mul(temp , w[i] ) ;
这个时候,我们的temp数组存储的是即将参加高精乘的数字,但这里我们直接将w[j]这整个数直接存储在temp数组的第一个位置上了, 这样能够简化一些代码, 但注意的是一旦使用了这个技巧, 在mul()函数中,我们就需要去将 t t t的类型开为 l o n g l o n g long long longlong 类型的了。
#include <cstring>
#include <vector>
#include <iostream>
using namespace std ;
typedef long long LL ;
const int N = 55 , M = 35 ;
LL f[N][N][M] ;
LL w[N] ;
LL n ;
void mul(LL a[] , LL b )
{
LL c[M] ;
LL t = 0 ;
for(int i = 0 ; i < M ; i ++ )
{
t += a[i] * b ;
c[i] = t % 10 ;
t /= 10 ;
}
memcpy(a , c , sizeof c ) ; // 我们这里这样写的好处就是少定义了很多的变量。
}
void add(LL a[] , LL b[] )
{
LL c[M] ;
int t = 0 ;
for(int i = 0 ; i < M ; i ++ )
{
t += a[i] + b[i] ;
c[i] = t % 10 ;
t /= 10 ;
}
memcpy(a , c , sizeof c) ;
}
void print(LL a[] )
{
int k = M - 1 ;
while(k && !a[k] ) k -- ;
while(k >= 0 ) cout << a[k -- ] ;
cout << endl ;
}
int cmp(LL a[] , LL b[] )
{
for(int i = M - 1 ; i >= 0 ; i -- )
{
if(a[i] > b[i] ) return 1 ;
else if(a[i] < b[i] ) return -1 ;
}
return 0 ;
}
int main()
{
cin >> n ;
for(int i = 1; i <= n ; i ++ ) cin >> w[i] ;
LL temp[M] ;
for(int len = 3 ; len <= n ; len ++ )
{
for(int i = 1; i + len - 1 <= n ; i ++ )
{
int k = i + len - 1 ;
f[i][k][M - 1] = 1 ;
for(int j = i + 1 ; j < k ; j ++ )
{
memset(temp , 0 , sizeof temp ) ;
temp[0] = w[j] ;
mul(temp , w[i] ) ;
mul(temp , w[k] ) ;
add(temp , f[i][j] ) ;
add(temp , f[j][k] ) ;
if(cmp(f[i][k] , temp ) > 0 )
{
memcpy(f[i][k] , temp , sizeof temp ) ;
}
}
}
}
print(f[1][n] ) ;
return 0 ;
}``






















 563
563











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








